A block is placed on a rough horizontal plane. A time-dependent horizontal force F=kt2 acts on the block. Here k is a positive constant. Acceleration -time graph of the block is
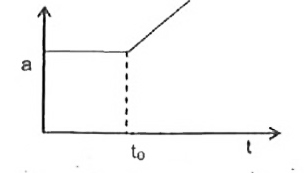
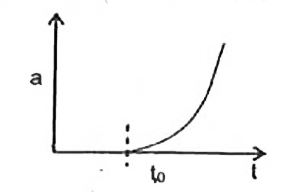
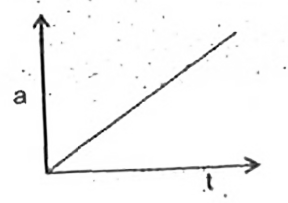
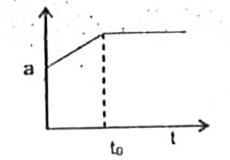
The correct Answer is:B
To solve the problem, we need to analyze the given force acting on the block and determine the acceleration as a function of time. The force is given as F=kt2, where k is a positive constant.
1. Identify the relationship between force, mass, and acceleration:
According to Newton's second law, the force acting on an object is equal to the mass of the object multiplied by its acceleration:
F=ma
Here, F is the force, m is the mass of the block, and a is its acceleration.
2. Substitute the expression for force:
We know that F=kt2. Substituting this into the equation gives:
kt2=ma
3. Solve for acceleration:
Rearranging the equation to solve for acceleration a:
a=kt2m
Here, km is a constant since both k and m are constants.
4. Identify the form of the acceleration function:
The expression a=kmt2 indicates that acceleration is proportional to the square of time t2. This means that the graph of acceleration versus time will be a quadratic function.
5. Determine the shape of the graph:
Since the coefficient km is positive (as both k and m are positive), the graph of acceleration as a function of time will be a parabola opening upwards.
Conclusion:
The acceleration-time graph of the block will be a parabola that opens upwards, indicating that as time increases, the acceleration increases quadratically.
According to Newton's second law, the force acting on an object is equal to the mass of the object multiplied by its acceleration:
F=ma
Here, F is the force, m is the mass of the block, and a is its acceleration.
We know that F=kt2. Substituting this into the equation gives:
kt2=ma
Rearranging the equation to solve for acceleration a:
a=kt2m
Here, km is a constant since both k and m are constants.
The expression a=kmt2 indicates that acceleration is proportional to the square of time t2. This means that the graph of acceleration versus time will be a quadratic function.
Since the coefficient km is positive (as both k and m are positive), the graph of acceleration as a function of time will be a parabola opening upwards.
The acceleration-time graph of the block will be a parabola that opens upwards, indicating that as time increases, the acceleration increases quadratically.
Topper's Solved these Questions
- LAWS OF MOTIONBook:FIITJEEChapter:LAWS OF MOTIONExercise:ASSIGNMENT PROBLEMS (OBJECTIVE)(Level-1) (ASSERTION REASONING TYPE)
Explore 2 Videos
- LAWS OF MOTIONBook:FIITJEEChapter:LAWS OF MOTIONExercise:ASSIGNMENT PROBLEMS (OBJECTIVE) (Level-II)
Explore 23 Videos
- LAWS OF MOTIONBook:FIITJEEChapter:LAWS OF MOTIONExercise:ASSIGNMENT PROBLEMS (SUBJECTIVE) (Level-II & III)
Explore 18 Videos
- KINEMATICSBook:FIITJEEChapter:KINEMATICSExercise:NUMERICAL BASED QUESTIONS DECIMAL TYPE
Explore 5 Videos
- MAGNETICBook:FIITJEEChapter:MAGNETICExercise:Numerical Based Type
Explore 2 Videos
Similar Questions
A block of mass 4kg is placed on a rough horizontal plane A time dependent horizontal force F=kt acts on the block (k=2N/s). Find the frictional force between the block and the plane at t=2 seconds and t=5 seconds (μ=0.2) .
View SolutionA block of mass 5kg is placed on a rough horizontal plane.A time dependent horizontal force F=(t2+2t) N acts on the block. The friction force between the block and the plane at t=3s is (μ=0.4)
View Solution
Knowledge Check
A block is placed on a rough horizontal plane. A time dependent horizontal force F=K t acts on the block K is a postive constant. Accelration-time graph of the block is
A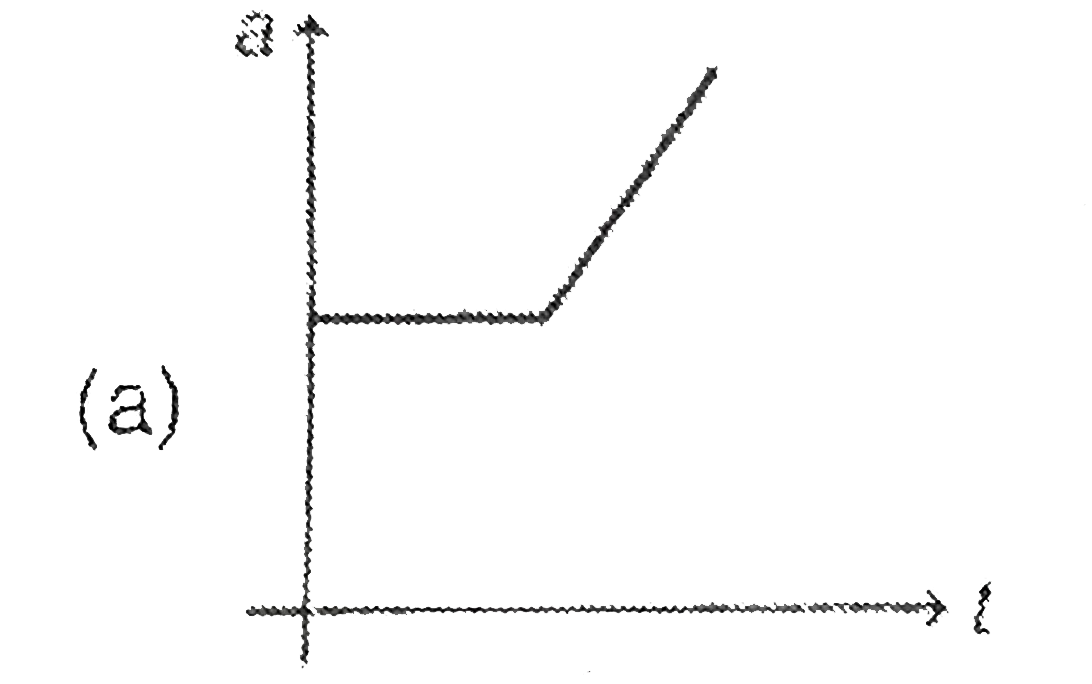 B
B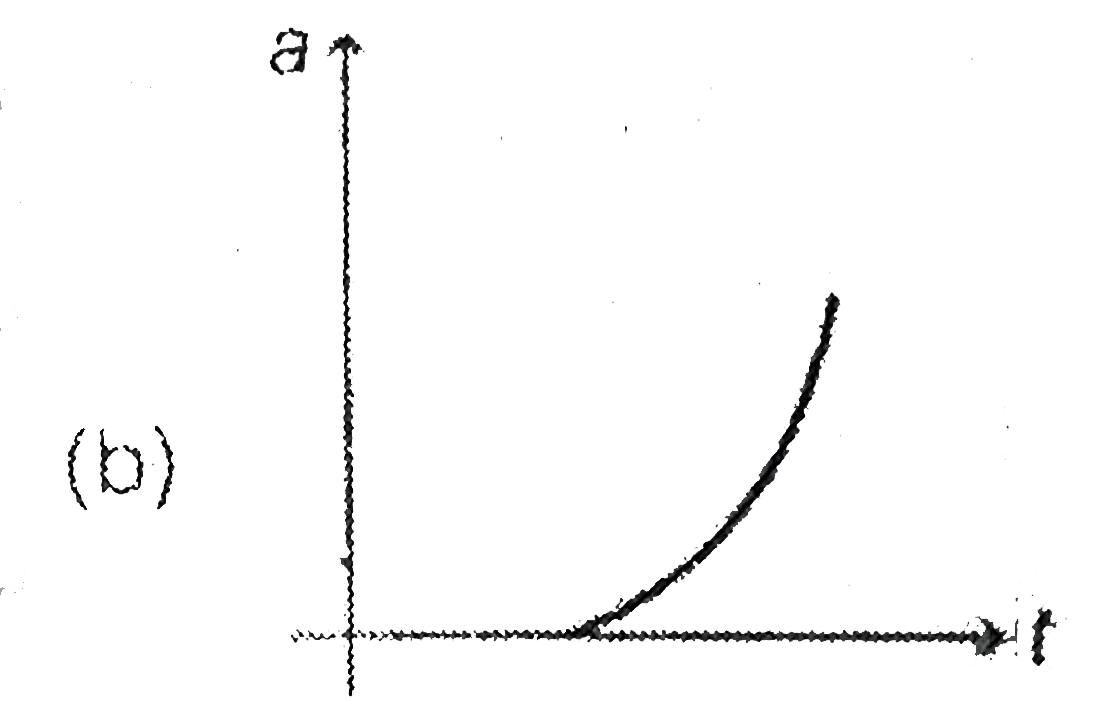 C
C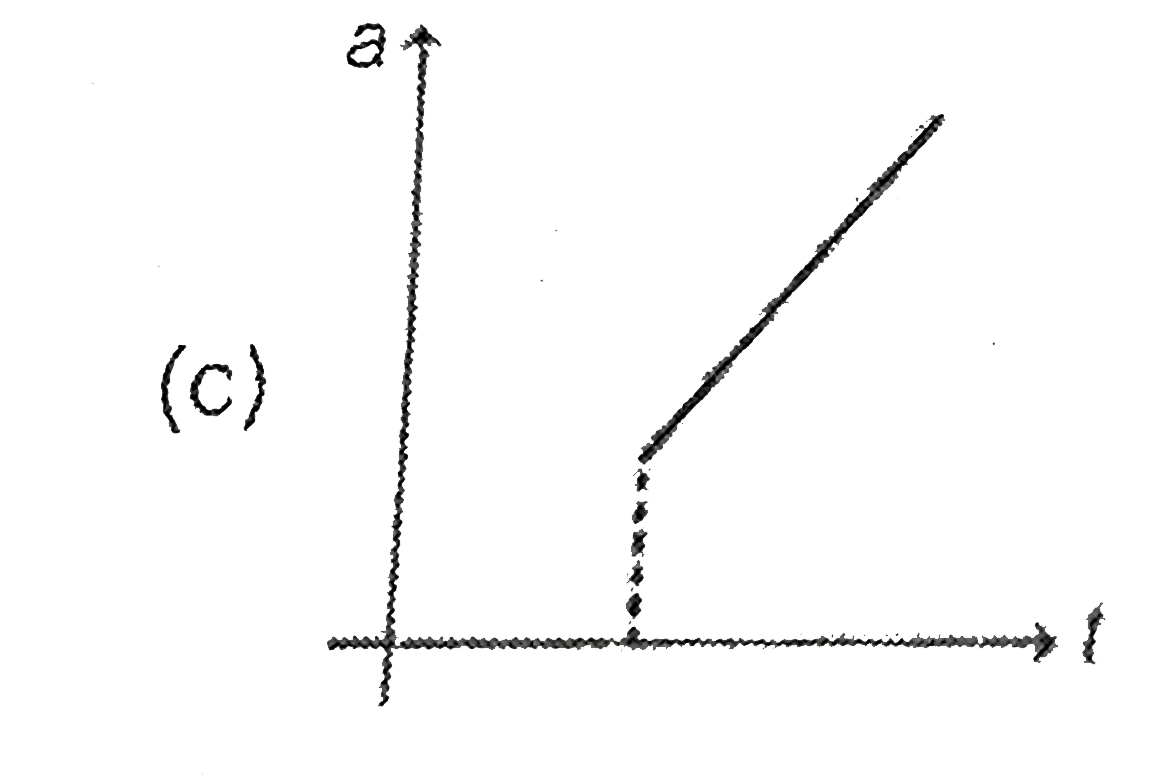 D
D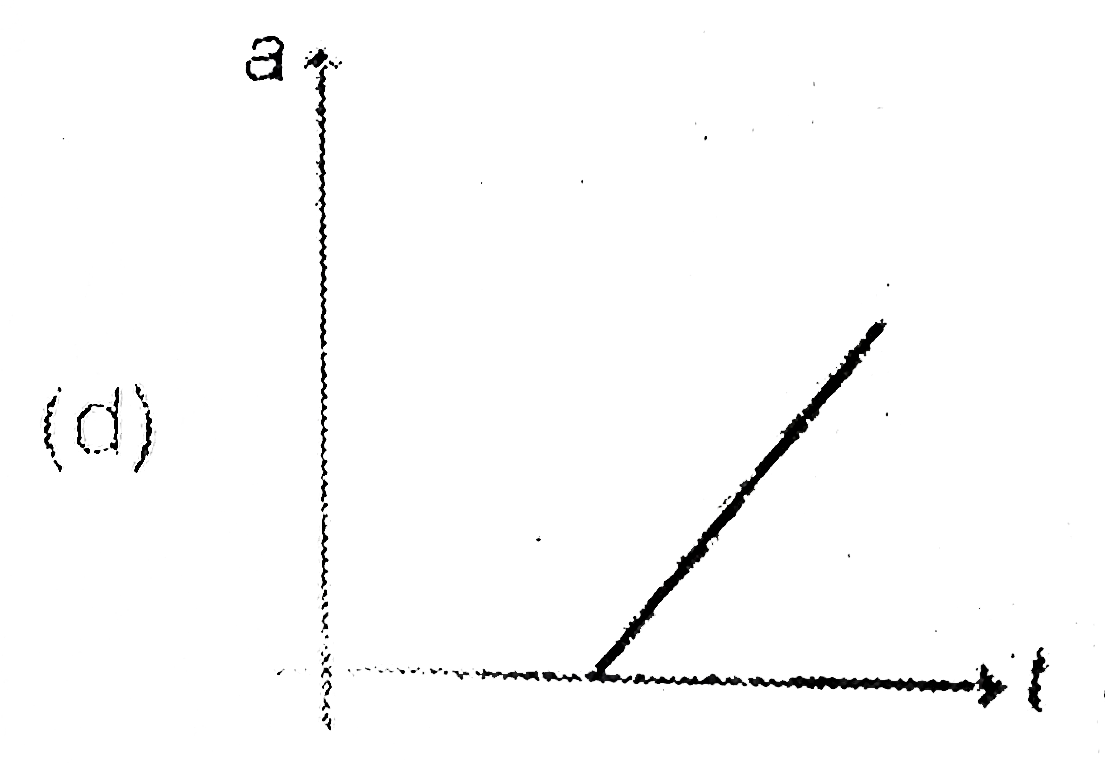
A block of mass 4kg is placed on a rough horizontal force plane. A time dependent horizontal force F=kt acts on the block. Here k=2Ns−1. The frictional force between the block and plane at time t=2s is (μ=0.2)
A4NB8NC12ND10NA block of mass 8 kg is placed on a rough horizontal plane. A time dependent force F=kt2acts on the block, where k=3N/s2. Coefficient of friction is0.6. Force of friction between the block and the plane at t=1s is
A48NB4NC2ND3N
A block is placed on a rough horizontal plane. Three horizontalforces are applied on the block as shown in the figure. If the block is in equilibrium, find the friction force acting on the block.
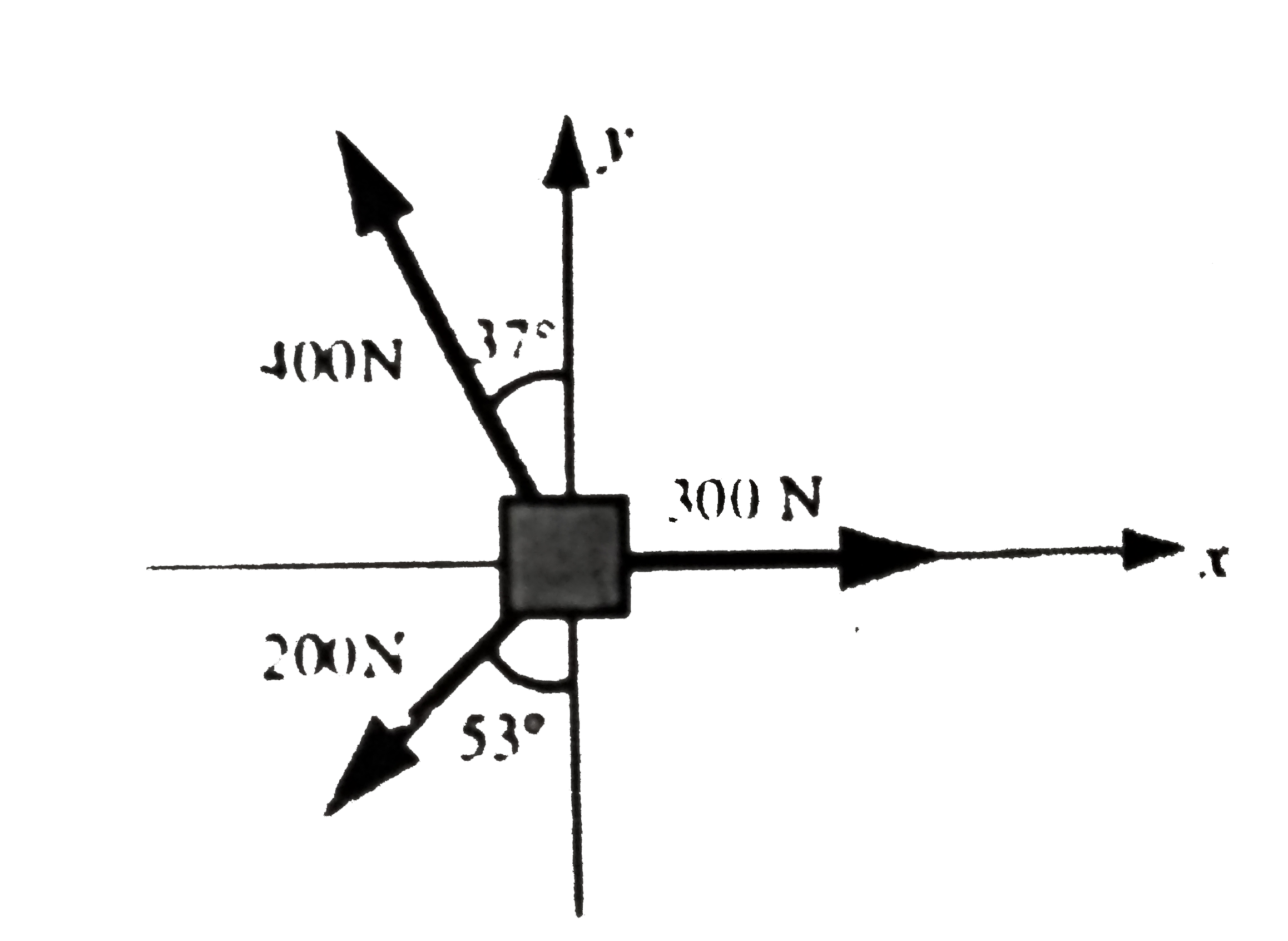
View SolutionA block is placed on a smooth inclined plane as shown . For what value of horizontal force F, the block will remain at rest ?

View SolutionA block of mass 4kg is placed on a rough horizontal plane A time dependent force F=kt2 acts on the block where k=2N/s2 Coefficient of friction μ=0.8 force of friction between the block and the plane at t=2s is
View SolutionA block of unknown mass is at rest on a rough, horizontal surface. A horizontal force F is applied to the block. The graph in the figure shows the acceleration of the block with respect to the applied force. The mass of the block is

View SolutionA block is kept on a rough horizontal surface. A variable horizontal force is acting on the block as shown in the figure. At t=0, block is at rest. Kinectic energy of block at t=5sec will be (g=10m/s2)
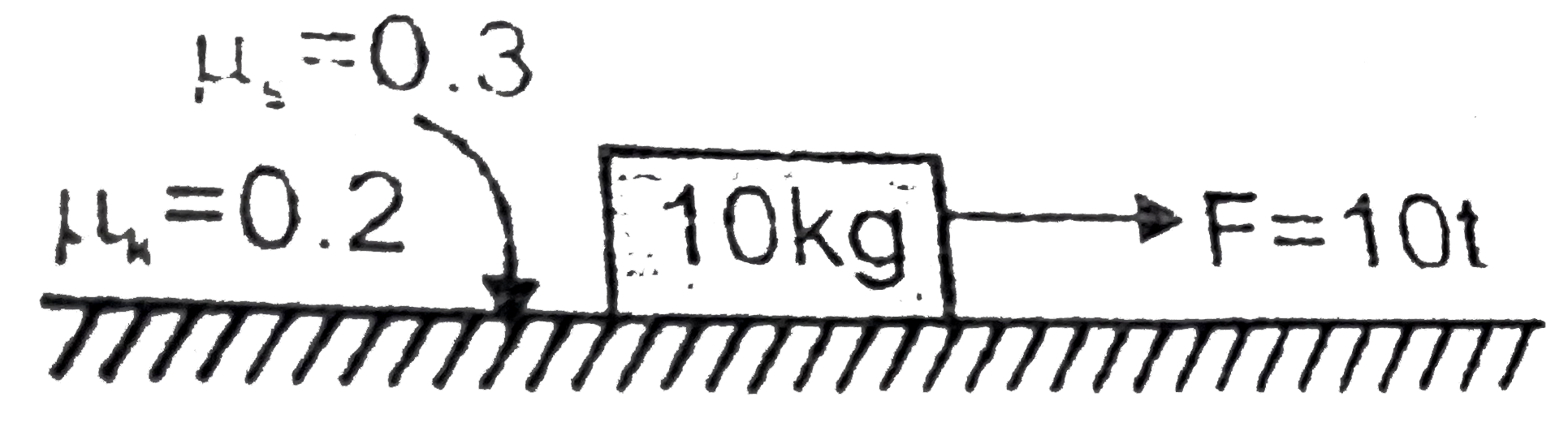
View Solution

