A smooth wedge with elevation θ is fixed in an elevator moving up with uniform acceleration a0=g/2. The base of the wedge has a length L. Find the time taken by a particle sliding down the incline to reach the base.
The correct Answer is:√16L3√3g
To solve the problem of a particle sliding down a smooth wedge fixed in an elevator moving upward with uniform acceleration, we can follow these steps:
Step 1: Understand the Forces Acting on the Particle
When the wedge is in an elevator accelerating upwards with acceleration a0=g2, we need to consider the forces acting on the particle. The forces include:
- The gravitational force mg acting downwards.
- A pseudo force ma0 acting downwards due to the upward acceleration of the elevator.
Step 2: Resolve Forces Along the Incline
The incline makes an angle θ with the horizontal. We can resolve the gravitational force and the pseudo force into components along the incline and perpendicular to the incline.
- The component of gravitational force along the incline:
Fgravity, incline=mgsinθ
- The component of pseudo force along the incline:
Fpseudo, incline=ma0sinθ=m(g2)sinθ
Step 3: Calculate the Net Force Along the Incline
The net force acting along the incline is the sum of the two components:
Fnet=mgsinθ+m(g2)sinθ=m(g+g2)sinθ=m(3g2)sinθ
Step 4: Determine the Acceleration of the Particle
Using Newton's second law, F=ma, we can find the acceleration a of the particle along the incline:
ma=m(3g2)sinθ⟹a=3g2sinθ
Step 5: Relate the Length of the Wedge to the Distance Traveled
The length of the base of the wedge is L. The distance s traveled by the particle along the incline can be related to the base length L using the geometry of the triangle formed by the wedge:
s=Lcosθ
Step 6: Use Kinematic Equation to Find Time
We can use the kinematic equation:
s=ut+12at2
Since the particle starts from rest, u=0:
s=12at2⟹t2=2sa
Substituting s=Lcosθ and a=3g2sinθ:
t2=2(Lcosθ)3g2sinθ=4L3gsinθcosθ
Step 7: Calculate Time
Taking the square root to find t:
t=√4L3gsinθcosθ=2√L√3gsinθcosθ
Step 8: Substitute for Specific Angle
If θ=30∘:
- sin30∘=12
- cos30∘=√32
Substituting these values:
t=2√L√3g(12)(√32)=2√L√3g4=2√L⋅2√3g=4√L√3g
Final Result
Thus, the time taken by the particle to slide down the incline to reach the base is:
t=4√L√3g
When the wedge is in an elevator accelerating upwards with acceleration a0=g2, we need to consider the forces acting on the particle. The forces include:
- The gravitational force mg acting downwards.
- A pseudo force ma0 acting downwards due to the upward acceleration of the elevator.
The incline makes an angle θ with the horizontal. We can resolve the gravitational force and the pseudo force into components along the incline and perpendicular to the incline.
Fgravity, incline=mgsinθ
- The component of pseudo force along the incline:
Fpseudo, incline=ma0sinθ=m(g2)sinθ
The net force acting along the incline is the sum of the two components:
Fnet=mgsinθ+m(g2)sinθ=m(g+g2)sinθ=m(3g2)sinθ
Using Newton's second law, F=ma, we can find the acceleration a of the particle along the incline:
ma=m(3g2)sinθ⟹a=3g2sinθ
The length of the base of the wedge is L. The distance s traveled by the particle along the incline can be related to the base length L using the geometry of the triangle formed by the wedge:
s=Lcosθ
We can use the kinematic equation:
s=ut+12at2
Since the particle starts from rest, u=0:
s=12at2⟹t2=2sa
t2=2(Lcosθ)3g2sinθ=4L3gsinθcosθ
Taking the square root to find t:
t=√4L3gsinθcosθ=2√L√3gsinθcosθ
If θ=30∘:
- sin30∘=12
- cos30∘=√32
t=2√L√3g(12)(√32)=2√L√3g4=2√L⋅2√3g=4√L√3g
Thus, the time taken by the particle to slide down the incline to reach the base is:
t=4√L√3g
Topper's Solved these Questions
- LAWS OF MOTIONBook:FIITJEEChapter:LAWS OF MOTIONExercise:ASSIGNMENT PROBLEMS (OBJECTIVE) (Level - 1)
Explore 50 Videos
- LAWS OF MOTIONBook:FIITJEEChapter:LAWS OF MOTIONExercise:ASSIGNMENT PROBLEMS (OBJECTIVE)(Level-1) (ASSERTION REASONING TYPE)
Explore 2 Videos
- LAWS OF MOTIONBook:FIITJEEChapter:LAWS OF MOTIONExercise:ASSIGNMENT PROBLEMS (SUBJECTIVE) (Level-I)(Numerical)
Explore 9 Videos
- KINEMATICSBook:FIITJEEChapter:KINEMATICSExercise:NUMERICAL BASED QUESTIONS DECIMAL TYPE
Explore 5 Videos
- MAGNETICBook:FIITJEEChapter:MAGNETICExercise:Numerical Based Type
Explore 2 Videos
Similar Questions
A particle slides down a smooth inclined plane of elevation θ fixed in a elevator going up with an acceleration a0. The base of the inline has a length L.
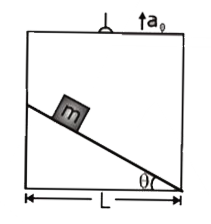
View SolutionA particle slides down a smooth in clined plane of elevation θ fixed in an elevastor going up with an accelerationa0. The base of the incline has a length L.Find the time taken by the particle to reach the bottom.
View Solution
Knowledge Check
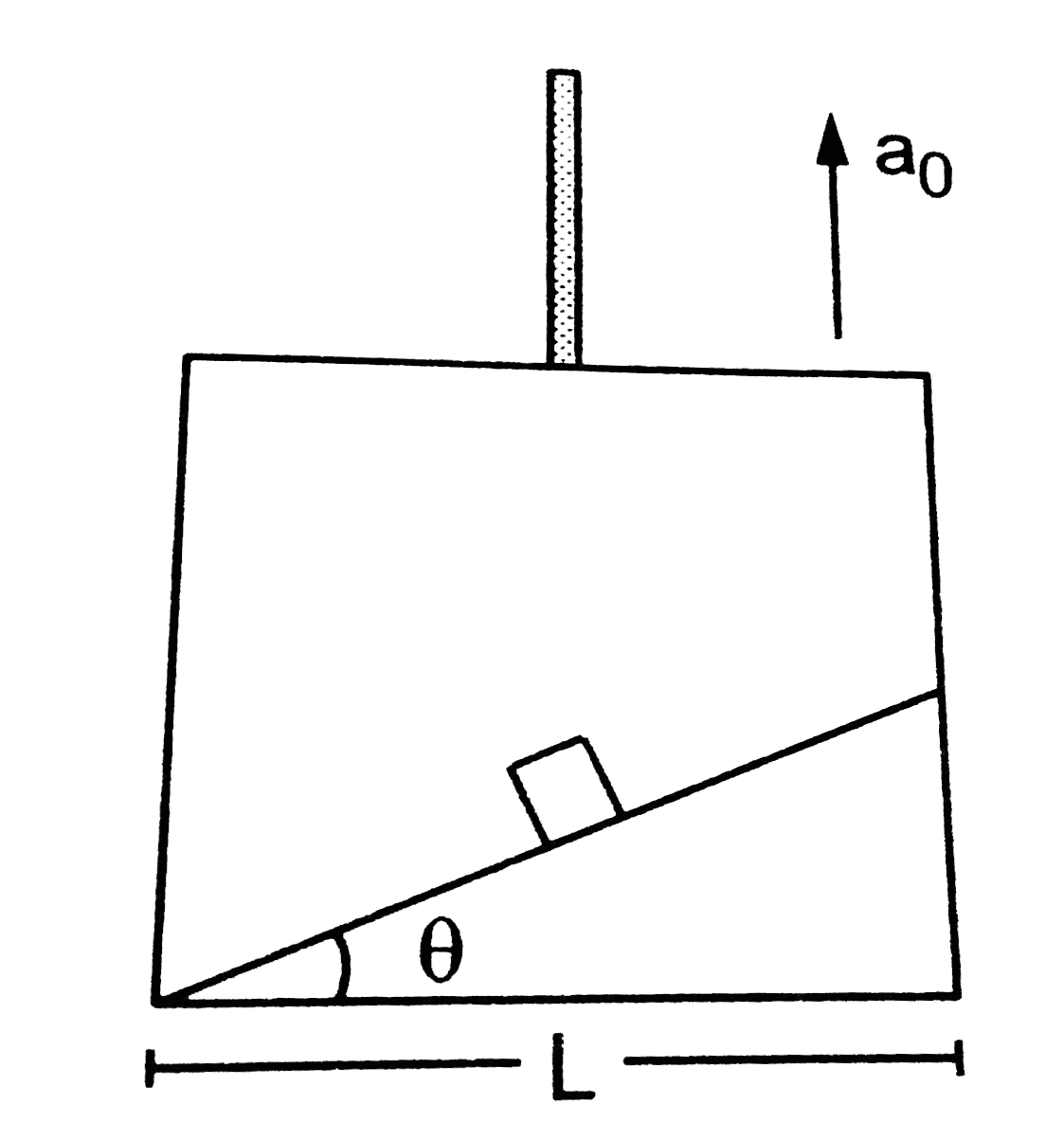
A particle slides down a smooth inclined plane of elevation , fixed in an elevator going up with an acceleration a0 (figure). The base of the incline has a length L. Find the time taken by the particle to reach to the bottom -
 A[2Lgsinθcosθ]1/2B[2L(g−a0)sinθcosθ]1/2C[2L(g+a0)cosθ]1/2D[2L(g+a0)sinθcosθ]1/2
A[2Lgsinθcosθ]1/2B[2L(g−a0)sinθcosθ]1/2C[2L(g+a0)cosθ]1/2D[2L(g+a0)sinθcosθ]1/2A particle slides down a smooth inclined plane of elevation fixed in an elevator going with an acceleration a as shown in the figure. The base of the incline has a length L.
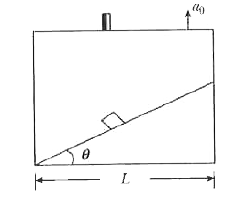
If the elevator going up with constant velocity, the time taken by the particle to reach the bottom isA(2L(gsinθcosθ))1/2B(2Lgsinθ)1/2C(2Lgcosθ)1/2DNone of theseA particle slides down on a smooth incline of inclination 30∘, fixed in an elevator going up with an acceleration 2m/s2. The box of incline has width 4m. The time taken by the particle to reach the bottom will be
 A89√3sB98√3sC43√√32sD34√√32s
A89√3sB98√3sC43√√32sD34√√32s
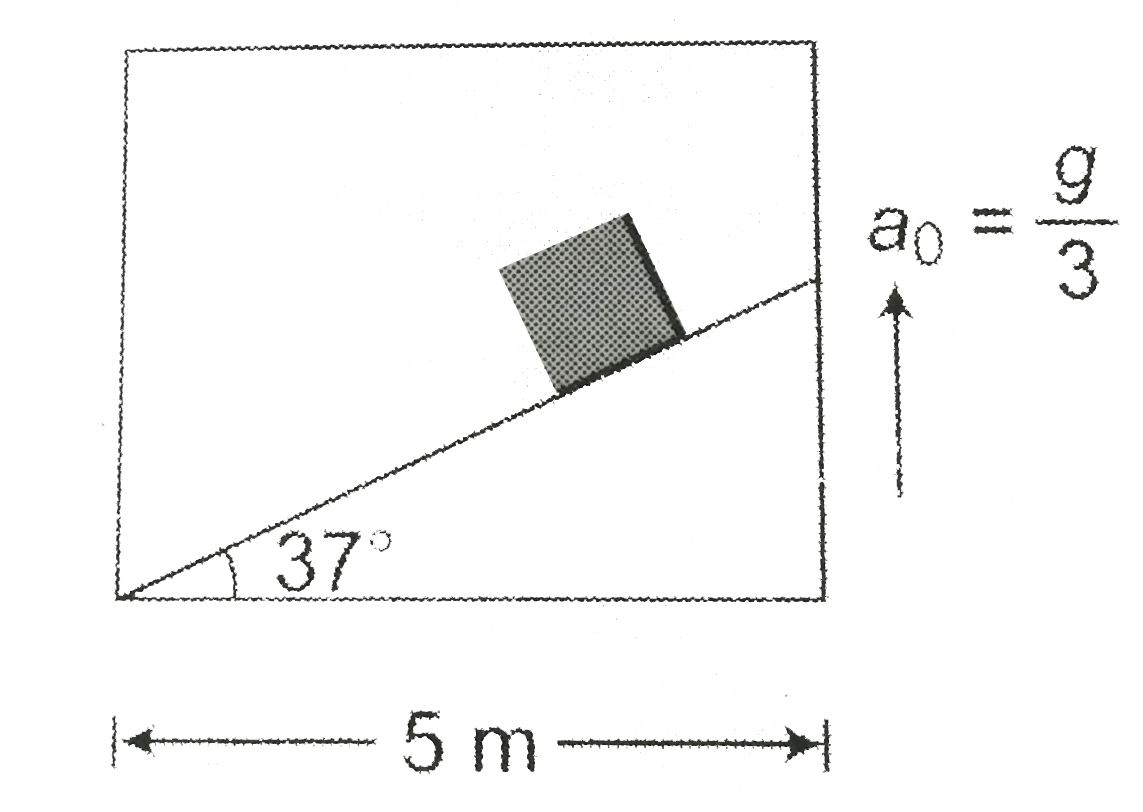
A particle slides down a smooth incline of inclination 37∘, fixed in an elevator going up with an acceleration (g)/3. The base of incline has a length 5m. Find the time taken by the particle to reach the bottom.
View SolutionA block slides down from top of a smooth inclined plane of elevation ● fixed in an elevator going up with an acceleration a0 The base of incline hs length L Find the time taken by the block to reach the bottom
 .
.
View SolutionA block is placed on an inclined plane moving towards right with an acceleration a0=g The length of the inclined plane is l0. All the surfaces are smooth Find the time taken by the block to reach from bottom to top.
 .
.
View SolutionIn the adjoining figure a wedge is fixed to an elevator moving upwards with an acceleration a. A block of mass m is placed over the wedge.Find the acceleration of the block with respect to wedge. Neglect friction

View SolutionA body of mass m is placed over a smooth inclined plane of inclination θ, which is placed over a lift which is moving up with an acceleration a0 . Base length of the inclined plane is L. Calculate the velocity of the block with respect to lift at the bottom, if it is allowed to slide down from the top of the plane from rest :-
View Solution

