In the figure shown AB, BC and PQ are thin, smooth, rigid wires. AB and AC are joined at A and fixed in vertical plane. $∠ B A C = 2 θ = 90^{\circ}$ and line AD is angle bisector of angle BAC. A liquid of surface tension T = 0.025 N/m forms a thin film in the triangle formed by intersection of the wires AB, AC and PQ. In the figure shown the uniform wire PQ of mass 1 gm is horizontal and in equilibrium under the action of surface tension and gravitational force. Find the time period of SHM of PQ in vertical plane for small displacement from its mean position, in the form $\frac{π}{X} s$ and fill value of X.

Video Solution

Text Solution

Verified by Experts

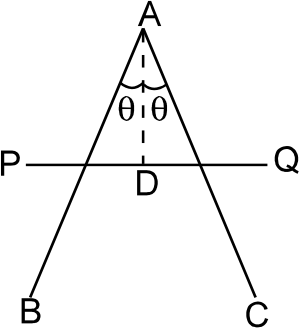
The F.B.D. of wire PQ is
The force due to surface tension $F_{S T} = 2 T \times 2 A D tan θ$

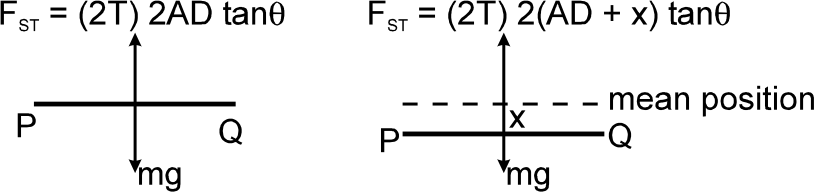
for wire to be in equilibrium (figure(a))
$4 T A D tan θ = m g ... . . (1)$
If the wire PQ is at a distance x below the mean position, the restoring force on the wire is (figure (b))
$- m a = 4 T tan θ (A D + x) - m g = 4 T tan θ x$
Hence the wire PQ executes SHM
$a = - \frac{4 T}{m} tan θ x$
comparing with a $= - ω^{2} x$ we get
$ω^{2} = \frac{4 T}{m} tan θ$
or $T = 2 π \sqrt{\frac{m}{4 T tan θ}} = 2 π \sqrt{\frac{1 \times 10^{- 3}}{4 \times 25 \times 10^{- 3}}} = \frac{π}{5} s$

Updated on:21/07/2023

In figure AD is the bisector of $∠ B A C .$ If $B D = 2 c m, C D = 3 c m and A B = 5 c m$ . Find AC :

A6 cm
B7.5 cm
C10 cm
D15 cm
Let AD be the angle bisector of $∠ A$ of $Δ A B C$ such that $A D = α A B + β A C,$ then
A $α = \frac{| A B |}{| A B | + | A C |}, β = \frac{| A C |}{| A B | + | A C |}$
B $α = \frac{| A B | + | A C |}{| A B |}, β = \frac{| A B | + | A C |}{| A C |}$
C $α = \frac{| A C |}{| A B | + | A C |}, β = \frac{| A B |}{| A B | + | A C |}$
D $α = \frac{| A B |}{| A C |}, β = \frac{| A C |}{| A B |}$
In a $△ A B C$ . AB = 5 cm, AC = 7 cm. If AD is the angle bisector of angle A, then BD :CD is :
A25:49
B49:25
C6:1
D5:7