A sphere of density ρ falls vertically downward through a fluid of density σ. At a certain instant its velocity is u. The terminal velocity of the sphere is u0. Assuming that stokes’s law for viscous drag is applicable, the instantaneous acceleration of the sphere is found to be β(1−σρ)(1−uu0). here β is in an integer. find β.
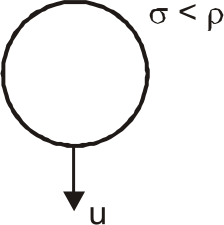
Fd=6πμru
FB=43πr3σg,mg=43πr3ρg
mg−Fd−FB=ma,u0=2r29g(ρ−σ)μ
∴A=(1−σρ)(1−uu0)g
Topper's Solved these Questions
Similar Questions
A radioactive element decays by β−emission. A detector records n beta particles in 2s and in next 2s it records 0.75n beta particles. Find mean life correct to nearest whole number. Given ln |2|=0.6931, ln |3|=1.0986.
View SolutionWhen p−n junction diode is forward biased then
View SolutionWhen a sphere falling in a viscous fluid attains a terminal velocity, then
View SolutionA sphere of radius R and density rho_1 is dropped in a liquid of density sigma . Its terminal velocity is v_1 . If another sphere of radius R and density rho_2 is dropped in the same liquid, its terminal velocity will be:
View Solutionएक प्रसारी गोले (expanding sphere) की तात्क्षणिक (instataneous) त्रिज्या R एवं द्रव्यमान M अचर रहते हैं। प्रसार के दौरान इसका तात्क्षणिक घनत्व ρ पूरे आयतन में एकसमान रहता है एंव आशिकं घनत्व की दर (1ρρpdt) अचर (constant ) है इस प्रसारी आंशिक घनत्व की दर गोले के पृष्ठ पर एक बिन्दु का वेग v निम्न के अनुक्रमानुपाती होगा :
View SolutionThe terminal velocity of a sphere of radius R, falling in a viscous fluid, is proportional to
View SolutionA sphere of density ρ is half submerged in a liquid of density σ and surface tension T. The sphere remains in equilibrium. Find radius of the sphere (assume the force due to surface tension acts tangentially to surface of sphere)
View Solutionएक गोले की त्रिज्या R तथा घनत्व ρ है। इसे σ घनत्व वाले द्रव में छोड़ा जाता है। इसका सीमान्त वेग v1 है। यदि एक अन्य गोला जिसकी त्रिज्या R तथा घनत्व ρ2 है इसी द्रव में छोड़ा जाता है, तो इसका सीमान्त वेग होगा
View Solutionसमान पदार्थ के दो गोलें जिनकी त्रिज्या R तथा 3R है, घनत्व σ के द्रव से ऊर्ध्वाधर नीचे की ओर गिराये जाते हैं। उनके सीमान्त वेगों का अनुपात हैं
View Solutionsigma and rho are surface and volume charge densities respectively of a charged sphere, so,......
View SolutionA sphere of density rho is half submerged in a liquid of density sigma and surface tension T. The sphere remains in equilibrium. Find radius of the sphere (assume the force due to surface tension acts tangentially to surface of sphere)
View SolutionDefine terminal velocity. Show that the terminal velocity υ of a sphere of radius r, density ρ falling vertically through a viscous fluid of density σ and coefficient of viscosity η is given by υ=29(ρ−σ)r2gη Use this formula to explain the observed rise of air bubbles in a liquid.
View SolutionIf rho is density of falling body and sigma is the density of fluid then the terminal velocity of the falling body is proportional to
View SolutionTwo spheres of the same material, but of radii R and 3R are allowed to fall vertically downwards through a liquid of density σ. The ratio of their terminal velocities is
View SolutionUsing Stokes' Law show that the constant terminal velocity v of a sphere of radius r, density ρ falling vertically under gravity through a viscous fluid of density σ and co-efficient of viscosity η is given by-
v=(29).[r2g(ρ−σ)η]
View Solution

