Consider a parabola $y = A x^{2} + B, - x_{0} \leq x \leq x_{0}$ .

If this curve is rotated about y axis, we get a paraboloid surface. The volume below this surface & above x–z plane is given by $V = \frac{π A x_{0}^{4}}{2} + π B x_{0}^{2} = \frac{volume of cylinder ABCD}{2} + Volume of cylinder CDEF$
Use the above result to answer following question.
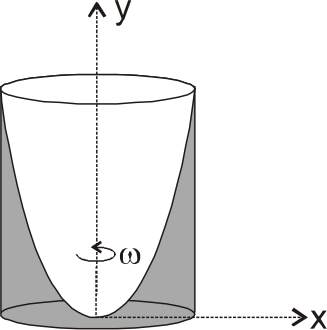
A cyllindrical container of height ‘h’ and radius ‘a’ is two-third filled. Find maximum angular velocity at which liquid can be rotated without spilling it.

$\sqrt{\frac{4 g h}{3 a^{2}}}$

$\sqrt{\frac{2 g h}{3 a^{2}}}$

$\sqrt{\frac{g h}{a^{2}}}$

$\sqrt{\frac{g h}{2 a^{2}}}$

Video Solution

Text Solution

Verified by Experts

Profile of rotating liquids is given by

$y = \frac{ω^{2} x^{2}}{2 g}$
Putting $x = 1, y = \frac{ω^{2} a^{2}}{2 g}$
Volume of liquid in fig (b) is written as $= \frac{π a^{2} \times \frac{ω^{2} a^{2}}{2 g}}{2} + π a^{2} (h - \frac{ω^{2} a^{2}}{2 g})$
Equating to volume in figure (a), we get
$π a^{2} \frac{2 h}{3} = \frac{π a^{2} ω^{2} a^{2}}{4 g} + π a^{2} [h - \frac{ω^{2} a^{2}}{2 g}] \Rightarrow ω = \sqrt{\frac{4 g h}{3 a^{2}}}$

Updated on:21/07/2023

Consider a parabola $y = A x^{2} + B, - x_{0} \leq x \leq x_{0}$ .

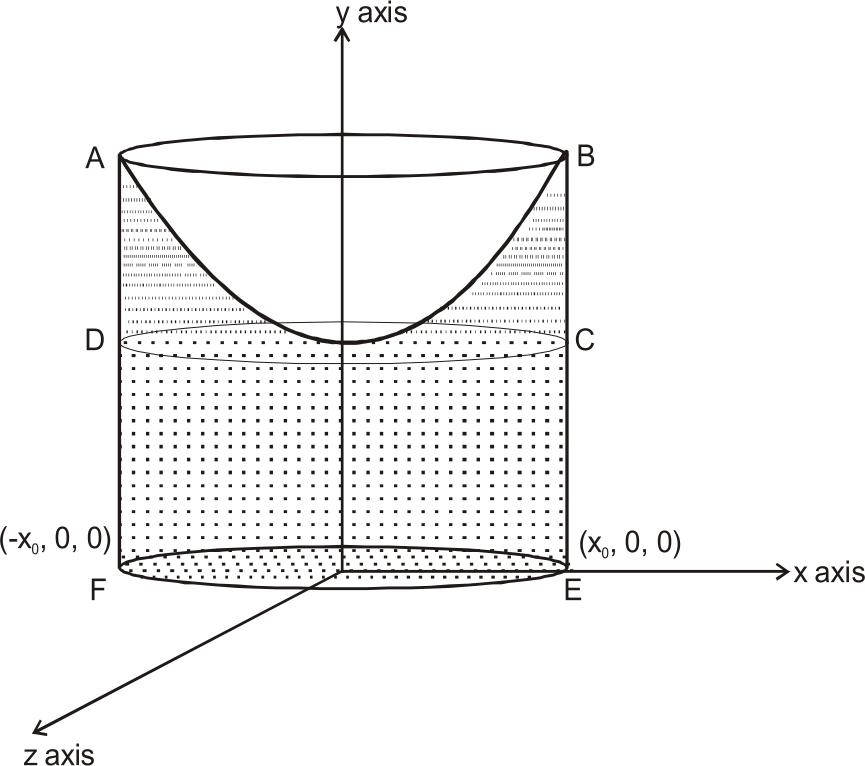
If this curve is rotated about y axis, we get a paraboloid surface. The volume below this surface & above x–z plane is given by $V = \frac{π A x_{0}^{4}}{2} + π B x_{0}^{2} = \frac{volume of cylinder ABCD}{2} + Volume of cylinder CDEF$
Use the above result to answer following question.
If the cylinder of previous problem was completely filled, then the minimum angular velocity at which base may be visible is.
A $\sqrt{\frac{g h}{a^{2}}}$
B $\sqrt{\frac{2 g h}{a^{2}}}$
C $\sqrt{\frac{g h}{2 a^{2}}}$
D $\sqrt{\frac{4}{3} \frac{g h}{a^{2}}}$
Consider a parabola $y = A x^{2} + B, - x_{0} \leq x \leq x_{0}$ .

If this curve is rotated about y axis, we get a paraboloid surface. The volume below this surface & above x–z plane is given by $V = \frac{π A x_{0}^{4}}{2} + π B x_{0}^{2} = \frac{volume of cylinder ABCD}{2} + Volume of cylinder CDEF$
Use the above result to answer following question.
In the above situation (i.e. fully filled cylinder of radius ‘a’ and height ‘h’), if liquid is rotated at twice the angular velocity found in previous problem, then the amount of liquid left (after spillage) in the cylinder will be :
A $\frac{π a^{2} h}{2}$
B $\frac{π a^{2} h}{4}$
C $\frac{π a^{2} h}{8}$
D $\frac{π a^{2} h}{3}$
The area of region between $y = 4 - x^{2}, 0 \leq x \leq 2$ and the x-axis is
A $\frac{4}{3}$
B $\frac{7}{3}$
C $\frac{16}{3}$
D $\frac{5}{3}$