Water in a clean large cuboid aquarium forms a meniscus, as shown in the figure. The difference in height between the centre and the edge of the meniscus is h. Surface tension of water is S=0.073Nm−1. Atmospheric pressure is P0=105N/m2 . Angle of contact between the water and aquarium wall is zero.
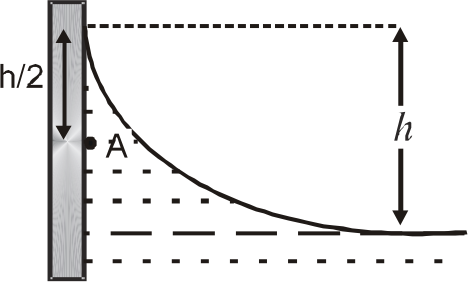
Answer the following 3 question above illustrated situation.
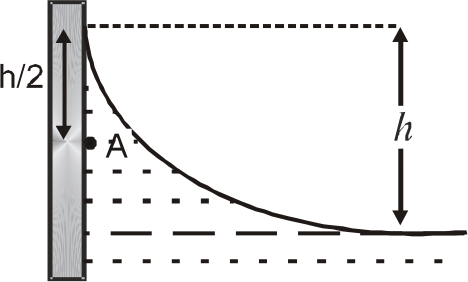
For an aquarium with side walls of length l ,horizontal force on the volume of water enclosed by the dashed line and free surface, by one aquarium wall is
(P0+ρgh2)lh
(P0−ρgh2)lh
(P0−ρgh)lh
P0lh
The pressure of the water changes linearly with the increase in height. At the bottom of the meniscus it is equal to the external atmospheric pressure p0, and at the top to . The average pressure exerted on the wall is Paverage=p0−ρgh/2. The force corresponding to this value, for an aquarium with side walls of length l, isF1=paveragelh. Consider the horizontal forces acting on the volume of water enclosed by the dashed lines in the figure. The wall pushes it to the right with force F1, the external air pushes it to the left with force F2π0lh, and the surface tension of the rest of the water pulls it to the right with a force F3=ls. The resultant of these forces has to be zero, since the volume itself is at rest. This means that
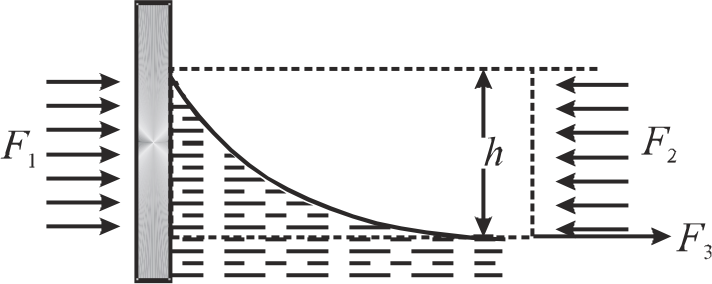
(ρ0−12ρgh)lh−p0lh+ls=0
which we can writen as
h=√2sρg=√2×0.0731000×10=0.0038m
Water rises by approximately 4 mm up the wall of the aquarium,
(ρ0−12ρgh)lh−p0lh+ls=0 which we can writen as
h=√2sρg=√2×0.0731000×10=0.0038m
Topper's Solved these Questions
Similar Questions
A radioactive element decays by β−emission. A detector records n beta particles in 2s and in next 2s it records 0.75n beta particles. Find mean life correct to nearest whole number. Given ln |2|=0.6931, ln |3|=1.0986.
View SolutionWhen p−n junction diode is forward biased then
View SolutionWater in a clean large cuboid aquarium forms a meniscus, as shown in the figure. The difference in height between the centre and the edge of the meniscus is h. Surface tension of water is S=0.073Nm−1. Atmospheric pressure is P0=105N/m2 . Angle of contact between the water and aquarium wall is zero.
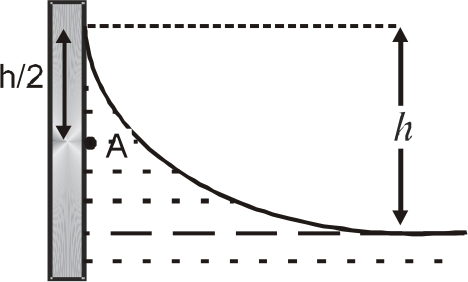
Answer the following 3 question above illustrated situation.
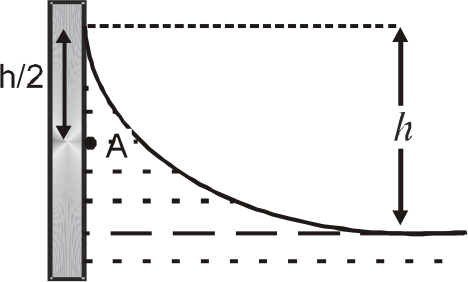
Pressure at point A is
View SolutionWater in a clean large cuboid aquarium forms a meniscus, as shown in the figure. The difference in height between the centre and the edge of the meniscus is h. Surface tension of water is S = 0.073 Nm^(-1) . Atmospheric pressure is P_0=10^5 N//m^2 . Angle of contact between the water and aquarium wall is zero. Answer the following 3 question above illustrated situation. Value of height h is
View SolutionWhile measuring surface tension of water using capillary rise method, height of the lower meniscus from free surface of water is 3cm while inner radius of capillary tube is found to be 0.5cm . Then compute surface tension of water using this data. (Take contact angle between glass and water as 0^(@) and g=9.8lms^(-2) )
View Solutionपानी पिने के एक गिलास में ऊंचाई तक पानी भरा है | पानी की ऊपरी सतह तथा पेंदे से लगी सतह पर के दाबों का अन्तर बताएँ | पानी का घनत्व =100kgm3 तथा g=10ms2
View Solutionएक r आन्तरिक त्रिज्या वाले एकसमान केशनली (uniform capillary tube) को ऊर्ध्वाधर तरीके से (vertically) पानी से भरे एक बीकर (beaker) में डुबोया जाता है। केशनली में पानी, बीकर के पानी के पृष्ठ (water surface) से, ऊंचाई h तक उठता है। पानी का पृष्ठ तनाव (surface tension) ০ है। पानी और केशनली को दीवार के बीच का सम्पर्क कोण (angle of contact) e है। मेनिस्कस (meniscus) में उपस्थित पानी के द्रव्यमान (mass) को उपेक्षा कीजिए निम्नलिखित कथनों में से कौनसा(से) सही है हैं)-
View SolutionThe figure shows a capillary tube of radius r dipped into water. The atmospheric pressure is p_0 and the capillary rise of water is h. the surface tension for water-glass is s The pressure inside water at the point A (lowest point of the ineniscus) is
View SolutionCalculate the rise of water inside a clean glass capillary tube of radius 0.1 mm when immersed in water of surface tension 7×10−2N/m. The angle of contact between water and glass is zero, density of water = 1000kg/m3,g=9.8m/s2
View SolutionThe pressure just below the meniscus of water.......
View SolutionTo what height will water in a capillary of 0.8 mm diameter rise? Assume the contact angle to be zero. If the surface tension of water is 7×10 ^ −2 N/m
View SolutionCalculate the height to which the water will rise in a capillary tube of 1.5 mm diameter (surface tension of water =74×10−3Nm−1, angle of contact between water and glass =0∘).
View SolutionWhat is the difference of pressure between the inside and outside of a spherical drop of water of radius 1mm? Surface tension of water = 7.2 xx 10^(-2)Nm^(-1)
View SolutionA spherical air bubble is formed in water at a depth of 1.2 m from the surface. The diameter of the bubble is 0.6 mm and surface tension of water is 0.073Nm−1. Calculate the pressure inside . Atmospheric pressure =10.3m of water.
View Solution
System is shown in the figure. Velocity of sphere A is 9 ms. Find the speed of sphere B.
View Solution
