Between a frame and a light slider, a thin film of soap solution is made. Whose length is x and width is y. Find surface tension force on the slider. To keep the slider in equilibrium, how much weight should be suspended ?
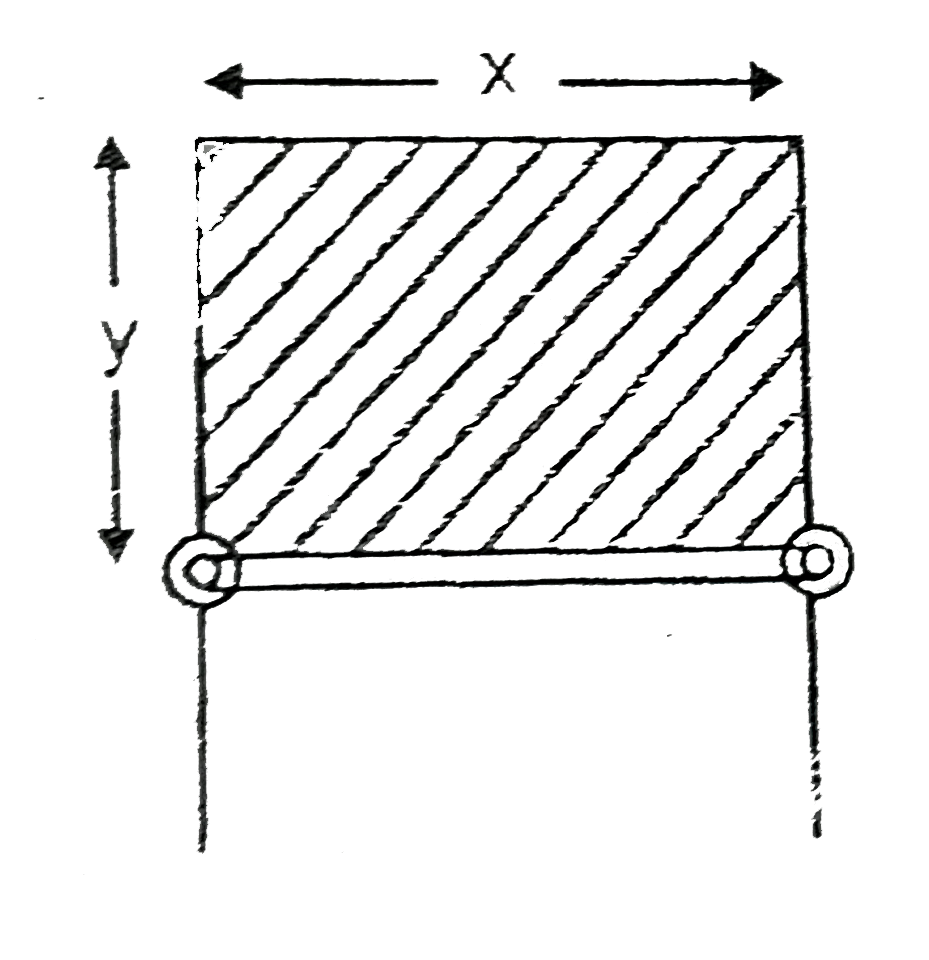

The surface will act like a tight membrane and pull the slider with a force
F=(T)(l)
Since this a film, it will have two surfaces: the front surface and the back surface. On the front surface, contact length is x, and also on the back surface contact length is x. So total contact length will be l=x+x=2x
So surface tension force on slider.
F=(T)(2x)
For equilibrium, this force will be balanced by weight of suspended block.
(T)(2x)=mg
m=2Txg
Topper's Solved these Questions
- SURFACE TENSIONBook:RESONANCEChapter:SURFACE TENSIONExercise:Exercise- 1 PART - I
Explore 10 Videos
- SURFACE TENSIONBook:RESONANCEChapter:SURFACE TENSIONExercise:Exercise- 1 PART - II
Explore 17 Videos
- STRING WAVESBook:RESONANCEChapter:STRING WAVESExercise:Exercise
Explore 32 Videos
- UNITS, DIMENSION & MEASUREMENTBook:RESONANCEChapter:UNITS, DIMENSION & MEASUREMENTExercise:Exercise
Explore 27 Videos
Similar Questions
A light wire AB of length 10 cm can slide on a vertical frame as shown in figure. There is a film of soap solution trapped between the frame and the wire. Find the load W that should be suspended from the wire to keep it in equilibrium. Neglect friction. Surface tension of soat solution =25dy≠cm−1.Takeg=10ms−2

View Solution(a) In the arrangmenet shown in the figure the frictional coefficient between the traingular wedge and floor is μ=1/√3. The frictional force is sufficient to keep the system in equilibrium.
Find how much the normal reaction between the wedge and floor is displaced from the centre of mass of wedge. All other surface are frictionless. Assume masses of both the bodies same and equal to m. Radius of sphere =R, length of side of triangular wedge d =3√3R.
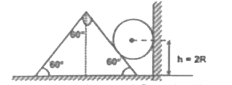
( b) If the surface of contact between the floor & the wedge also becomes frictionless, the find the speed of both bodies when sphere hits the ground. Initial height of centre of mass of sphere = 2R as shown.
View Solution
Knowledge Check
A thin liquid film formed between a U-shaped wire and a light slider supports a weight of 1.5×10−2N (see figure). The length of the slider is 30cm and its weight negligible. The surface tension of the liquid film is
 A(a) 0.0125Nm−1B(b) 0.1Nm−1C(c) 0.05Nm−1D(d) 0.025Nm−1
A(a) 0.0125Nm−1B(b) 0.1Nm−1C(c) 0.05Nm−1D(d) 0.025Nm−1A thin and light thread of sufficient length L is attached to a wire frame. The frame (along with the thread) is dipped into soap solution. When the frame is taken out of the solution, the thread takes the form of a semicircle with a soap film extending between the frame and the thread as shown in the figure (a). Now the thread is deformed into two semicircles by applying a force of F at the middle of the thread, as a result the film gets strectched as shown in the figure. (b). Calculate the surface tension of the soap solution.
 AπF2LBπFLC2πFLD14πFL
AπF2LBπFLC2πFLD14πFLChoose the most appropriate option.
A U-shaped wire is dipped in a soap solution and removed. The thin soap film formed between the wire and light slider supports a weight of 1.5×102 N. The length of the slider is 30 cm. What is the surface tension of the film?A3×10−3Nm−1B2×10−5Nm−1C4×10−4Nm−1D2.5×10−2Nm−1
A U-shaped wire is dipped in a soap solution, and removed. A thin soap film formed between the wire and a light slider supports a weight of 1.5×10−2N (which includes the small weigh of the slider). The length of the slider is 30cm. What is the surface tension of the film?
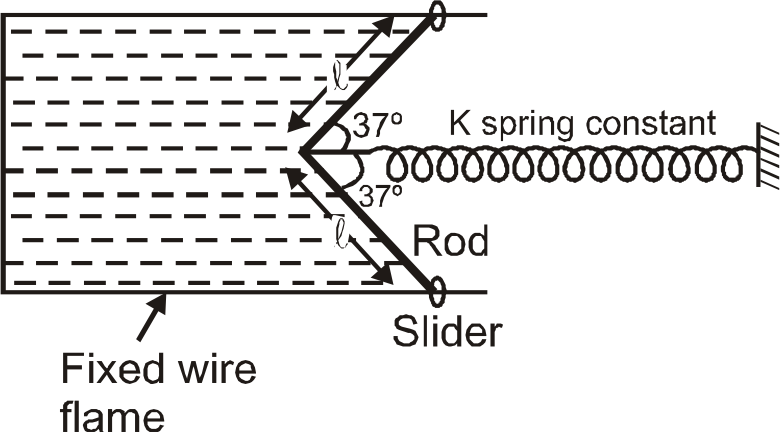
View SolutionA rigid bent light rod of total length 2l can slide on fixed wire frame with the help of frictionless sliders. There is thin liquid film (surface tension T) between bent rod and wire frame. In equilibrium the elongation in spring is given by (4Tlα5K). then find the value of α.
View SolutionA wire is bent in the form of a U-shape and a slider of negligible mass is connecting the two vertical sides of the U-shape. This arrangement is dipped in a soap solution and lifted a thin soap film is formed in t he frame it supports a wegith of 2.0×10−2 if the length of the slider is 40 cm whta is the surface tension of the film?
View SolutionA thin wire is bent in the form of a ring of diameter 3.0 cm . The ring is placed horizontally on the surface of soap solution and then raised up slowly . How much upward force is necessary to break the vertical film formed between the ring and the solution ? surface tension of a soap solution =3.0×10−2Nm−1.
View SolutionA thin liquid film formed between a U−shaped wire and a light slider supports a weight of 1.5×10−2N(see figure). The length of the slider is 30cm and its weight neligible. The surfaces tension of the liquid film is :

View Solution

