
A wire is bent an an angle θ. A rod of mass m can slide along the bended wire without friction as shown in Fig. A soap film is maintained in the frame kept in a vertical position and the rod is in equilibrium as shown in the figure. If rod is displaced slightly in vertical direction, then the time period of small oscillation of the rod is
2π√lg
2π√lcosθg
2π√lgcosθ
2π√lgtanθ
The correct Answer is:A
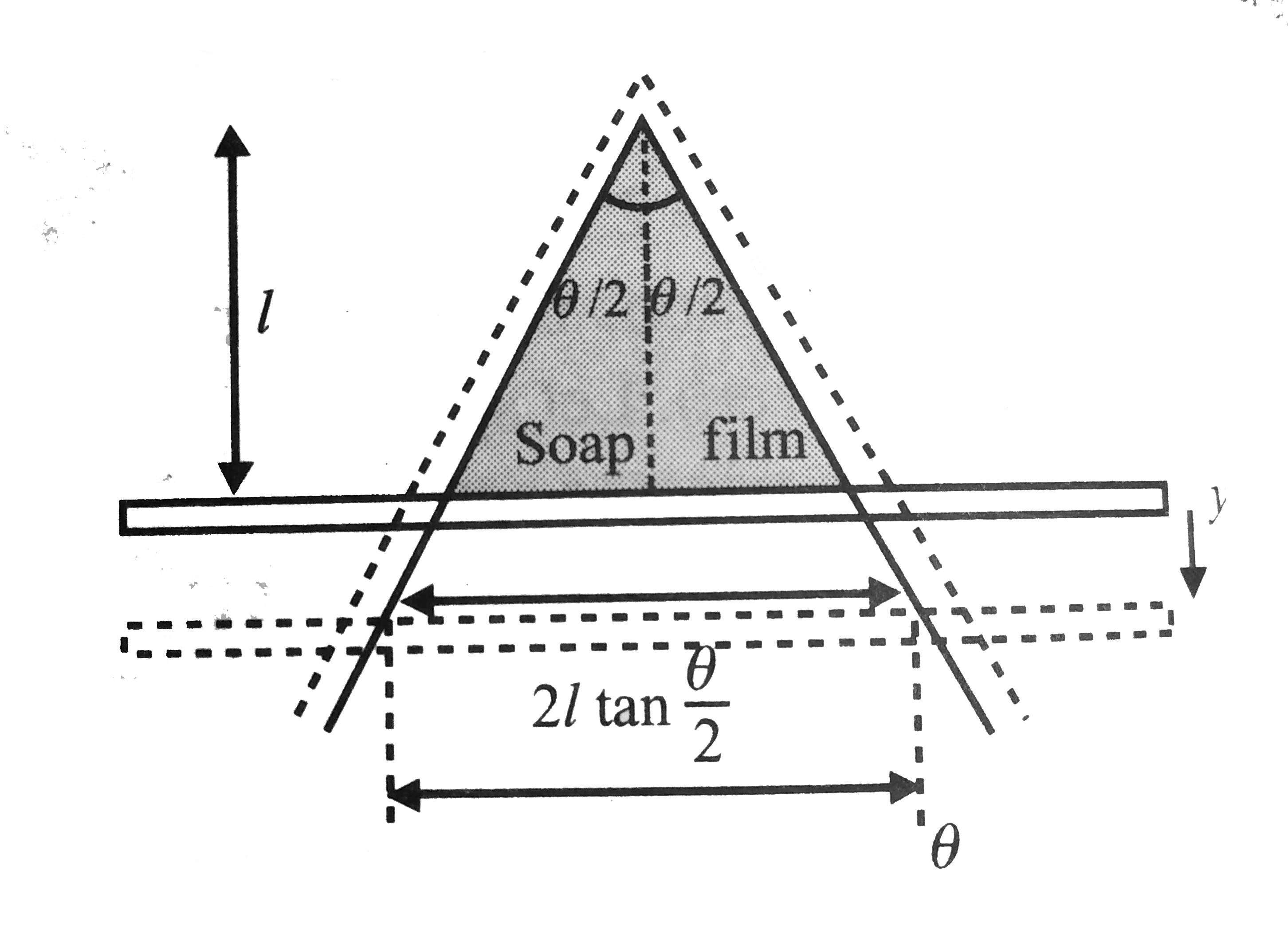
Let S be the surface tension of the soap film. For equilibrium of rod
2(l+y)tan(θ2)
mg=(Fsurface)1
mg=(2ltan(θ2)S×2, mg=4Sltan(θ2)
If the rod is displaced from its mean position by small displacement y, then restoring fornce on the rod is
Frest=−[(Fsurface)2−mg]−(Fsurface)1
=−[4S(l+y)tan(θ2)−mg]−[4Stan(θ2)y]
a=−4Stan(θ2)my=−4Stan(θ2)(4Sltan(θ2))
d2ydt2=−(gl)y ∵ T=2π√lg
Topper's Solved these Questions
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBook:CENGAGE PHYSICSChapter:LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONExercise:Multiple Correct
Explore 35 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBook:CENGAGE PHYSICSChapter:LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONExercise:Assertion Reasoning
Explore 6 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBook:CENGAGE PHYSICSChapter:LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONExercise:Subjective
Explore 21 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBook:CENGAGE PHYSICSChapter:KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSExercise:Interger
Explore 11 Videos
- MISCELLANEOUS KINEMATICSBook:CENGAGE PHYSICSChapter:MISCELLANEOUS KINEMATICSExercise:Interger type
Explore 3 Videos
Similar Questions
A rod of mass m can move vertically on two fixed inclined rod in vertical plane, weight of the rod is blanced by thin liquid film between rods as shown. (Surface tension of liquid is S).
If rod is displaced a little in downward direction and released, then what will be the time period of oscillation of rod.

View SolutionA small block is connected to a mass less rod, which is turn is attached to a spring of force constant k as shown in Fig. The blcok is displaced down slightly, and left free. Find time period of small oscillations.
View Solution
Knowledge Check
A unifrom rod of mass m and length l0 is pivoted at one end and is hanging in the vertical at one end and is hagingh in the vertical direction.The period of small angular oscillations of the rod is
 AT=3π√2l03gBT=4π√l03gCT=4π√2l03gDT=2π√2l03g
AT=3π√2l03gBT=4π√l03gCT=4π√2l03gDT=2π√2l03gA wire frame ABCD has a soap film. The wire BC can slide on the frame without friction and it is in equilibrium in the position shown in the figure. Find m, if T is the surface tension of the liquid.
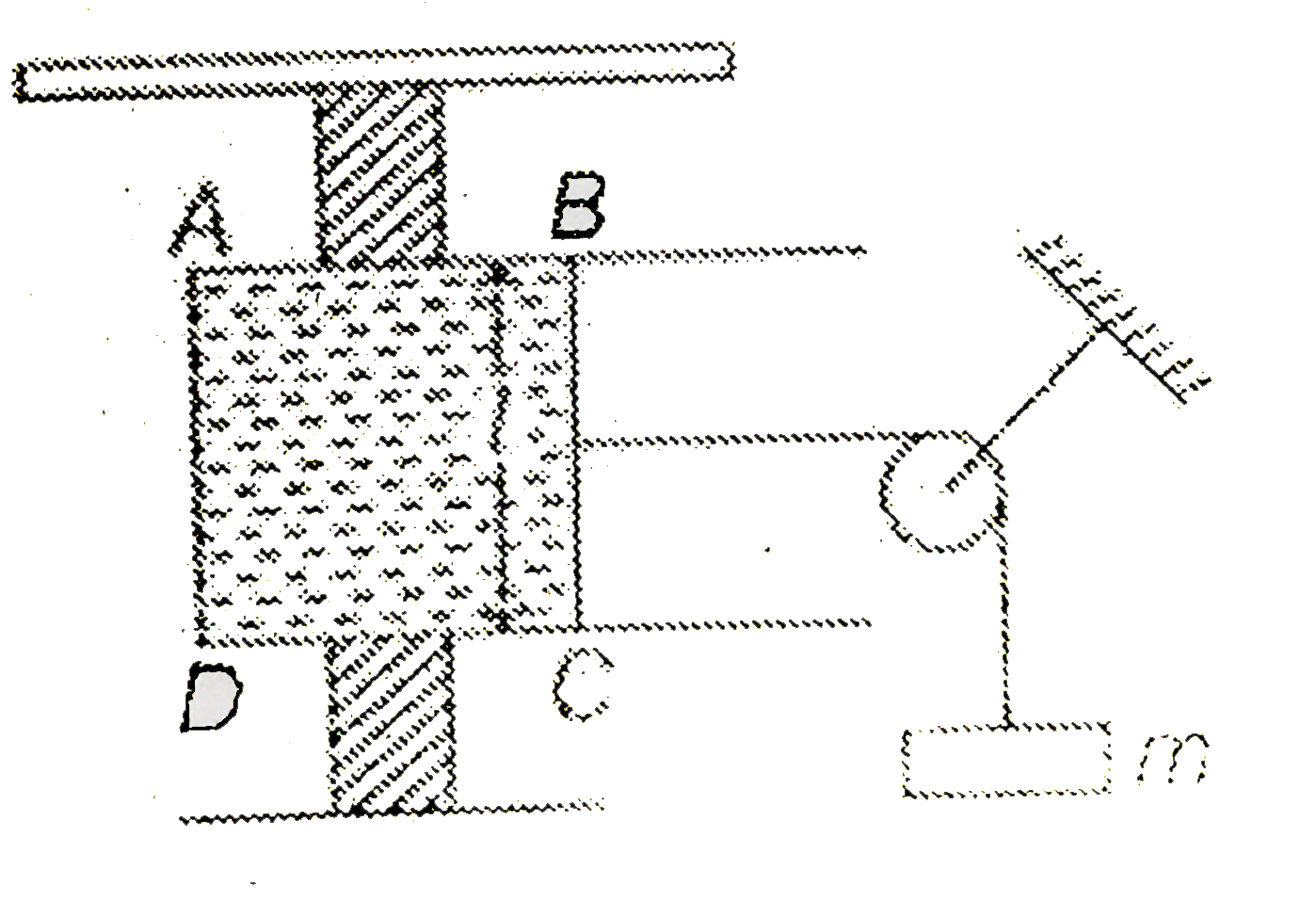 A2TlgBTlgCTl22gDTl2g
A2TlgBTlgCTl22gDTl2gA rod of mass m and length L is kept on a horizontal smooth surface. The rod is hinged at its one end A. There are two springs, perpendicular to the rod, kept in the same horizontal plane. The spring of spring constant k is rigidly attached to the lower end of rod and spring of spring constant 12k just touches the rod at its midpoint C, as shown in the figure. If the rod is slightly displaced leftward and released then, the time period for small osciallation of the rod will be
 Aπ√m3kB3π2√m3kCπ[√m3k+√3g2L]D3π2[√m3k+4√3g2L]
Aπ√m3kB3π2√m3kCπ[√m3k+√3g2L]D3π2[√m3k+4√3g2L]
A uniform rod ofmass M and length L is hanging from its one end free to rotate in a veritcal plane.A small ball of equal mass is attached of the lowe end as shown. Time period of small oscillations of the rod is

View SolutionA uniform nonconducting rod of mass ma and length l, with charge density λ as shown in fig. is hanged at the midpoint at orgin so that it can rotate in a horizontal plane without any friction. A uniform electric field E exists paralled to xaxis in th entire region. Calculated the period of small oscillation of the rod .

View SolutionA system of two identical rods (L-shaped) of mass m and length l are resting on a peg P as shown in the figure. If the system is displaced in its plane by a small angle θ,find the period of oscillations:

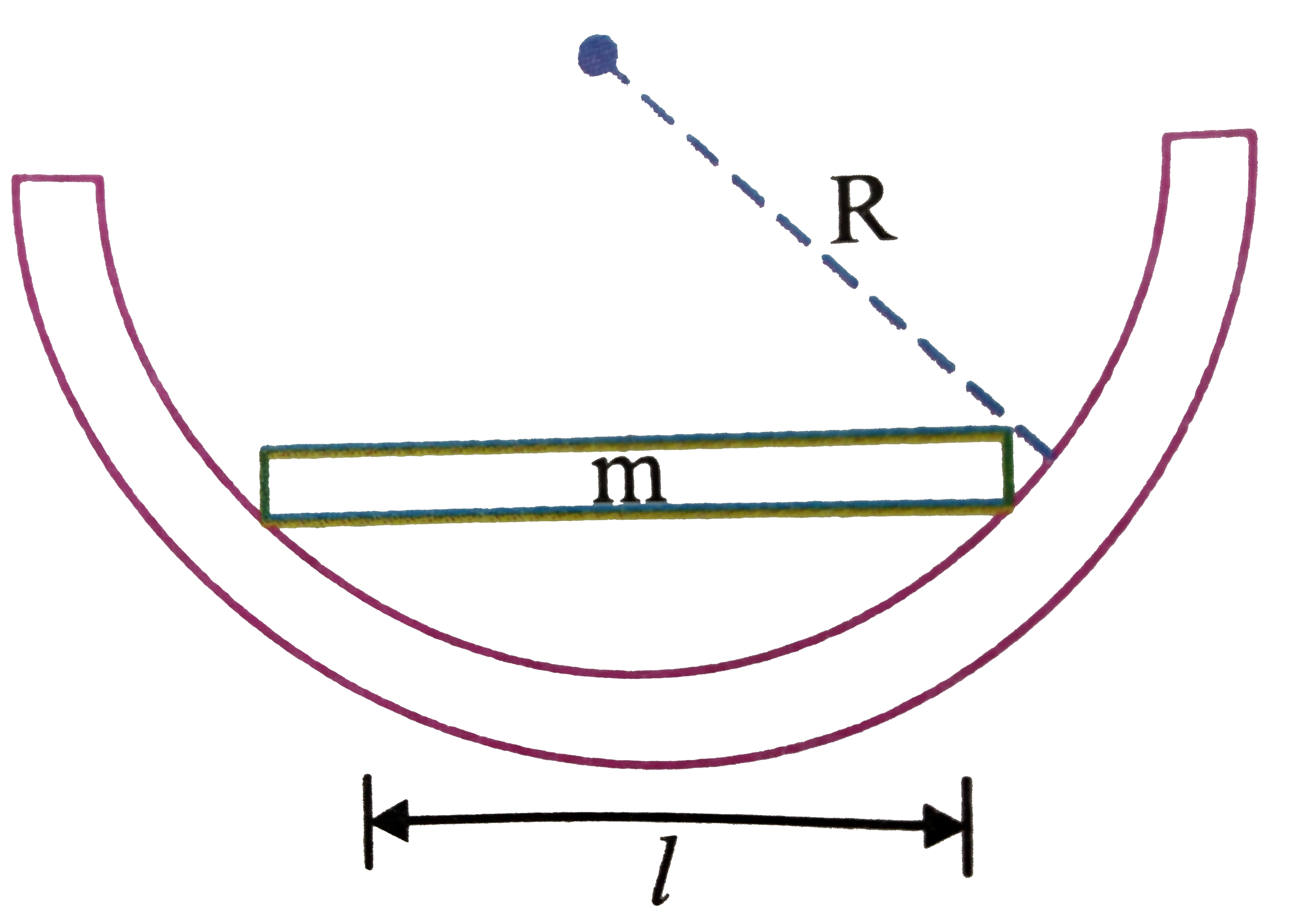
View SolutionA uniform rod of mass, m, and length l remains in equilibrium inside a smooth hemisphere of radius R as shown. The period of small oscillations of the rod is….. [∵r2=R2−l2/4]
View SolutionA small block is connected to a massless rod, which in turns attached to a spring of force constnat (K=2N/m) as shown in the fig. The block is displaced down slightly and left free. Find its time period.
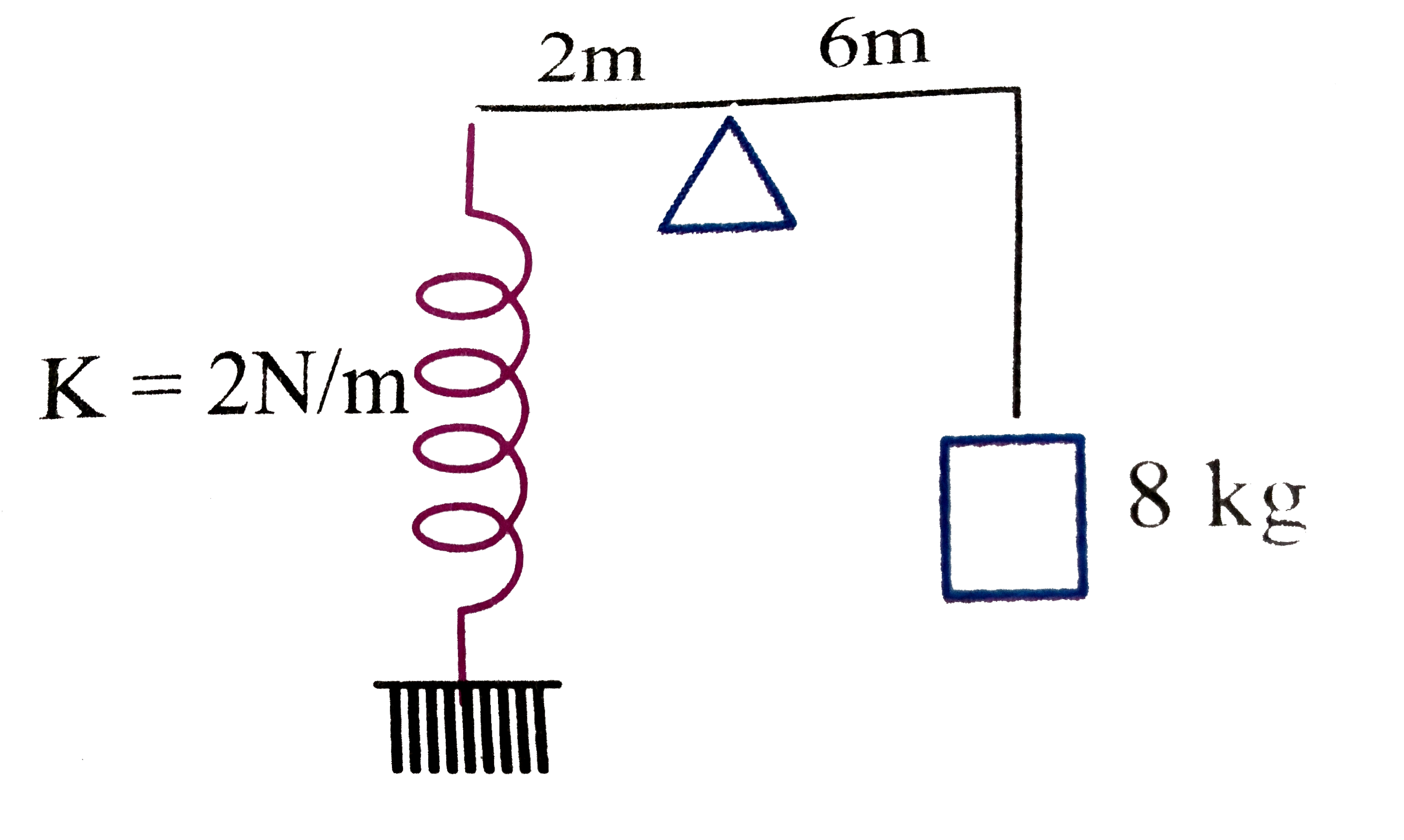
View Solution

