A small block is connected to a mass less rod, which is turn is attached to a spring of force constant k as shown in Fig. The blcok is displaced down slightly, and left free. Find time period of small oscillations.
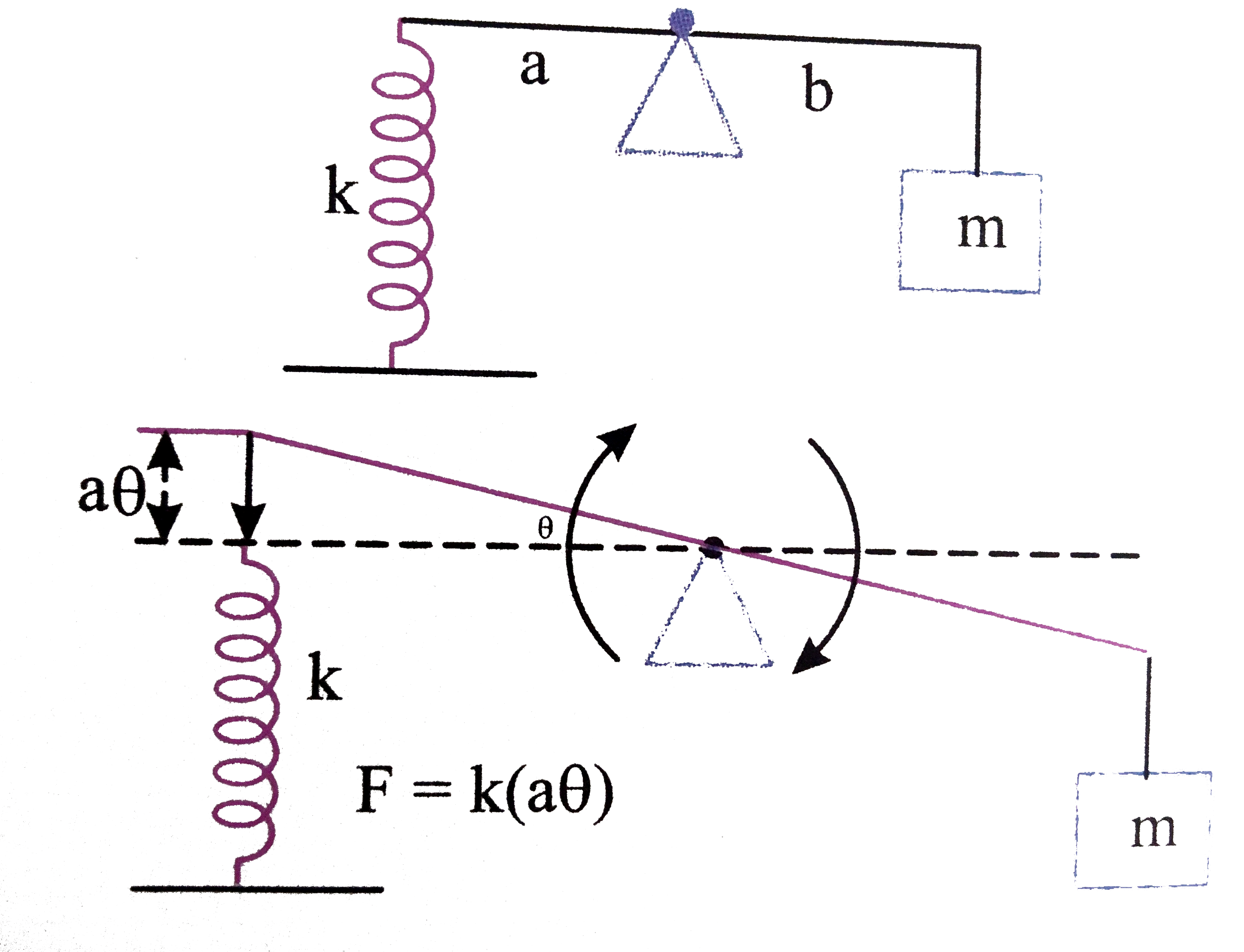
Let angular displacement of the block is θ, then extension of the spring will be 'a theta'. If F is the force in spring, then restoring torque, τrest=−Fa=−K(aθ)×a
[∵F=Kx=Kaθ] and =τrestI=Ka2I(−θ)
Now comparing with α=−ω2θ, we get
ω=√Ka2I and T=2π√IKa2
Here I=mb2∴T=2π√mb2Ka2=2πba√mK
Topper's Solved these Questions
- OSCILLATIONSBOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - C.U.Q
78 Videos
- OSCILLATIONSBOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - LEVEL -I (C.W)
34 Videos
- NEWTONS LAWS OF MOTIONBOOK - NARAYNACHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - PASSAGE TYPE QUESTION
6 Videos
- PHYSICAL WORLDBOOK - NARAYNACHAPTER - PHYSICAL WORLDEXERCISE - C.U.Q
10 Videos
Similar Questions
A block of mass m is connected to three springs as shown in Fig. The block is displaced down slightly and left free, it starts oscillating. Find time period of oscillations.
View SolutionA particle of mass m is attached with three springs A,B and C of equal force constancts k as shown in figure. The particle is pushed slightly against the spring C and released. Find the time period of oscillation.
 .
.
View Solution
Knowledge Check
A small block is connected to a massless rod, which in turns attached to a spring of force constnat (K=2N/m) as shown in the fig. The block is displaced down slightly and left free. Find its time period.
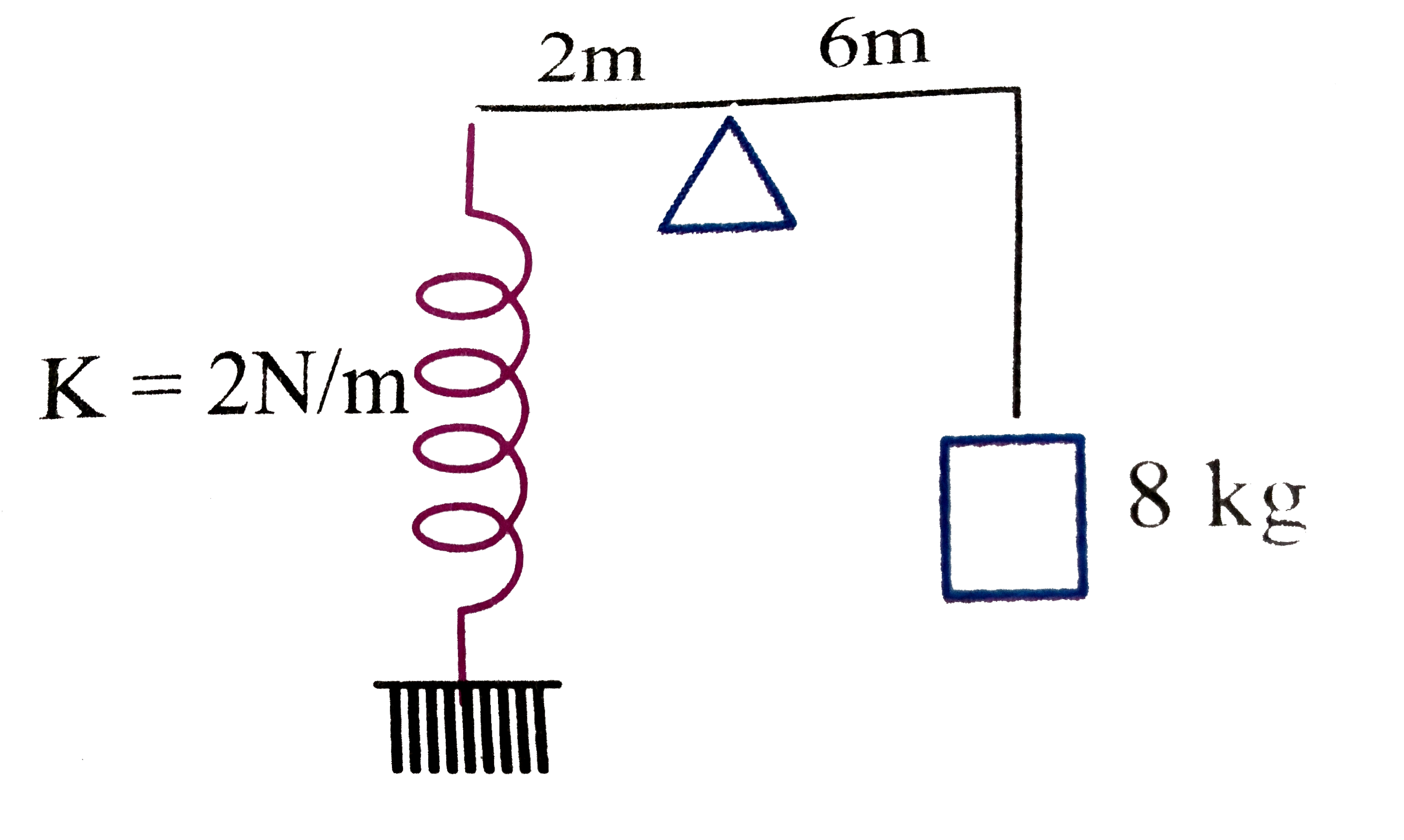 AπsecB2πsecC6πsecD12πsec
AπsecB2πsecC6πsecD12πsecA uniform disc of mass m is attached to a spring of spring constant k as shown in figure and there is sufficient friction to prevent slipping of disc. Time period of small oscillations of disc is:
 A2π√mkB2π√2m3kCπ√3m2kDπ√2m3k
A2π√mkB2π√2m3kCπ√3m2kDπ√2m3kA mass m is suspended from a spring of force constant k and just touches another idential spring fixed to the floras shown in the figure. The time period of small oscillation is
 A2π√mkBπ√mk+π√mk/2Cπ√m3k/2Dπ√mk+π√m2k
A2π√mkBπ√mk+π√mk/2Cπ√m3k/2Dπ√mk+π√m2k
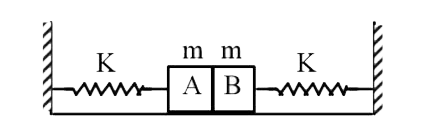
Two blocks each of mass m are connected with springs each of force constant K as shown in fig. The mass A is displaced to the left & B to the right by the same amount and released then the time period of oscillation is -
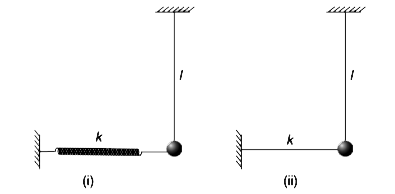
View SolutionA simple pendulum of length L has a bob of mass m. The bob is connected to light horizontal spring of force constant k. The spring is relaxed when the pendulum is vertical (see fig (i)).
(a) The bob is pulled slightly and released. Find the time period of small oscillations. Assume that the spring remains horizontal.
(b) The spring is replaced with an elastic cord of force constant k. The cord is relaxed when the pendulum is vertical (see fig (ii)). The bob is pulled slightly and released. Find the time period of oscillations.
View SolutionA block of mass m is connected with two ideal pullies and a massless spring of spring constant K as shown in figure. The block is slightly displaced from its equilibrium position. If the time period of oscillation is μπ√mK. Then find the value of μ.

View SolutionA block of mass m is connected to three springs as shown in the figure. The block is displaced down slightly and left free, it starts oscillating. Find the time period of oscillations (neglecting gravity). (m−π2(~kg):π2m10,θ−60∘,k1=4N / m , ki=23Nm)
'(##CEN_KSR_PHY_JEE_C16_E01_025_Q10##)'
View Solution
A mass m is suspended from a spring of force constant k and just touches another identical spring fixed to the floor as shown in the fig. The time period of small oscillations is
View Solution