The displacement x of a particle in motion is given in terms of time by x(x−4)=1−5cosωt
the particle executes SHM
the particle executes oscillatory motion which is not SHM
the motion of the particle is neither oscillatory nor simple harmonic
the particle is not acted upon by a force when it is at x = 4
The correct Answer is:A
x2−4x=1−5cosωt
x2−4x+4=5−5cosωt
(x−2)2=10 sin2ωt2
x−2=√10sinωt2
it is an SHM with A=√10 and angular frequency ω2
Topper's Solved these Questions
Similar Questions
The displacement x (in metre ) of a particle in, simple harmonic motion is related to time t ( in second ) as
x=0.01cos(πt+π4)
the frequency of the motion will be
View SolutionThe particle is moving such that its displacement along x-axis as a function of time is given by x(x−6)=1−10cosωt. Find amplitude, time period and mean position.
View Solution
Knowledge Check
The displacement x of a particle in a straight line motion is given by x=1−t−t2. The correct representation of the motion is
A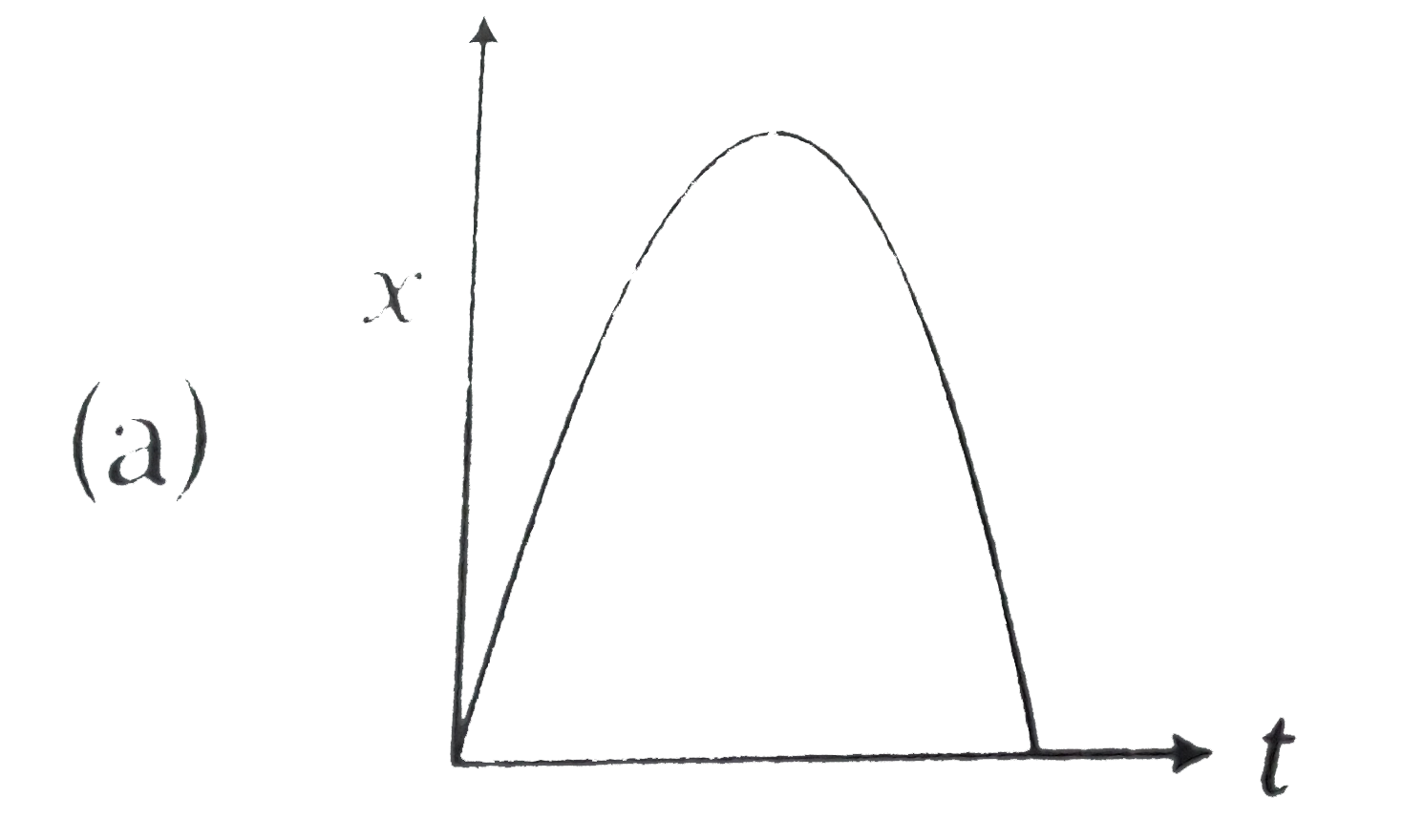 B
B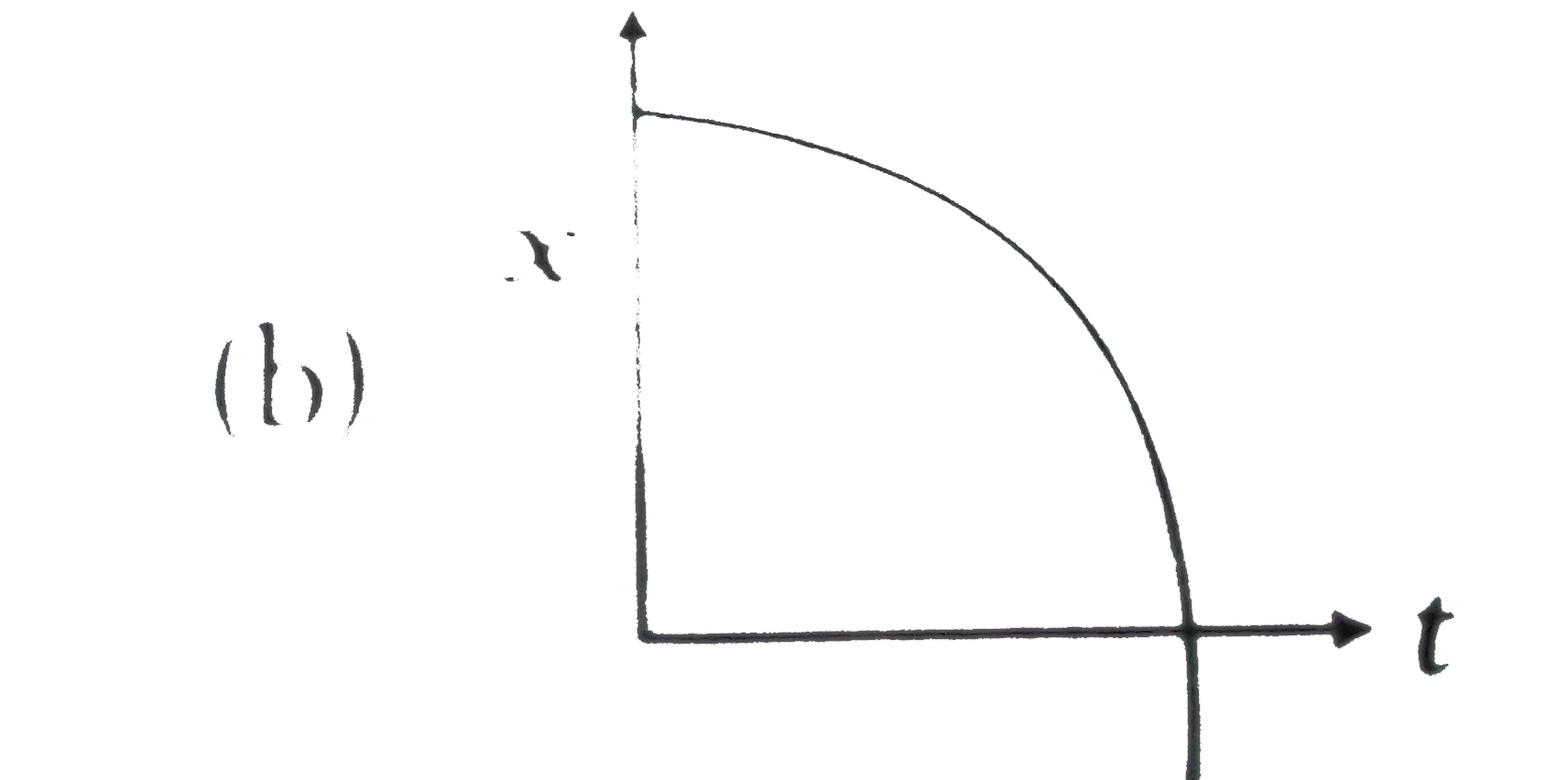 C
C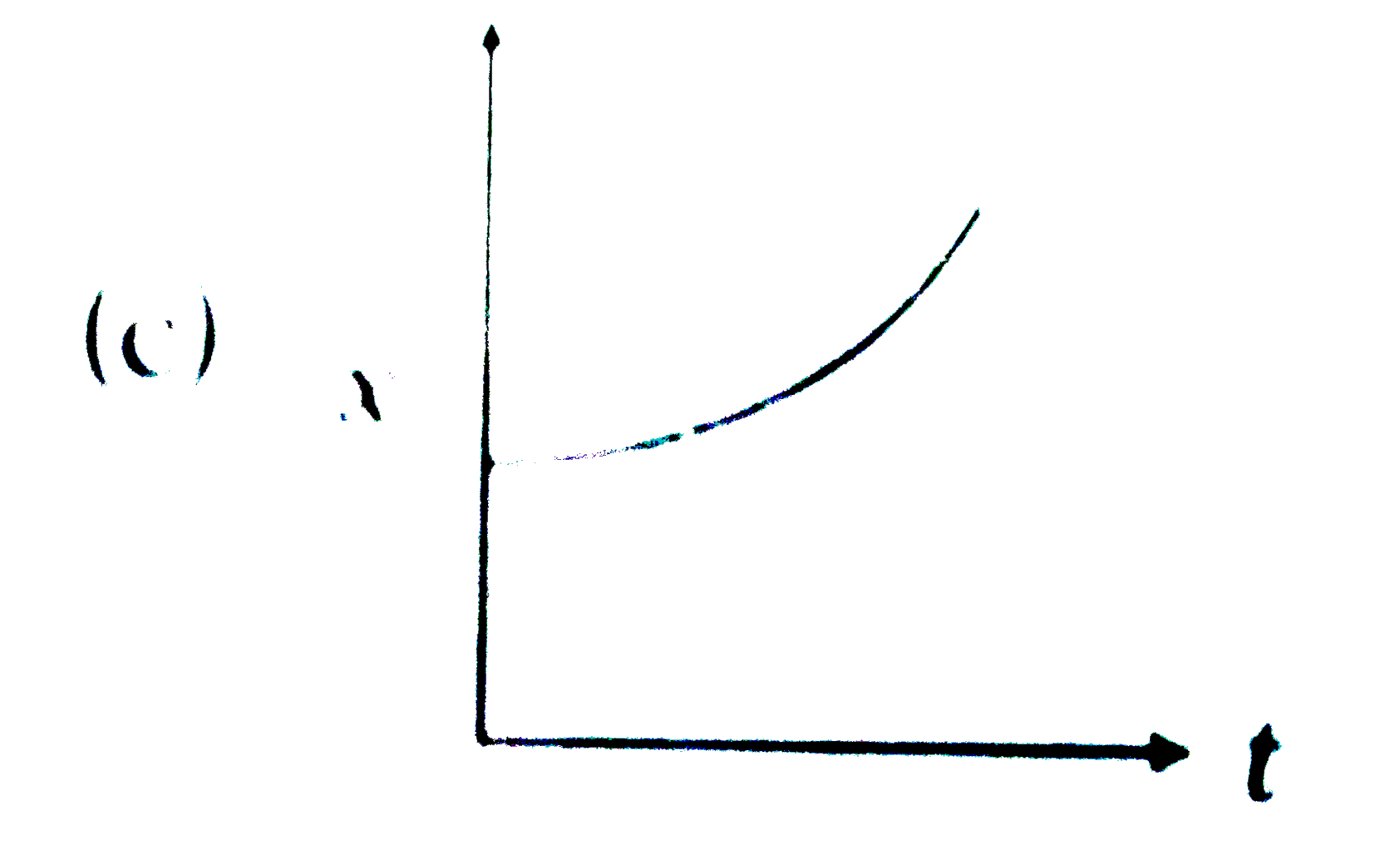 D
D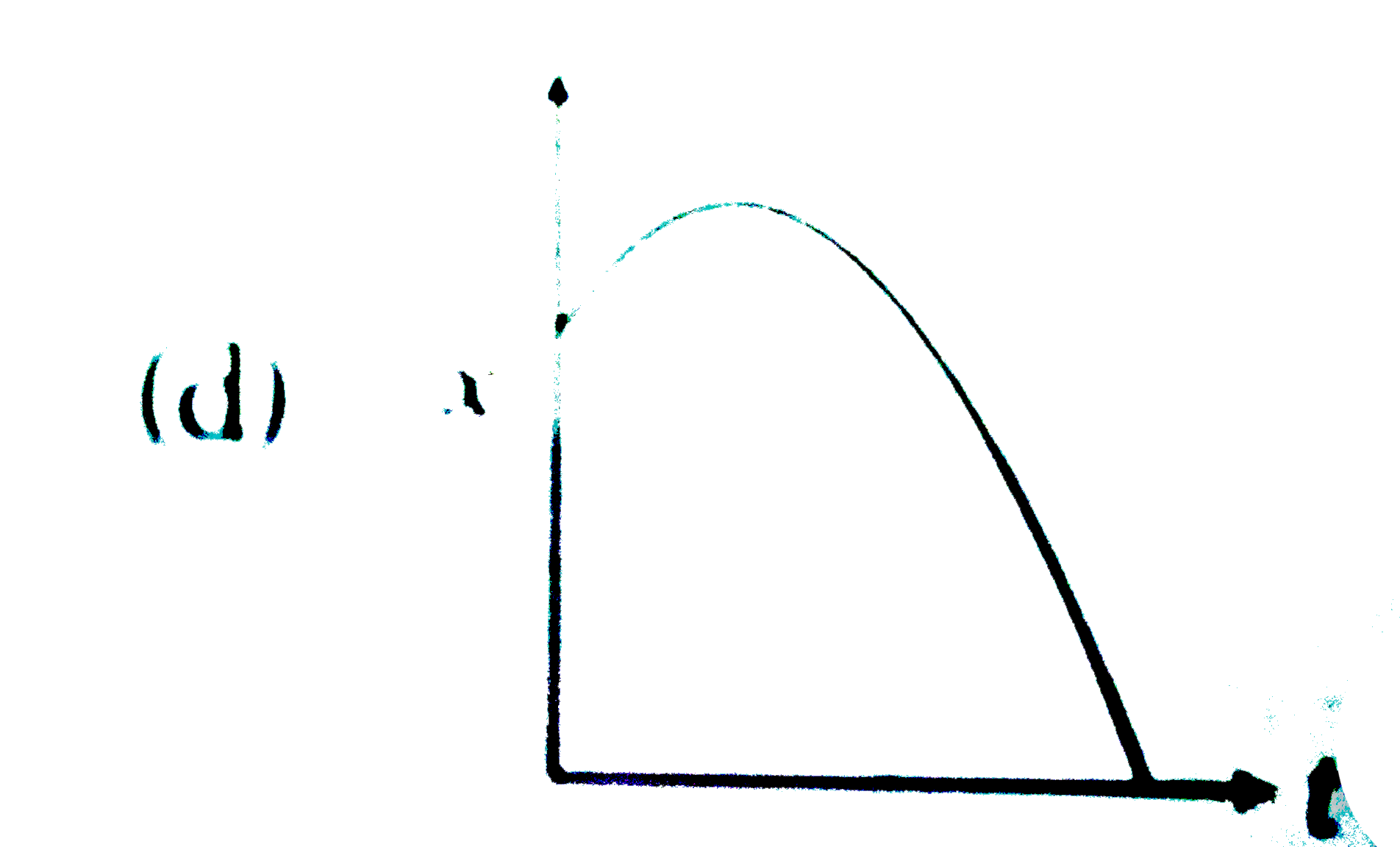
The displacement of a particle executing simple harmonic motion is given by y=A0+Asinωt+Bcosωt. Then the amplitude of its oscillation is given by
AA+BBA0+√A2+B2C√A2+B2D√A20+(A+B)2The displacemeent of a particle is given at time t by x=Asin(−2ωt)+Bsin2ωt. Then,
Athe motion of the particle is SHM with an amplitude of √A2+B24Bthe motion of the particle is not SHM, but oscillatory with a time period of T=πω.Cthe motion of the particle is oscillatory with a time period of T=π2ω.Dthe motion of the particle is a not periodic
The displacement of a particle performing simple harmonic motion is given by, x=8 sin ωt+6cos ωt, where distance is in cm and time is in second. What is the amplitude of motion?
View SolutionThe displacement s of a particle at time t is given by s=αsinωt+βcosωt then acceleration at time t is
View SolutionThe displacement of a particle executing a S.H.M. is given by x= A "sin" ωt+Acosωt. What is the amplitude of motion ?
View SolutionThe displacement of a particle is given by x=cos2ωt. The motion is
View SolutionThe instantaneous displacement x of a particle executing simple harmonic motion is given by x=a1sinωt+a2cos(ωt+π6). The amplitude A of oscillation is given by
View Solution

