The instantaneous displacement x of a particle executing simple harmonic motion is given by x=a1sinωt+a2cos(ωt+π6). The amplitude A of oscillation is given by
A
√a21+a22+2a1a2cos(π6)
B
√a21+a22+2a1a2cos(π3)
C
√a21+a22−2a1a2cos(π6)
D
√a21+a22−2a1a2cos(π3)
Video Solution
Text Solution
The correct Answer is:D
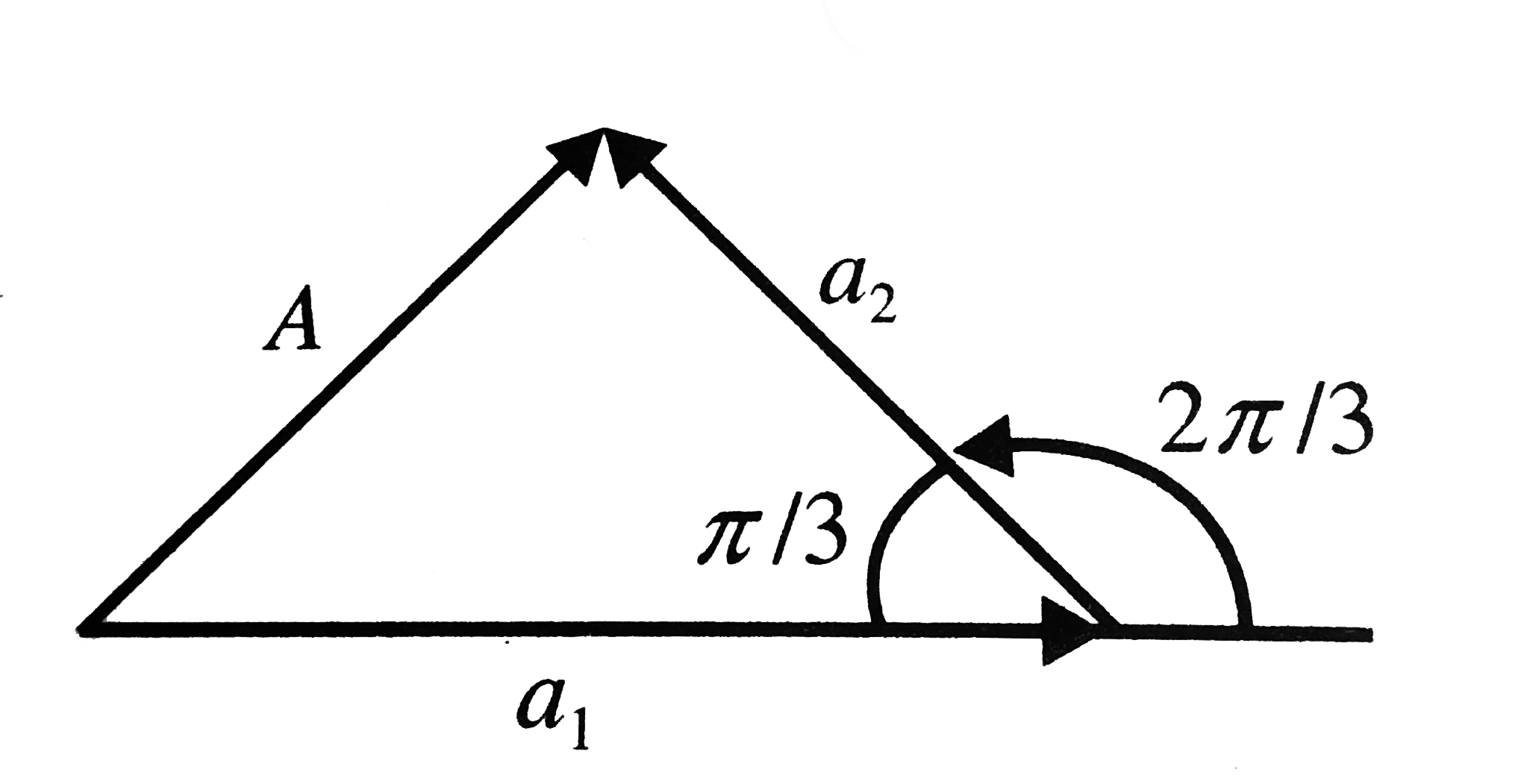
x=a1sinωt+a2cos(ωt+π6)
=a1sinωt+a2sin(ωt+π6+π2)
=a1sinωt+a2sin(ωt+2π3)
A2=a21+a22+2a1a2cos(2π3)
a21+a22−2a1a2cos(π3)
A=√a21+a22−2a1a2cos(π3)
|
Topper's Solved these Questions
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBook:CENGAGE PHYSICSChapter:LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONExercise:Multiple Correct
Explore 35 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBook:CENGAGE PHYSICSChapter:LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONExercise:Assertion Reasoning
Explore 6 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBook:CENGAGE PHYSICSChapter:LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONExercise:Subjective
Explore 21 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBook:CENGAGE PHYSICSChapter:KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSExercise:Interger
Explore 11 Videos
- MISCELLANEOUS KINEMATICSBook:CENGAGE PHYSICSChapter:MISCELLANEOUS KINEMATICSExercise:Interger type
Explore 3 Videos
Similar Questions
Knowledge Check
The displacement of a particle executing simple harmonic motion is given by y=A0+Asinωt+Bcosωt. Then the amplitude of its oscillation is given by
AA+BBA0+√A2+B2C√A2+B2D√A20+(A+B)2The displacement of a particle executing simple harmonic motion is given by
y=A0+Asinωt+Bcosωt
Then the amplitude of its oscillation is given by :AA0+√A2+B2B√A2+B2C√A20+(A+B)2DA+BThe phase of a particle executing simple harmonic motion is π2 when it has
AMaximum velocityBMaximum accelerationCMaximum energyDMaximum displacement
The displacement equation of a simple harmonic oscillator is given by y=Asinωt−Bcosωt
The amplitude of the oscillator will be
View SolutionThe amplitude of given simple harmonic motion is y=(3sinωt+4cosωt)m
View SolutionThe displacement of a particle executing a S.H.M. is given by x= A "sin" ωt+Acosωt. What is the amplitude of motion ?
View SolutionThe total energy of a particle having a displacement x, executing simple harmonic motion is
View SolutionThe displacement of a harmonic oscillator is given by x=αsinωt+βcosωt. Then the amplitude of the oscillator is,
View Solution

