A particle performs SHM about x=0 such that at t=0 it is at x=0 and moving towards positive extreme. The time taken by it to go from x=0 to x=A2 is time the time taken to go from x=A2 to a. The most suitable option for the blank space is
A
2
B
12
C
3AT
D
A2T
Video Solution
Text Solution
The correct Answer is:B
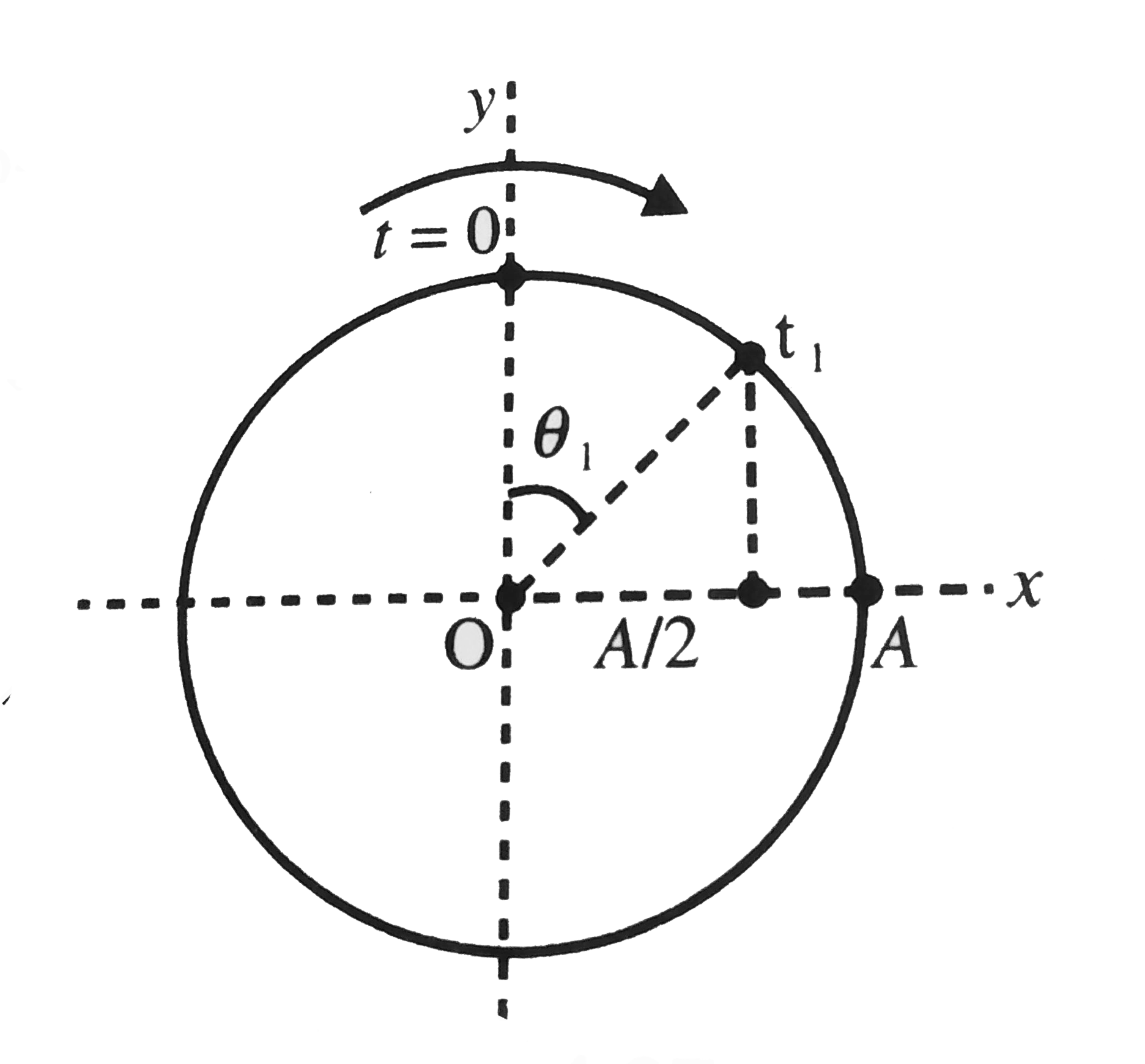
From circular motion representation we can represent SHM by uniform circular motion.
Let t1 is the time taken by paritcle to go from x=0 to x=A2
sinθ1=A2A=12
θ1=π6⇒ωt1=π6ω1=π×T6×2π=T12
So, time taken to go from x=A2 to A is
t2=T4−t1=T4−T12=T6
Hence t1t2=T12T6=12
|
Topper's Solved these Questions
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBook:CENGAGE PHYSICSChapter:LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONExercise:Multiple Correct
Explore 35 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBook:CENGAGE PHYSICSChapter:LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONExercise:Assertion Reasoning
Explore 6 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBook:CENGAGE PHYSICSChapter:LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONExercise:Subjective
Explore 21 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBook:CENGAGE PHYSICSChapter:KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSExercise:Interger
Explore 11 Videos
- MISCELLANEOUS KINEMATICSBook:CENGAGE PHYSICSChapter:MISCELLANEOUS KINEMATICSExercise:Interger type
Explore 3 Videos
Similar Questions
Knowledge Check
A particle executes simple harmonic motion between x=−Aandx=+A. The time taken for it to go from 0 to A/2. is T1 and to go from A/2 to A is T2. Then:
AT1<T2BT1>T2CT1=T2DT1=2T2A particle executes simple harmonic motion between x=−Aandx=+A. The time taken for it to go from 0→A/2isT1and→goomA/2→(A)is(T2). Then.
AT1<T2BT1>T2CT1=T2DT1=2T2A particle executes SHM in accordance with x=Asinωt. If t1 is the time taken by it to reach from x=0 to x=√3(A/2)and t2 is the time taken by it to reach from x=√3/2A to x=A , the value of t1/t2 is
A2B12C3DNone of the these
The time taken by a second pendulum to go from one extreme end to the other is ______
View SolutionA particle executes SHM of type x=asinω. It takes time t1 from x=0 to x=a2andt2 from x=a2 to x=a. The ratio of t1:t2 will be
View SolutionA particle executes SHM of type x=Asinωt. It takes time t1 from x=0 to x=A2andt2 from x=A2 to x=A. The ratio t1:t2 will be
View SolutionA particle performs SHM on x- axis with amplitude A and time period T .The time taken by the particle to travel a distance A/5 starting from rest is
View SolutionA particle exectes S.H.M. along a straight line with mean position x=0, period 20s amplitude 5cm. The shortest time taken by the particle to go form x=4cm to x=−3cm is
View Solution

