The acceleration of a particle moving along x-axis is a=−100x+50. It is released from x=2. Here a and x are in S.I units. The motion of particle will be:
periodic, oscillatory but not SHM.
periodic but not oscillatory
oscillatory but not periodic.
simple harmonic.
The correct Answer is:D
To solve the problem, we need to analyze the given acceleration equation and determine the nature of the motion of the particle.
1. Identify the given acceleration equation:
The acceleration of the particle is given by:
a=−100x+50
2. Rearrange the equation:
We can rearrange the equation to isolate the terms related to x:
a+100x=50
or
a=−100x+50
3. Identify the form of the equation:
The equation can be rewritten as:
a=−100x+50
This shows that the acceleration a is a linear function of displacement x.
4. Determine the nature of the motion:
In simple harmonic motion (SHM), the acceleration is directly proportional to the negative of the displacement from the equilibrium position. The general form for SHM is:
a=−kx
where k is a positive constant.
5. Analyze the constant term:
The presence of the constant term (+50) indicates that the system has a force acting on it that is not dependent on the displacement x. This means that the particle is not oscillating around the equilibrium position at x=0 but rather around a shifted equilibrium position.
6. Determine the equilibrium position:
To find the equilibrium position, we set the acceleration to zero:
0=−100x+50
Solving for x:
100x=50⟹x=0.5
This means the particle will oscillate around x=0.5.
7. Conclusion:
Since the acceleration is proportional to the negative of the displacement from the equilibrium position, the motion of the particle is indeed simple harmonic motion (SHM).
Final Answer:
The motion of the particle will be Simple Harmonic Motion (SHM).
The acceleration of the particle is given by:
a=−100x+50
We can rearrange the equation to isolate the terms related to x:
a+100x=50
or
a=−100x+50
The equation can be rewritten as:
a=−100x+50
This shows that the acceleration a is a linear function of displacement x.
In simple harmonic motion (SHM), the acceleration is directly proportional to the negative of the displacement from the equilibrium position. The general form for SHM is:
a=−kx
where k is a positive constant.
The presence of the constant term (+50) indicates that the system has a force acting on it that is not dependent on the displacement x. This means that the particle is not oscillating around the equilibrium position at x=0 but rather around a shifted equilibrium position.
To find the equilibrium position, we set the acceleration to zero:
0=−100x+50
Solving for x:
100x=50⟹x=0.5
This means the particle will oscillate around x=0.5.
Since the acceleration is proportional to the negative of the displacement from the equilibrium position, the motion of the particle is indeed simple harmonic motion (SHM).
The motion of the particle will be Simple Harmonic Motion (SHM).
Topper's Solved these Questions
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBook:CENGAGE PHYSICSChapter:LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONExercise:Multiple Correct
Explore 35 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBook:CENGAGE PHYSICSChapter:LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONExercise:Assertion Reasoning
Explore 6 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBook:CENGAGE PHYSICSChapter:LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONExercise:Subjective
Explore 21 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBook:CENGAGE PHYSICSChapter:KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSExercise:Interger
Explore 11 Videos
- MISCELLANEOUS KINEMATICSBook:CENGAGE PHYSICSChapter:MISCELLANEOUS KINEMATICSExercise:Interger type
Explore 3 Videos
Similar Questions
The acceleration of a particle moving along x -axis is a= −100x.It is released from rest at x=2.Here a and x are in S.I.units.The minimum time taken by particle to go from x=2 to x=0 is πα seconds.Find the value of α4.
View Solutionx-coordinate of a particle moving along this axis is x=(2+t2+2t3). Here, x is in meres and t in seconds. Find (a) position of particle from where it started its journey, (b) initial velocity of particle and (c) acceleration of particle at t=2s.
View Solution
Knowledge Check
The acceleration of a particle moving along x-axis is a = –200 x + 50. It is released from x = 2. Here 'a' and 'x' are in S.I. units. The motion of particle will be :-
APeriodic, oscillatory but not SHMBPeriodic but not oscillatoryCOscillatory but not periodicDSimple harmonicThe acceleration of a particle is a=−100x+50. It is released from x=2. Here, a and x are in SI units
Athe particle will perform SHM of amplitude 2mBthe particle will perform SHM of amplitude 1.5mCthe particle will perform SHM of time period 0.63sDthe particle will have a maximum velocity of 15m/sFor a particle moving along the x-axis, mark the correct statement(s).
Aif x is positive and is increasing with the time, then average velocity of the particle is positive.Bif x is negative and becoming positive after some time, then the velocity of the particle is always positive.CIf x is negative and becoming less negative as time passes, then the average velocity of the particle is positive.DIf x is positive and is increasing with time, then the velocity of the particle is always positive.
The position x of particle moving along x-axis varies with time t as x=Asin(ωt) where A and ω are positive constants. The acceleration a of particle varies with its position (x) as
View SolutionThe displacement of a particle moving along x-axis is given by :
x=a+bt+ct2
The acceleration of the particle is.
View SolutionThe velocity (υ) of a particle moving along X-axis varies with its position x as shown in figure. The acceleration (a) of particle varies with position (x) as
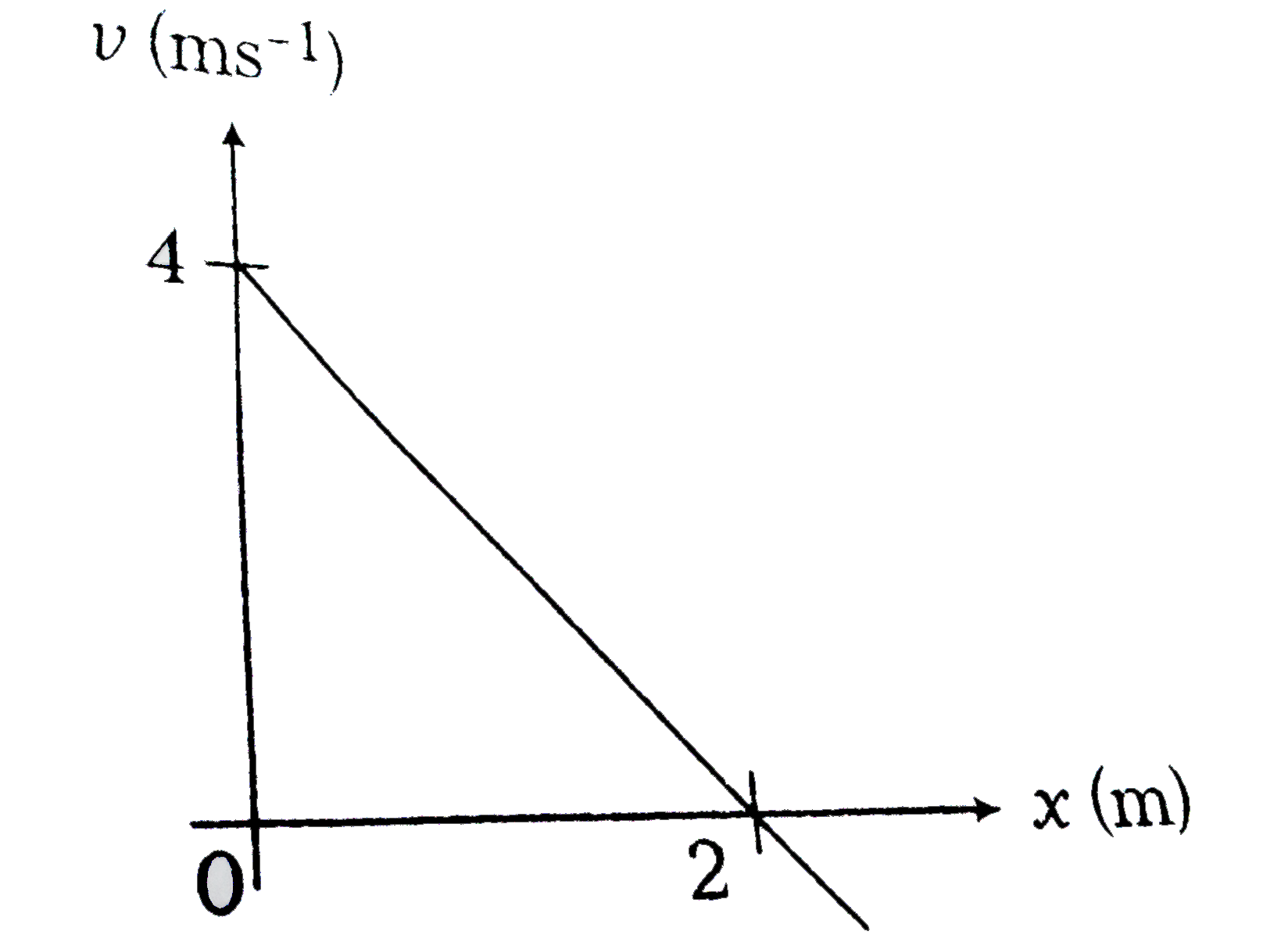
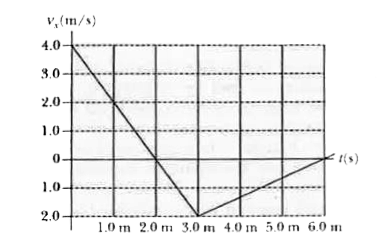
View Solutionvx is the velocity of a particle moving along the x-axis as shown in the figure. If x=2.0m at t=1.0s, what is the position of the particle at t=6.0s ?
View SolutionA particle constrained to move along x-axis given a velocity u along the positive x-axis. The acceleration ' a ' of the particle varies as a = - bx, where b is a positive constant and x is the x co-ordinate of the position of the particle . Then select the correct alternative(s): .
View Solution

