A point charge Q1=−125μC is fixed at the center of an insulated disc of mass 1 kg. The disc rests on a rough horizontal plane. Another charge Q2=125μC is fixed verically above the center of the disc at a height h=1m. After the disc is displaced slightly in the horizontall direction (friction is sufficient to prevent slipping), find the period of oscillation of disc.

The correct Answer is:2π(hQ)√(6πε0Mh).
Let the radius of the disc be R. If the disc is displaced x, The corresponding angular dispalcement θ=x/R.
The restoring torque τ about the point of contact of disc with ground.
τp=(Fsinθ)R
(Fsinθ)R=1α=[(MR)22+MR2]α
where F=Q2x4πε0(h2+x2)
and sinθ=R√(h2+x2)
Hence Q2xR4πε0(h2+x2)3/2=[MR22+MR2]α
or α=Q2x6πε0MR(h2+x2)3/2
for x<<h,α≅−Q2x6πε0MRh3
α=aR≅−Q2x6πε0MRh3
Negative sign is being introduced because angular acceleration and angular displacement are opposite to each other. Thus, ltbr> a=Q2x6πε0MRh3
Hence, ω=√Q26πε0MRh3
T=2π√6πε0MRh3Q2=2π(hQ)√(6πε0Mh).
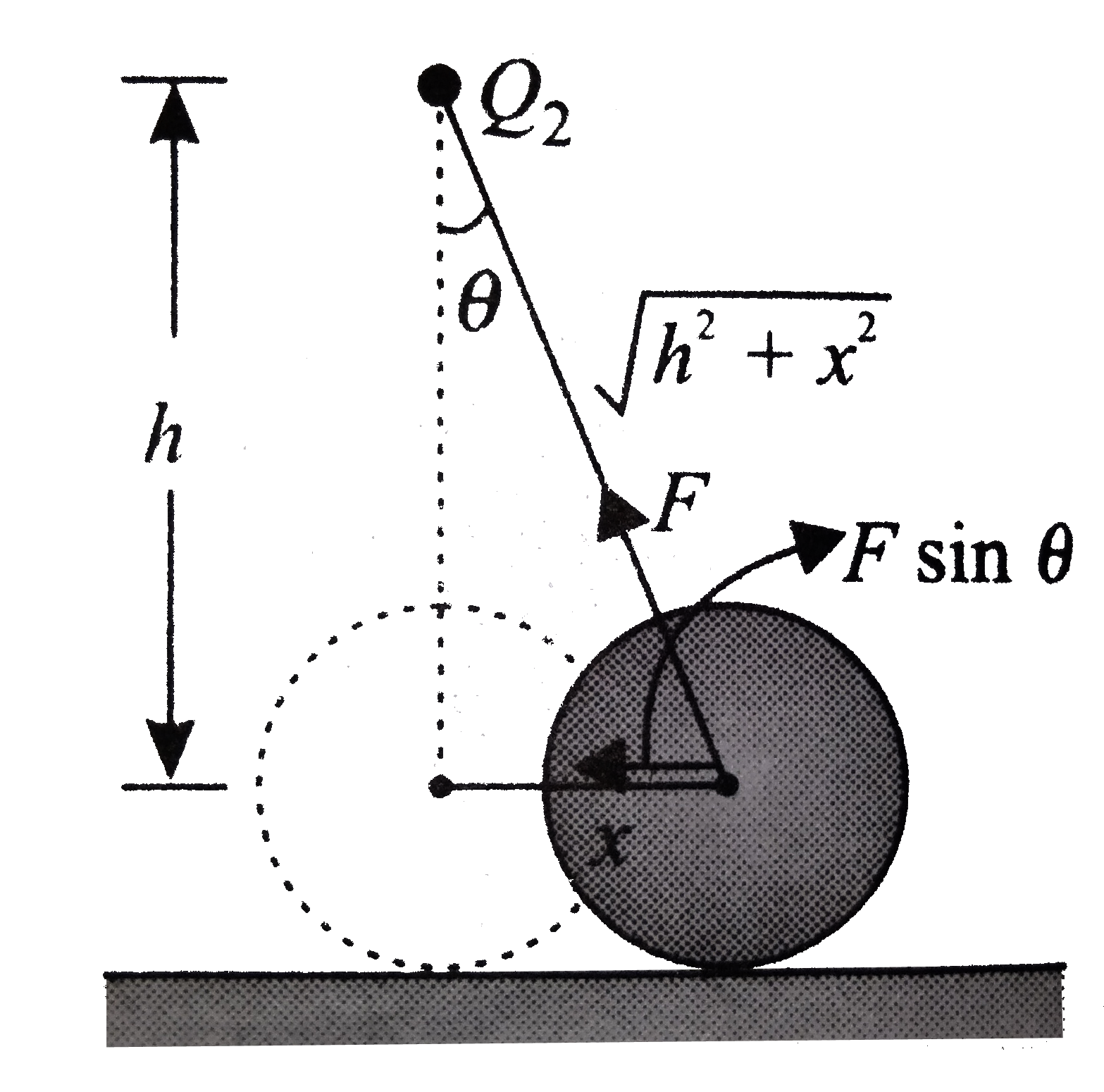
Topper's Solved these Questions
- COULOMB LAW AND ELECTRIC FIELDBook:CENGAGE PHYSICSChapter:COULOMB LAW AND ELECTRIC FIELDExercise:Single Correct
Explore 47 Videos
- COULOMB LAW AND ELECTRIC FIELDBook:CENGAGE PHYSICSChapter:COULOMB LAW AND ELECTRIC FIELDExercise:Multiple Correct
Explore 8 Videos
- COULOMB LAW AND ELECTRIC FIELDBook:CENGAGE PHYSICSChapter:COULOMB LAW AND ELECTRIC FIELDExercise:Exercises
Explore 58 Videos
- COMMUNICATION SYSTEMBook:CENGAGE PHYSICSChapter:COMMUNICATION SYSTEMExercise:QUESTION BANK
Explore 19 Videos
- Current ElectricityBook:CENGAGE PHYSICSChapter:Current ElectricityExercise:QUESTION BANK
Explore 40 Videos
Similar Questions
There is a disc of mass M and radius R. A pont charge +Q and of mass m is fixed at the centre of the disc. The disc is held on a fixed horizontal rough suface . Another point charged +q is fixed on the surface such that disance between +q and +Q is 4R3. Now the disc is set free. If the disc does not loose contact with the ground at the same intent the relation must hold is M>ηm. Find η. (Use 27Qq256πε0R2=3mg)

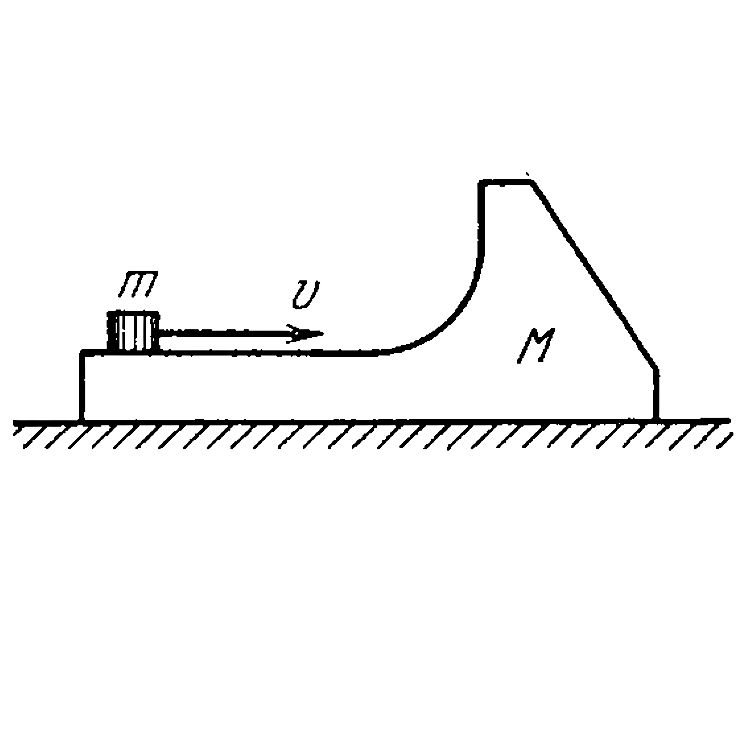
View SolutionA body of mass M (figure) with a small disc of mass m placed on it rests on a smooth horizontal plane. The disc is set in motion in the horizontal direction with velocity v. To what height (relative to the initial level) will the disc rise after breaking off the body M? The friction is assumed to be absent.
View Solution
Knowledge Check
Charge Q is uniformly distributed on the rim of a thin insulating disc of mass m which is initially at rest and placed on a smooth horizontal surface. What will be the angular velocity of the disc if a magnetic field B, perpendicular to the plane of the disc is switched on ?
 AQB/2mBQB/3mC2QB/3mDQB/m
AQB/2mBQB/3mC2QB/3mDQB/mA uniform solid disc of mass 1 kg and radius 1m is kept on a rough horizontal surface.

Two forces of magnitude 2N and 4N have been applied on the disc as shown in the figure. Linear acceleration of the center of mass of the disc is if there is no slipping isA4m/s2B2m/s2C1m/s2DzeroA disc having uniform surface charge density in upper part +ρ and −ρ in lower half placed on rough horizontal surface as shown in figure. A uniform electric field is set up as shown if mass of disc is M and its radius is R as well sufficient friction is present to prevent slipping. The acceleration of disc is
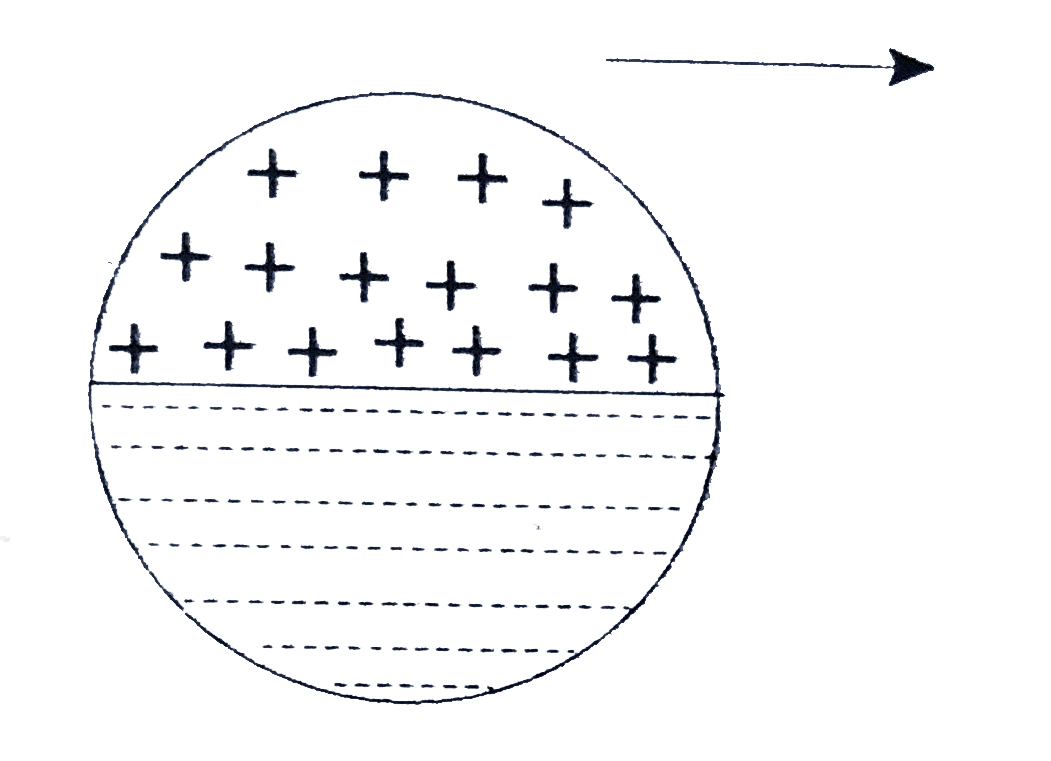 A89ρR2E0MB98ρR2E0MC43ρR2E0MD34ρR2E0M
A89ρR2E0MB98ρR2E0MC43ρR2E0MD34ρR2E0M
A heavy circular disc of mass M is revolving in a horizontal plane with angular speed ω0 about its center which is fixed. An insect of mass m walks from the center to the edge and then files away. Find the final angular speed of disc.
View SolutionFour point charges qA=2μC,qB=−5μC,qC=−2μCandqD=−5μC are located at the corners of a square ABCD of side 10 cm. What is the force on a charge of 1μC placed at the center of the square ?
View SolutionA disc shaped body (having a hole shown in the figure) of mass m=10kg and radius R=109m is performing pure rolling motion on a rough horizontal surface. In the figure point O is geometrical center of the disc and at this instant the centre of mass C of the disc is at same horizontal level with O. The radius of gyration of the disc about an axis pasing through C and perpendicular to the plane of the disc is R2 and at the insant shown the angular velocity of the disc is ω=√gR rad/sec in clockwise sence. g is gravitation acceleration =10m/s2. Find angular acceleation α ( in rad/s2) of the disc at this instant.

View SolutionA point charge q is located on the axis of a disc of radius R at a distance b from the plane of the disc as shown in figure 1.295 What should be the radius of the disc if one fourth of the total electric flux form the charge passes through the disc.

View SolutionA uniform circular disc of radius r . 1placed on a rough horizontal plane has initial velocity v0 and an angular velocity ω0 as shown. The disc comes to rest after moving some distance in the direction of motion. Then
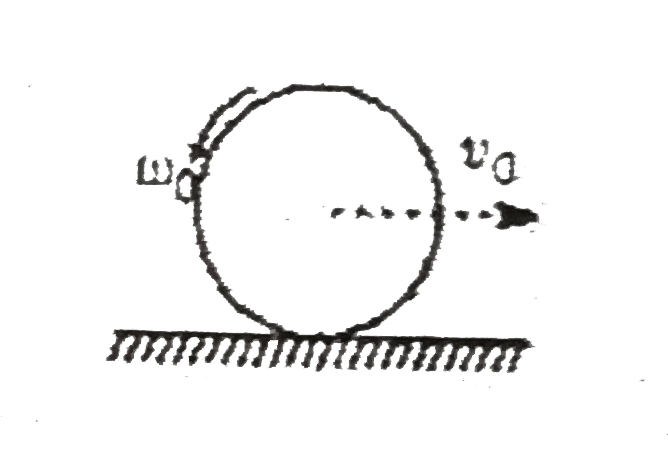
View Solution