A charged particle q of mass m is in wquilibrium at a height h from a horizontal infinite line charge wit uniform linear charge density λ. The charge lies in the vertical plane containing the line charge. If the particle is displaced slightly (vertically) prove that the motion of the charged particle will be simple harmonic. Also find its time period.
The correct Answer is:2π√mh22kqλ
At equilibrium mg=qE
mg=q2kλh

when particle is displaced to distance x in upwar direction. Then net force in upward direction is
F=q(2kλh+x)−mg
=2kqλh(1+xh)−1−mg=2kqλh(1+xh)−mg
=−(2kqλh2)x=−K0x
∴F∝−x (Motion is SHM)
Time period of motion is T=2π√mK0=2π√mh22kqλ.
Topper's Solved these Questions
- COULOMB LAW AND ELECTRIC FIELDBook:CENGAGE PHYSICSChapter:COULOMB LAW AND ELECTRIC FIELDExercise:Single Correct
Explore 47 Videos
- COULOMB LAW AND ELECTRIC FIELDBook:CENGAGE PHYSICSChapter:COULOMB LAW AND ELECTRIC FIELDExercise:Multiple Correct
Explore 8 Videos
- COULOMB LAW AND ELECTRIC FIELDBook:CENGAGE PHYSICSChapter:COULOMB LAW AND ELECTRIC FIELDExercise:Exercises
Explore 58 Videos
- COMMUNICATION SYSTEMBook:CENGAGE PHYSICSChapter:COMMUNICATION SYSTEMExercise:QUESTION BANK
Explore 19 Videos
- Current ElectricityBook:CENGAGE PHYSICSChapter:Current ElectricityExercise:QUESTION BANK
Explore 40 Videos
Similar Questions
Knowledge Check
Consider an infinite line charge having uniform linear charge density and passing through the axis of a cylinder is removed.
 AdecreaseBincreasesCremains sameDcannot say
AdecreaseBincreasesCremains sameDcannot sayFor an infinite line of charge having linear charge density λ lying along x-axis the work done in moving a charge q form C to A along CA is
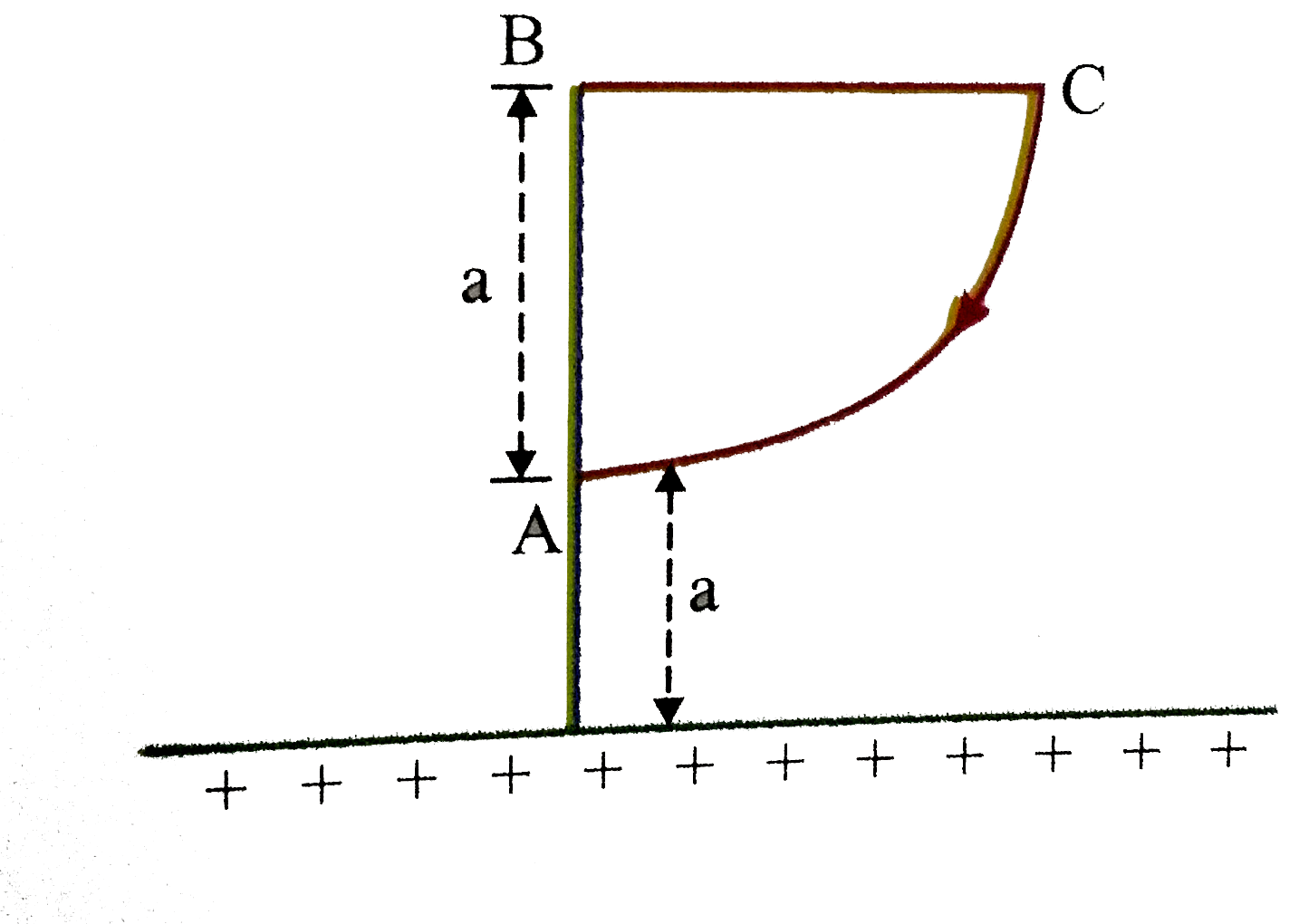 Aqλ2πε0In2Bqλ2πε0In√2Cqλ4πε0In2Dqλ2πε0In(0.5)
Aqλ2πε0In2Bqλ2πε0In√2Cqλ4πε0In2Dqλ2πε0In(0.5)A particle of charge −q and mass m moves in a circle of radius r around an infinitely long line charge of linear charge density +λ. Then, time period will be
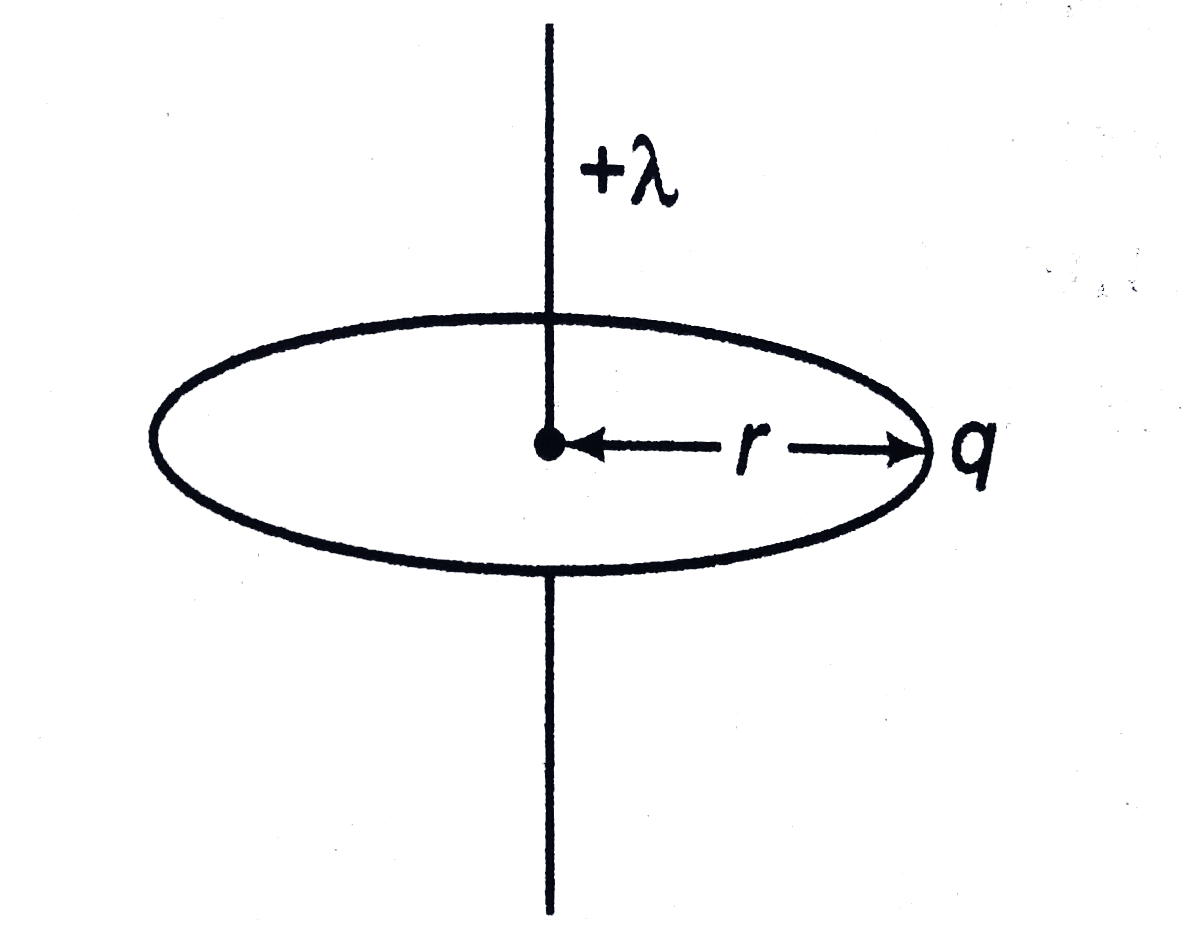 where , k=14πε0)AT=2πr√(m2kλqBT2=4π2m2kλqr3CT=12πr√2kλwmDT=12πr√m2kλq
where , k=14πε0)AT=2πr√(m2kλqBT2=4π2m2kλqr3CT=12πr√2kλwmDT=12πr√m2kλq
A charged particle of mass m having charge q remains in equilibrium at height d above a fixed charge Q. Now the charged particle is slightly displaced along the line joining the charges, show that it will executes S.H.M. and find the time period of oscillation.
View SolutionA particle of mass m and charge q is located midway between two fixed charged particles each having a charge q and a distance 2l apart. Prove that the motion of the particle will be SHM if it is displaced slightly along the line connecting them and released. Also find its time period.
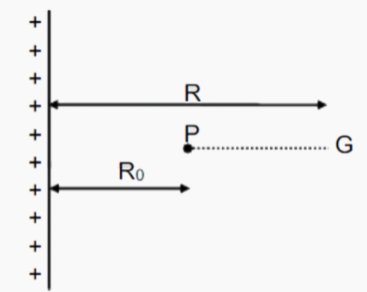
View SolutionA charge particle q is released at a distance R∘ from the infinite long wire of linear charge density λ. Then velocity will be proportional to (At distance R from the wire)
View SolutionA negatively charged particle is situated on a striaght line joining two other charge particle stationary of motion of the negatively charged particle will depend on
View SolutionConsider an infinite line charge having uniform linear charge density and passing through the axis of a cyclinder. What will be the effect on the flux passing through curved surface if the portions of the line charge outside the cyclinder is removed

View Solution


