A ball of radius R carries a positive charges whose volume density at a point is given as ρ=ρ0(1−r/R), Where ρ0 is a constant and r is the distance of the point from the center. Assume the permittivies of the ball and the enviroment to be equal to unity.
(a) Find the magnitude of the electric field strength as a function of hte distance r both inside and outside the ball.
(b) Find the maximum intensity Emax and the corresponding distance rm.
The correct Answer is:For r<R,E=kqr2=ρ0r3ε0[1−3r4R],
For r>R, E=(kq)/(r^(2))=(rho_(0)R^(3))/(12 epsilon_(0)r^(2))
Charge within radius r is
q=∫r0ρ0[1−rR]4πr2dr
=4πρ0∫r0(r2−r3R)dr
=4πρ0(r33−r44R)…(i)
For r<R
E=kqr2=ρ0r3ε0[1−3r4R] …(ii)
For total charge, put r=R in eq.(i)
Q=4πρ0[R33−R34]=4πρ0R312
For r>R,
E=kQr2=ρ0R312ε0r2...(iii)
At surface from both eqs, (ii) and (iii) put r=R,
E0=ρ0R12ε0
Also, at r=R/3
E=ρ0R12ε0.
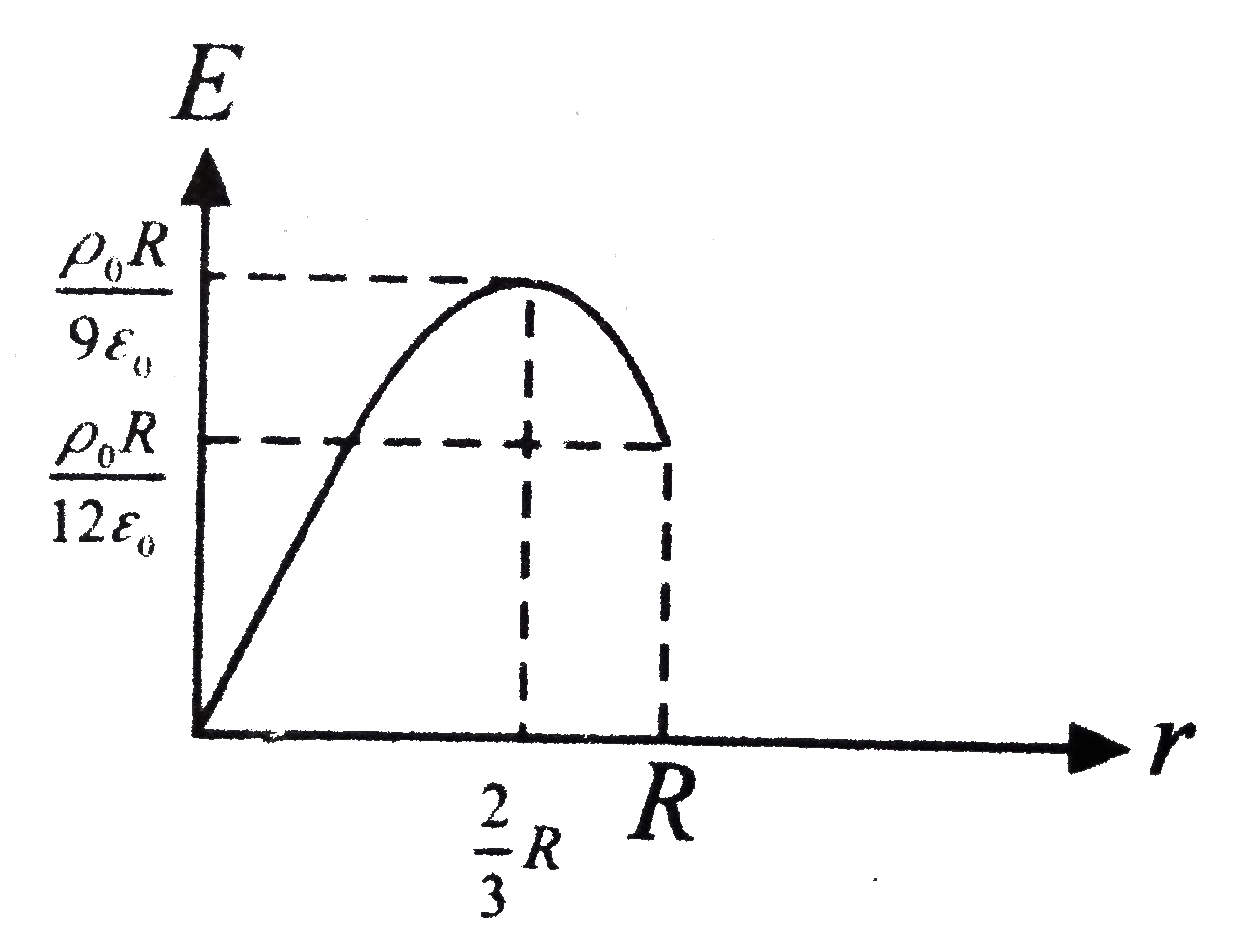 .
.
Topper's Solved these Questions
- COULOMB LAW AND ELECTRIC FIELDBook:CENGAGE PHYSICSChapter:COULOMB LAW AND ELECTRIC FIELDExercise:Single Correct
Explore 47 Videos
- COULOMB LAW AND ELECTRIC FIELDBook:CENGAGE PHYSICSChapter:COULOMB LAW AND ELECTRIC FIELDExercise:Multiple Correct
Explore 8 Videos
- COULOMB LAW AND ELECTRIC FIELDBook:CENGAGE PHYSICSChapter:COULOMB LAW AND ELECTRIC FIELDExercise:Exercises
Explore 58 Videos
- COMMUNICATION SYSTEMBook:CENGAGE PHYSICSChapter:COMMUNICATION SYSTEMExercise:QUESTION BANK
Explore 19 Videos
- Current ElectricityBook:CENGAGE PHYSICSChapter:Current ElectricityExercise:QUESTION BANK
Explore 40 Videos
Similar Questions
A ball of radius R carries a positive charge whose volume density depends according only on a separation r from the ball's centre as ρ=ρ0(1−r/R), where ρ0 is a constant. Asumming the permittivites of the ball and the enviroment to be equal to unity find :
(a) the magnitude of the electric field strength as a function of the distance r both inside and outside the ball :
(b) the maximum intensity Emax and the corresponding distance rm.
View SolutionA solid sphere of radius R has a mass distributed in its volume of mass density ρ=ρ0 r, where ρ0 is constant and r is distance from centre. Then moment of inertia about its diameter is
View Solution
Knowledge Check
A sphere of charges of radius R carries a positive charge whose volume chasrge density depends only on the distance r from the ball's centre as ρ=ρ0(1−rR), where ρ0 is constant. Assume epsilon as theh permittivity of space.
the maximum electric field intensity isAEm=ρ0R9εBEm=ρ0ε9RCE_m=(rhoR)/(3epsilon)DEm=ρ0R6εA sphere of charges of radius R carries a positive charge whose volume chasrge density depends only on the distance r from the ball's centre as ρ=ρ0(1−rR), whereρ0 is constant. Assume epsilon as theh permittivity of space.
The magnitude of the electric field as a functiion of the distance r outside the balll is given byAE=ρ0R38εr2BE=ρ0r312εr2CE=ρ0R28εr3DE=ρ0R212εr3A solid sphere of radius R has a volume charge density ρ=ρ0r2 (where ρ0 is a constant ans r is the distance from centre). At a distance x from its centre (for x<R), the electric field is directly proportional to :
A1/x2B1/xCx3Dx2
A ball of radius R carries a positive charge whose volume charge depends only on the distance r from the ball's centre as: ρ=ρ0(1−rR)
Where r0 is a constant. Take ε to be permittivit of the ball. Calculate the maximum electric field intensity at a point (inside or outside the ball) due to such a charge distribution.
View SolutionA ball of radius R has a uniformly distributed charge Q. The surrounding space of the ball is filled with a volume charge density ρ=br , where b is a constant and r is the distance from the centre of the ball. It was found that the magnitude of electric field outside the ball is independent of distance r. (a) Find the value of Q. (b) Find the magnitude of electric field outside the ball.
View SolutionA non-conducting solid sphere has volume charge density that varies as ρ=ρ0 r, where ρ0 is a constant and r is distance from centre. Find out electric field intensities at following positions.
(i) r<R (ii) r≥R
View SolutionA sphere of charges of radius R carries a positive charge whose volume charge density depends only on the distance r from the ball's centre as ρ=ρ0(1−rR), where ρ0 is constant. Assume epsilon as the permittivity of space.
The magnitude of electric field as a function of the distance r inside the sphere is given by
View SolutionA sphere of charges of radius R carries a positive charge whose volume chasrge density depends only on the distance r from the ball's centre as ρ=ρ0(1−rR), where ρ0 is constant. Assume epsilon as theh permittivity of space.
The value of distance rm at which electric field intensity is maximum is given by
View Solution

