An infinte wire having linear charge density λ is arranged as shown in fig. A charge particle of mass m and charge q is released charged q is released from point P. Find the initial acceleration of the particle just after the particle is released.
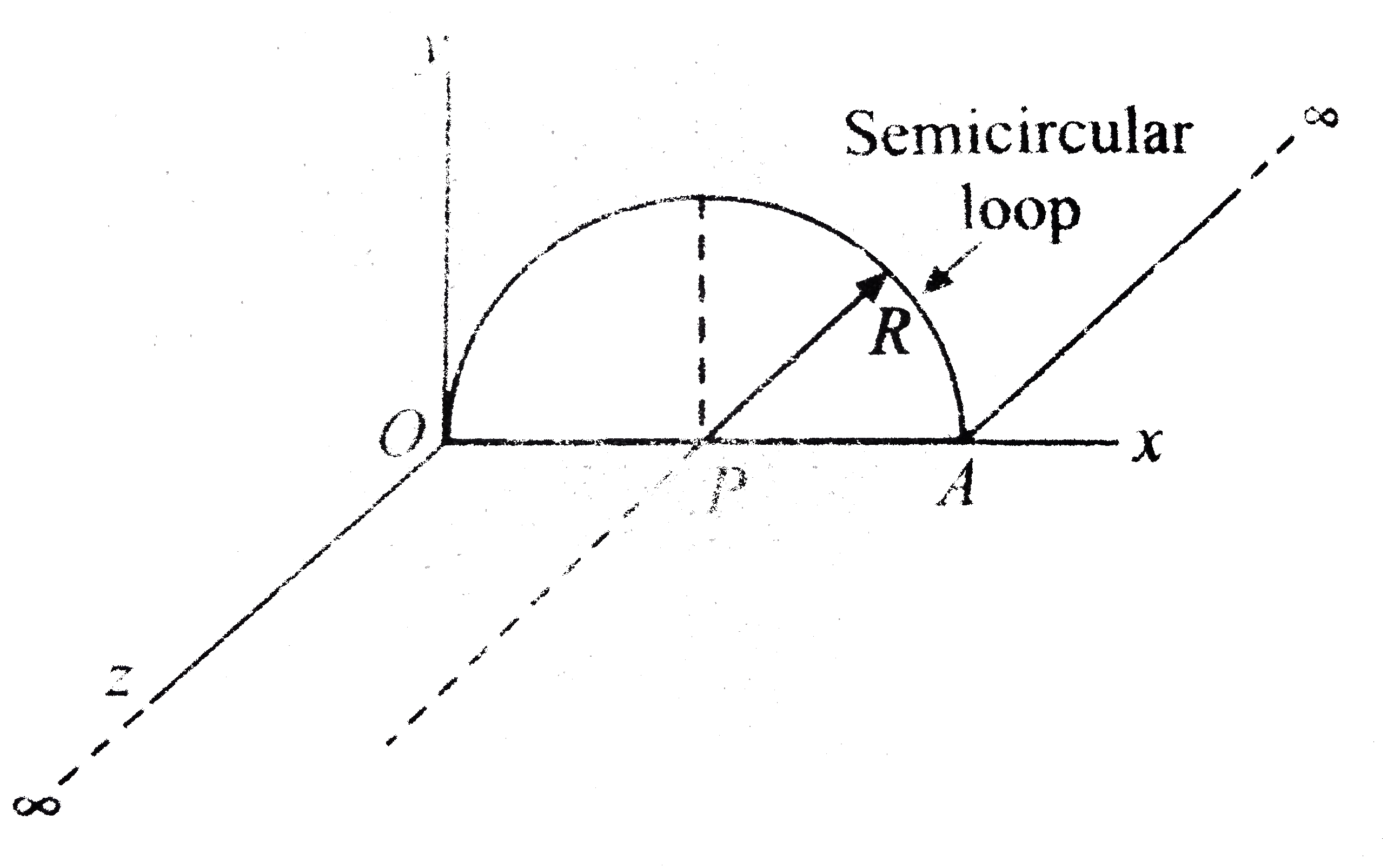
The correct Answer is:−λ2πε0R(−ˆj).
Electric field due to straight wires will cancel out. The net electric field will be due to semicircular wire only. Hence,
→Enet=→Ecircular=λ2πε0R(−ˆj)
so, acceleration is
→a=q→Enetm=qλ2πε0mR(ˆj).
Topper's Solved these Questions
- COULOMB LAW AND ELECTRIC FIELDBook:CENGAGE PHYSICSChapter:COULOMB LAW AND ELECTRIC FIELDExercise:Single Correct
Explore 47 Videos
- COULOMB LAW AND ELECTRIC FIELDBook:CENGAGE PHYSICSChapter:COULOMB LAW AND ELECTRIC FIELDExercise:Multiple Correct
Explore 8 Videos
- COULOMB LAW AND ELECTRIC FIELDBook:CENGAGE PHYSICSChapter:COULOMB LAW AND ELECTRIC FIELDExercise:Exercises
Explore 58 Videos
- COMMUNICATION SYSTEMBook:CENGAGE PHYSICSChapter:COMMUNICATION SYSTEMExercise:QUESTION BANK
Explore 19 Videos
- Current ElectricityBook:CENGAGE PHYSICSChapter:Current ElectricityExercise:QUESTION BANK
Explore 40 Videos
Similar Questions
Electric field E = – bx + a exists in a region parallel to the X direction (a and b are positive constants). A charge particle having charge q and mass m is released from the origin X = 0. Find the acceleration of the particle at the instant its speed becomes zero for the first time after release.
View SolutionA long straight wire carries a charge with linear density λ. A particle of mass m and a charge q is released at a distance r from the the wire. The speed of the particle as it crosses a point distance 2r is
View Solution
Knowledge Check
A charged particle of mass m and charge q is released from rest in an electric field of constant magnitude E. The kinetic energy of the particle after time t is
A2E2t2mqBE2q2r22mCEq2m2t2DEqm2tA charged particle of mass m and charge q is released from rest in an electric field of constant magnitude E. The kinetic energy of the particle after time t is
A2E2t2mqBE2q2t22mCEq2m2t2DEqm2tIf linear charge density of a wire as shown in the figure is λ
 Apotential at the centre is λ2ε0Belectric field at the centre of the loop is λ2πε0RCelectric field at the centre of the loop is λ2πε0R+λ2ε0RDNone of the above
Apotential at the centre is λ2ε0Belectric field at the centre of the loop is λ2πε0RCelectric field at the centre of the loop is λ2πε0R+λ2ε0RDNone of the above
A charged particle of mass m and charge e is released from rest in an electric field of constant magnitude E. The kinetic energy of the particle after time t is Ek and the linear momentum is p. We have
View SolutionA charged particle of mass m and charge e is released from rest in an electric field E. If kinetic energy of particle after time t is Ek and linear momentum is p, then
View SolutionA charged particle of mass m and charge q is released from rest the position (x0,0) in a uniform electric field E0ˆj. The angular momentum of the particle about origin.
View SolutionA particle of mass m and charge q is placed at rest in a uniform electric field E and then released, the kinetic energy attained by the particle after moving a distance y will be
View SolutionA long solenoid carrying a current I is placed with its axis vertical as shown in the figure. A particle of mass m and charge q is released from the top of the solenoid. Its acceleration is (g being acceleration due to gravity)
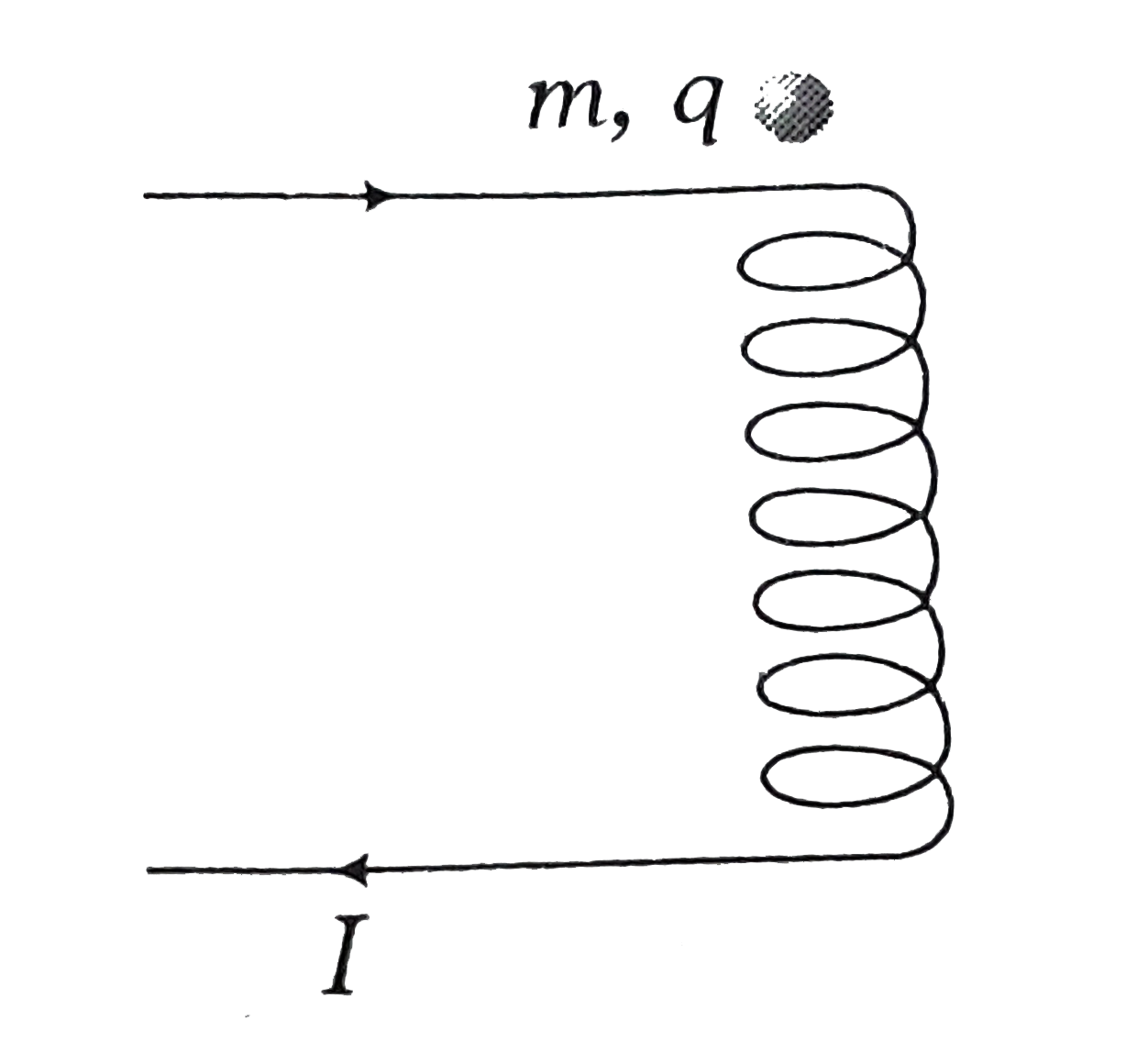
View Solution

