A thin rigid insulated rod of mass m and length l carrying a charge Q unformly distrivuted along its length is smoothly pivoted at P. It is palced in between the charged large conducting plates. Disregard gravity.
(a) Find the initial accelaeration of the rod.
(b) Find the angular speed of the rod as the function of angel of rotation , if the rod is allowed to rotate freely .

The correct Answer is:(a) (b)
(a)
 ,
,
(b) Work done by F=KE gained by the rod
or,
or .
Topper's Solved these Questions
- COULOMB LAW AND ELECTRIC FIELDBook:CENGAGE PHYSICSChapter:COULOMB LAW AND ELECTRIC FIELDExercise:Single Correct
Explore 47 Videos
- COULOMB LAW AND ELECTRIC FIELDBook:CENGAGE PHYSICSChapter:COULOMB LAW AND ELECTRIC FIELDExercise:Multiple Correct
Explore 8 Videos
- COULOMB LAW AND ELECTRIC FIELDBook:CENGAGE PHYSICSChapter:COULOMB LAW AND ELECTRIC FIELDExercise:Exercises
Explore 58 Videos
- COMMUNICATION SYSTEMBook:CENGAGE PHYSICSChapter:COMMUNICATION SYSTEMExercise:QUESTION BANK
Explore 19 Videos
- Current ElectricityBook:CENGAGE PHYSICSChapter:Current ElectricityExercise:QUESTION BANK
Explore 40 Videos
Similar Questions
A charge Q is uniformly distributed on the rod of length L which is pivoted at one of its end. The rod is kept between two plates having charge densities o and-o. The initial angular acceleration of the rod is (mass of rod = M) + 0 o
View SolutionA uniform rod of mass m and length l is pivoted smoothly at O. A horizontal force acts at the bottom of the rod.
a. Find the angular velocity of the rod as the function of angle of rotation θ.
b.What is the maximum angular displacement of the rod?

View Solution
Knowledge Check
A uniform rod of mass M and length L carrying a charge q uniformly distributed over its length is rotated with constant velocity w about its mid point perpendicular to the rod. Its magnetic moment is
AqωL2/6BqωL2/12CqωL2/24DqωL2/48An insulating rod of length I carries a charge q distrubuted uniformly on it. The rod is pivoted at its mid-point and is rotated at a frequency f about a fixed axis perpendicular to the the rod and passing through the pivot . The magnetic moment of the rod system is
A112πqfl2Bπqfl2C16πqfl2D13πqfl2
A charge Q is uniformly distributed on the rod of length L which is pivoted at one of its end. The rod is kept between two plates having charge densities sigma and -sigma. The initial angular acceleration of the rod is (mass of rod=M) +sigma + + 0 + = 声 (は) (1)/(4)
View SolutionA rod has a total charge Q uniformly distributed along its length L. If the rod rotates with angular velocity ω about its end, compute its magnetic moment.

View Solutiona point charge q is situated at a distance r from one end of a thin conduction rod of length L having a charge Q (unifromly distributed a long its length).find the magnitudes of electric froce between the two.
View SolutionA ligh rod of length 1 m is pivoted at its centre and two masses of 5 kg and 2 kg are hung from the ends as shown in the figure. Find the initial angular acceleration of the rod assuming that it was horizontal in the beginning.

View SolutionA conductor (rod) of mass m, length l carrying a current i is subjected to a magnetic field of induction B. If the coefficients of friction between the conducting rod and rail is μ, find the value of I if the rod starts sliding.
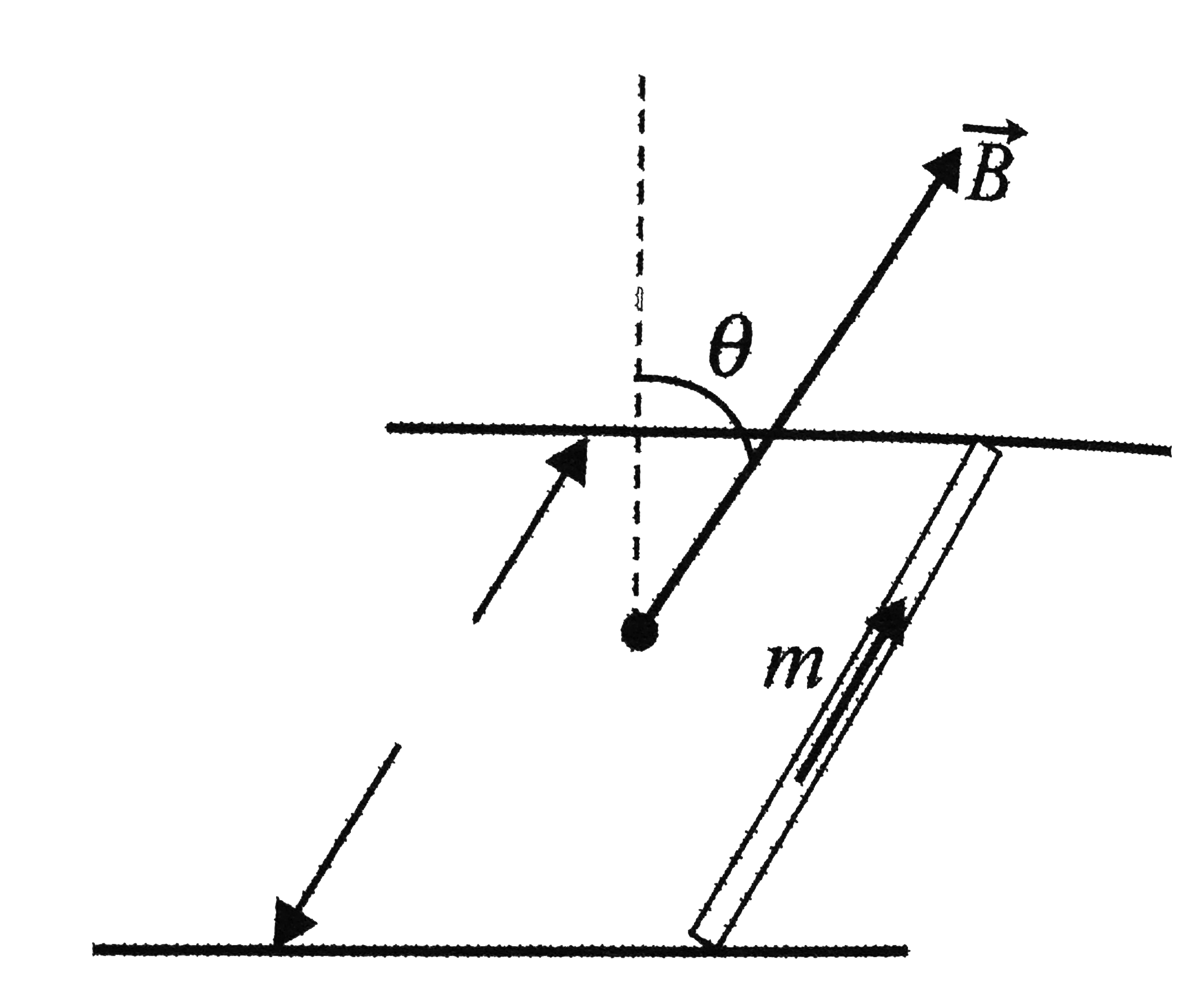
View SolutionA uniform rod of length L and mass M is free to rotate about a frictionless pivot at one end. The rod is released from rest in the horizontal position. What are the initial angular acceleration of the rod and the initial linear acceleration of the right end of the Rod ?
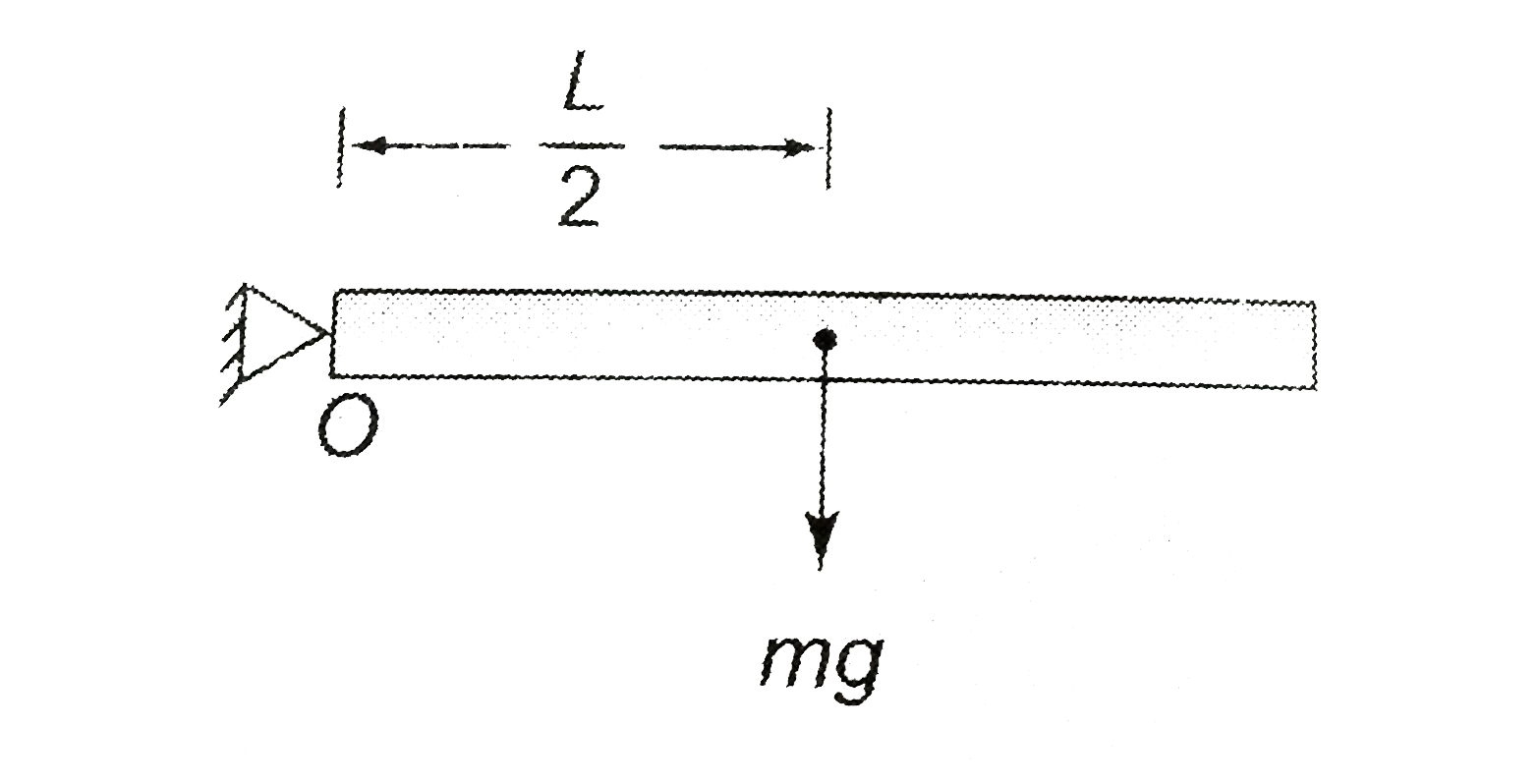
View Solution

