Two semicircle wires ABC, and ADC, each of radius R are lying on xy and xz planes, respectively as shown in fig.
if the linear charge density of the semicircle parts and straight parts and straight parts is λ, Find the electric field entensity →E at the origin .

The correct Answer is:−λ2πε0R(ˆj+ˆk).
Electric field due to MA: →E1=λ4πε0R(ˆi−ˆk)
Electric field due to ADC: →E2=λ2πε0R(−ˆk)
Electric field due to ABC: →E3=λ2πε0R(−ˆj)
Electric field due to NC: →E4=λ4πε0R(ˆi−ˆk)
Net electric field is
→E0=→E1+→E2+→E3+→E4=−λ2πε0R(ˆj+ˆk).
Topper's Solved these Questions
- COULOMB LAW AND ELECTRIC FIELDBook:CENGAGE PHYSICSChapter:COULOMB LAW AND ELECTRIC FIELDExercise:Single Correct
Explore 47 Videos
- COULOMB LAW AND ELECTRIC FIELDBook:CENGAGE PHYSICSChapter:COULOMB LAW AND ELECTRIC FIELDExercise:Multiple Correct
Explore 8 Videos
- COULOMB LAW AND ELECTRIC FIELDBook:CENGAGE PHYSICSChapter:COULOMB LAW AND ELECTRIC FIELDExercise:Exercises
Explore 58 Videos
- COMMUNICATION SYSTEMBook:CENGAGE PHYSICSChapter:COMMUNICATION SYSTEMExercise:QUESTION BANK
Explore 19 Videos
- Current ElectricityBook:CENGAGE PHYSICSChapter:Current ElectricityExercise:QUESTION BANK
Explore 40 Videos
Similar Questions
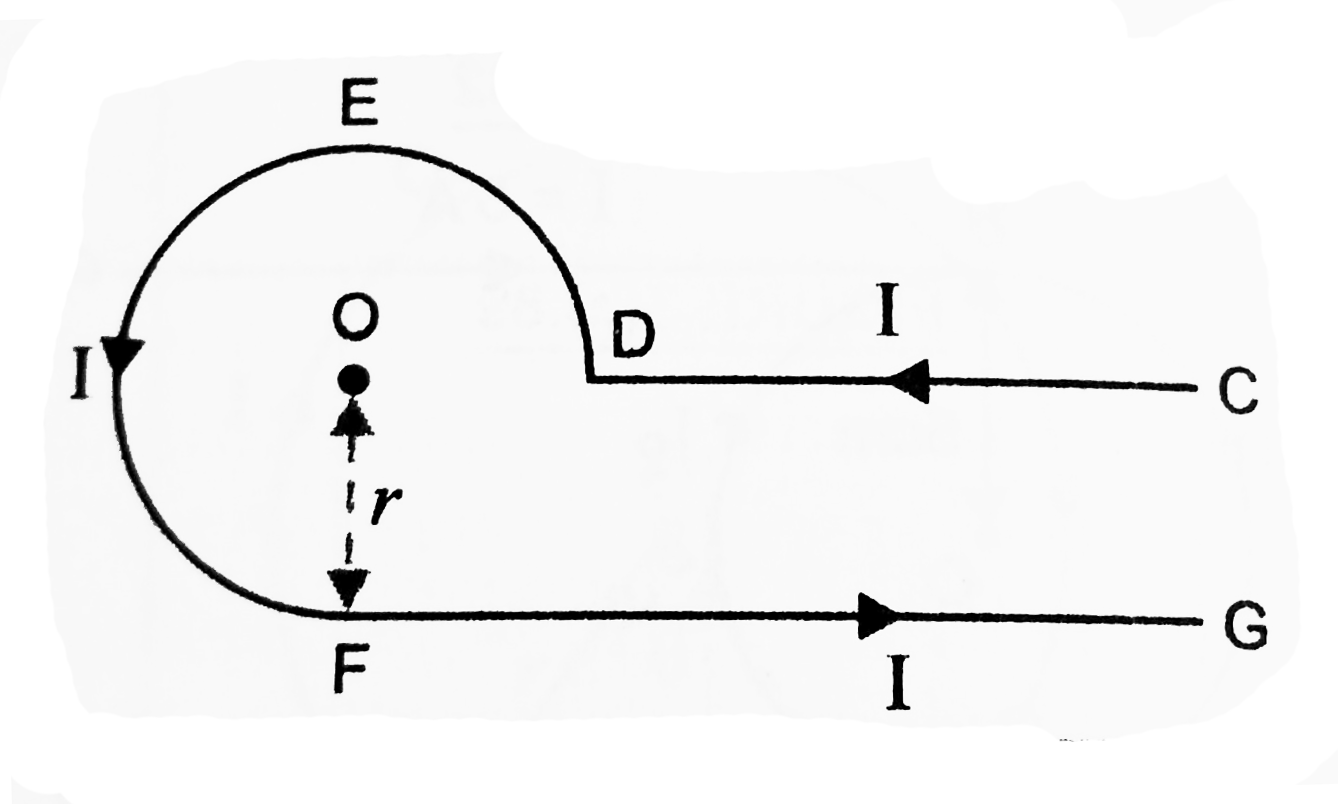
A current I is flowing in a conductor shaped as shown in figure. The radius of the curved part is r and length of straight portion is very large. Find the magnetic field induction at the centre O.
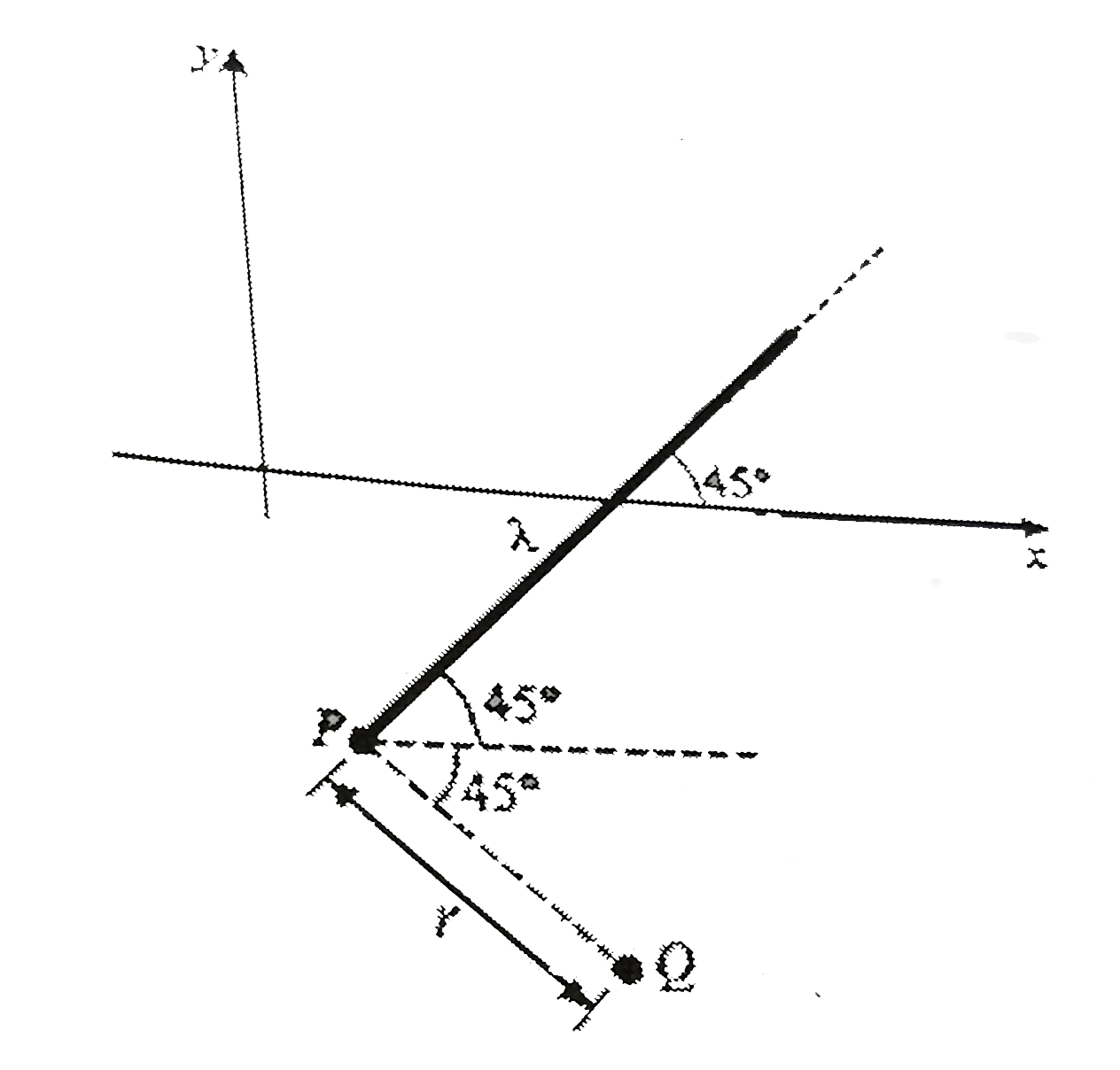
View SolutionA very long charged wire (lying in the xy plane ) which is having a linear charge density λ is having one of its end at a point P as shown in figure . What is electric field intensity at point Q :
View Solution
Knowledge Check
An infinitely long wire with linear charge density +λ is bent and the two parts are inclined at angle 30∘ as shown in fig, the electric field at point P is :
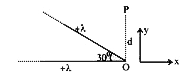 Aλ4π∈0d[(1+√3)ˆi+ˆj]Bλ4π∈0d[(1−√3)ˆi+2ˆj]Cλ4π∈0d[(1+√3)ˆi−2ˆj]Dλ4π∈0d[(1+√3)ˆi+2ˆj]
Aλ4π∈0d[(1+√3)ˆi+ˆj]Bλ4π∈0d[(1−√3)ˆi+2ˆj]Cλ4π∈0d[(1+√3)ˆi−2ˆj]Dλ4π∈0d[(1+√3)ˆi+2ˆj]A wire is bent to form a semi circle such that the radius of the semicircle is R. The charge per unit length is λ. The total electric field at the centre will be
A2λ/πε0RBλ/2πε0RC2λ/πε0R2Dλ/πε20RCurrent I is flowing in a conductor shaped as shown in the figure. The radius of the curved part is r and the length of straight portion is very large. The value of the magnetic field at the centre will be
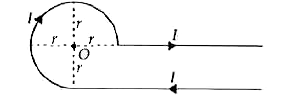 Aμ04πr(π2+1)Bμ04πr(π2−1)Cμ04πr(3π2+1)Dμ04πr(3π2−1)
Aμ04πr(π2+1)Bμ04πr(π2−1)Cμ04πr(3π2+1)Dμ04πr(3π2−1)
A long wire with a uniform charge density λ is bent in two configurations shown in fig. Determine the electric field intensity at point O.
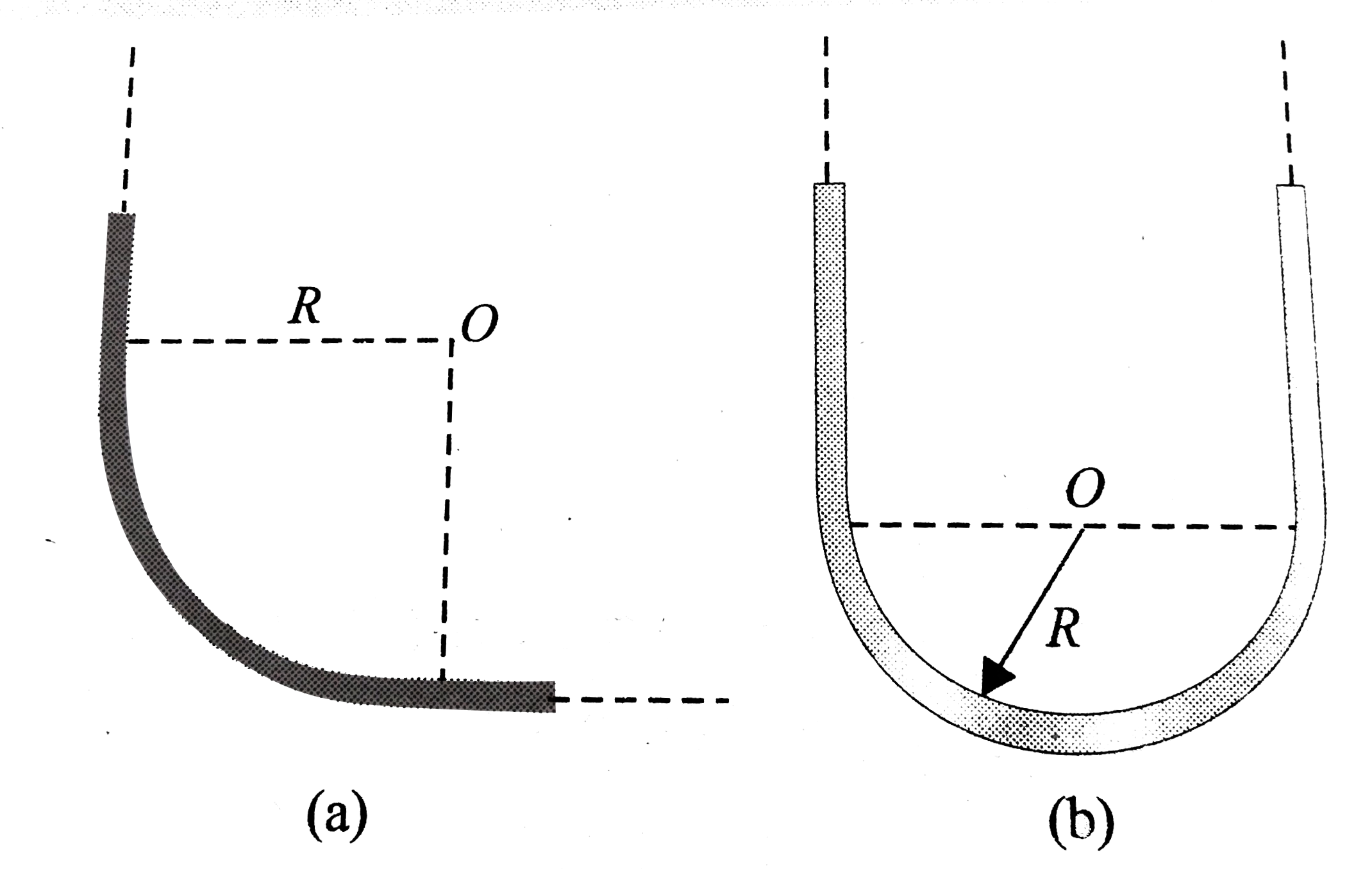
View SolutionA uniformly charged disc of radius R having surface charge density σ is placed in the xy plane with its center at the origin. Find the electric field intensity along the z-axis at a distance Z from origin :
View SolutionTwo long wires having linear charge density λ and −λ are placed parallel to each other at separation ras shown in the figure. The electric field at point P will be
View SolutionA ring of radius R is marked in six equal parts and these parts are charged uniformly each with a charge of magnitude Q but positive and negative alternately as shown. The electric field at centre of ring will be
View SolutionA semicircle conducting ring of radius R is placed in the xy plane, as shown in Fig. A uniform magnetic field is set up along the x-axis. No emf, will be induced in the ring if

View Solution

