A rod has a total charge Q uniformly distributed along its length L. If the rod rotates with angular velocity $ω$ about its end, compute its magnetic moment.

Video Solution

Text Solution

Verified by Experts

We can visualize the rod to consist of differential element dQ, which constitute a series of concentric current loop. The charge per unit length of the rod is $λ$ ,
$λ = \frac{Q}{L}$
So the charge on a differential element of length dl,
$d q = λ d l$
The current $d l$ due to rotation of this charge is given by
$d I = \frac{d q}{(2 \frac{π}{o} m e n g a)} = \frac{ω}{2 π} d q = \frac{ω}{2 π} λ d l$

The magnetic moment of this differential current loop,
$d M = d I (π l^{2}) = (\frac{ω}{2 π} λ d l) π l^{2} = \frac{ω λ}{2} l^{2} d l$
To find total magnetic moment, we integrate
$M = \frac{ω λ}{2} \int + 0^{L} l^{2} d l = \frac{ω λ L^{3}}{6}$
Subtituting for $λ$ , we obtain $M = \frac{Q ω L^{2}}{6}$ .

|

Updated on:21/07/2023

Class 12 PHYSICS MOVING CHARGES AND MAGNETISM

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One or More
A uniform rod of mass M and length L carrying a charge q uniformly distributed over its length is rotated with constant velocity w about its mid point perpendicular to the rod. Its magnetic moment is
A $q ω L^{2} / 6$
B $q ω L^{2} / 12$
C $q ω L^{2} / 24$
D $q ω L^{2} / 48$
Question 2 - Select One
Consider the situation shown in the figure of the previous problem. Suppose the wire connecting O and C has zero resistance but the circular loop has a resistance R uniformly distributed along its length. The rod OA is made to rotate with a uniform angular speed $(ω)$ as shown in the figure. Find the current in the rod when $- A O C = 90^{\circ}$
A $\frac{5}{3} \frac{B a^{2} ω}{R}$
B $\frac{8}{3} \frac{B a^{2} ω}{R}$
C $\frac{B a^{2} ω}{3 R}$
DNone of these
Question 3 - Select One
A disc of mass $m$ has a charge $Q$ distributed on its surface. It is rotating about an $X X'$ with a angular velocity $ω$ . The force acting on the disc is

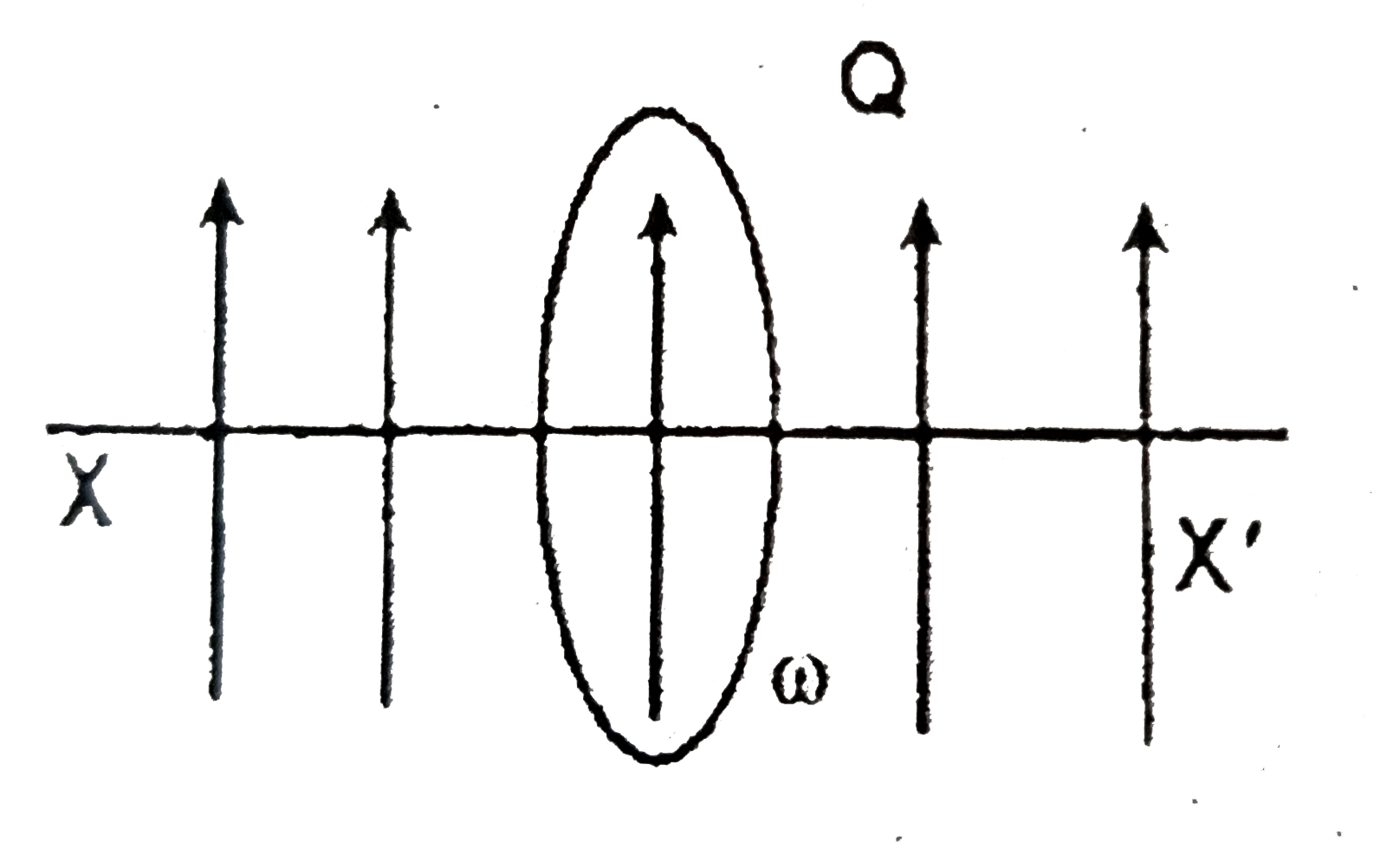Azero
B $ω R B / π$
C $2 Q ω B R$
Dnone of these

CENGAGE PHYSICS-MAGNETIC FIELD AND MAGNETIC FORCES-Exercise1.3

Home
Ask Doubt
Profile