Question

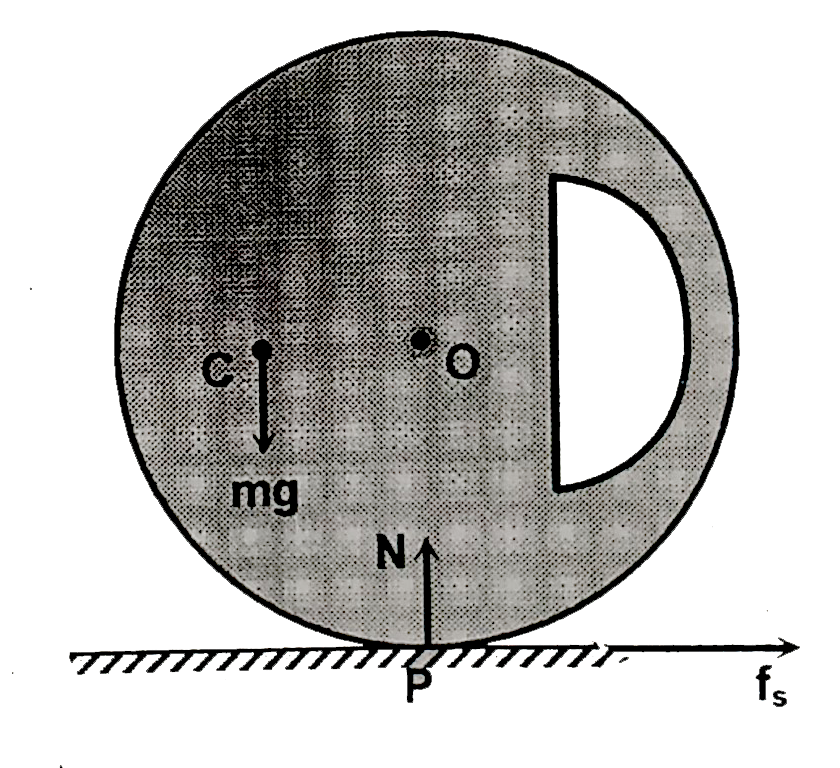
A disc shaped body (having a hole shown in the figure) of mass $m=10kg$ and radius $R=\frac{10}{9}m$ is performing pure rolling motion on a rough horizontal surface. In the figure point $O$ is geometrical center of the disc and at this instant the centre of mass $C$ of the disc is at same horizontal level with $O$. The radius of gyration of the disc about an axis pasing through $C$ and perpendicular to the plane of the disc is $\frac{R}{2}$ and at the insant shown the angular velocity of the disc is $\omega =\sqrt{\frac{g}{R}}$ rad/sec in clockwise sence. $g$ is gravitation acceleration $=10m/s^2$. Find angular acceleation $\alpha$ ( in $rad/s^2$) of the disc at this instant.

Answer

6

Explanation

Considering torque of real and pseudo force in the frame of `P`,
`tau=mg R/2+m omega^(2) R R/2`
`=mg R/2 + m g/R R R/2 = mgR`
`I_(P)=m(R/2)^(2)+m(R^(2)+(R^(2))/4)=3/2 mR^(2)`
`:. alpha=(2mgR)/(3mR^(2))=(2g)/(3R)=6 rad//s^(2)`