A uniform conducting ring of mass m=2kg, radius r=2m and resistance 8Ω is kept on smooth, horizontal surface. A time varying magnetic field →B=(ˆi+t2ˆj) Tesla is present in the region, where t is time in second and take vertical as y-axis. (Take π2=10). Then
Time when ring starts toppling is 1 sec
Time when ring starts toppling is 3/4 sec
Heat generated through the ring till the instant when the ring start toppling is 40/3 Joule.
Heat generated through the ring till the instant when the ring start toppling is 80/3 Joule
The correct Answer is:A, D
ϕ=BA=(t2)(πr2)
ε=dϕdt=2πr2t
i=εR=2πr2tR
For toppling
τ=∣∣→μ×→B∣∣≥mgr
(i.πr2).1≥mgr
2πr2tR.πr2≥mgr
t≥mgR2π2r3=1sec
Heat =∫i2Rdt=∫(2πr2tR)2=dt.R
Heat =4π2r4R∫10t2dt=803 Joule
Topper's Solved these Questions
- TEST PAPERSBOOK - FIITJEECHAPTER - TEST PAPERSEXERCISE - PHYSICS
747 Videos
- SIMPLE HARMONIC MOTIONBOOK - FIITJEECHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Assignment Problems (Objective) (Level-II)
20 Videos
- WORK, ENERGY AND POWER BOOK - FIITJEECHAPTER - WORK, ENERGY AND POWER EXERCISE - COMPREHENSIONS ( Comprehension-II)
5 Videos
Similar Questions
A conducting ring of radius r and resistance R is placed in region of uniform time varying magnetic field B which is perpendicular to the plane of the ring. It the magnetic field is changing at a rate α, then the current induced in the ring is
View SolutionA conducting ring of mass m=πkg and radius R=12m is kept on a flat horizontal surface (xy plane). A uniform magnetic field is switched on in the region which changes with time (t) as →B=(2ˆj+t2ˆk)T. Resistance of the ring is r=πΩ and g=10ms−2.
(a) Calculate the induced electric field at the circumference of the ring at the instant it begins to topple.
(b) Calculate the heat generated in the ring till the instant it starts to topple.

View Solution
Knowledge Check
A uniform conducting ring of mass π kg and radius 1 m is kept on smooth horizontal table. A uniform but time varying magnetic field B=(ˆi+t2ˆj)T is present in the region, where t is time in seconds. Resistance of ring is 2(Ω). Then
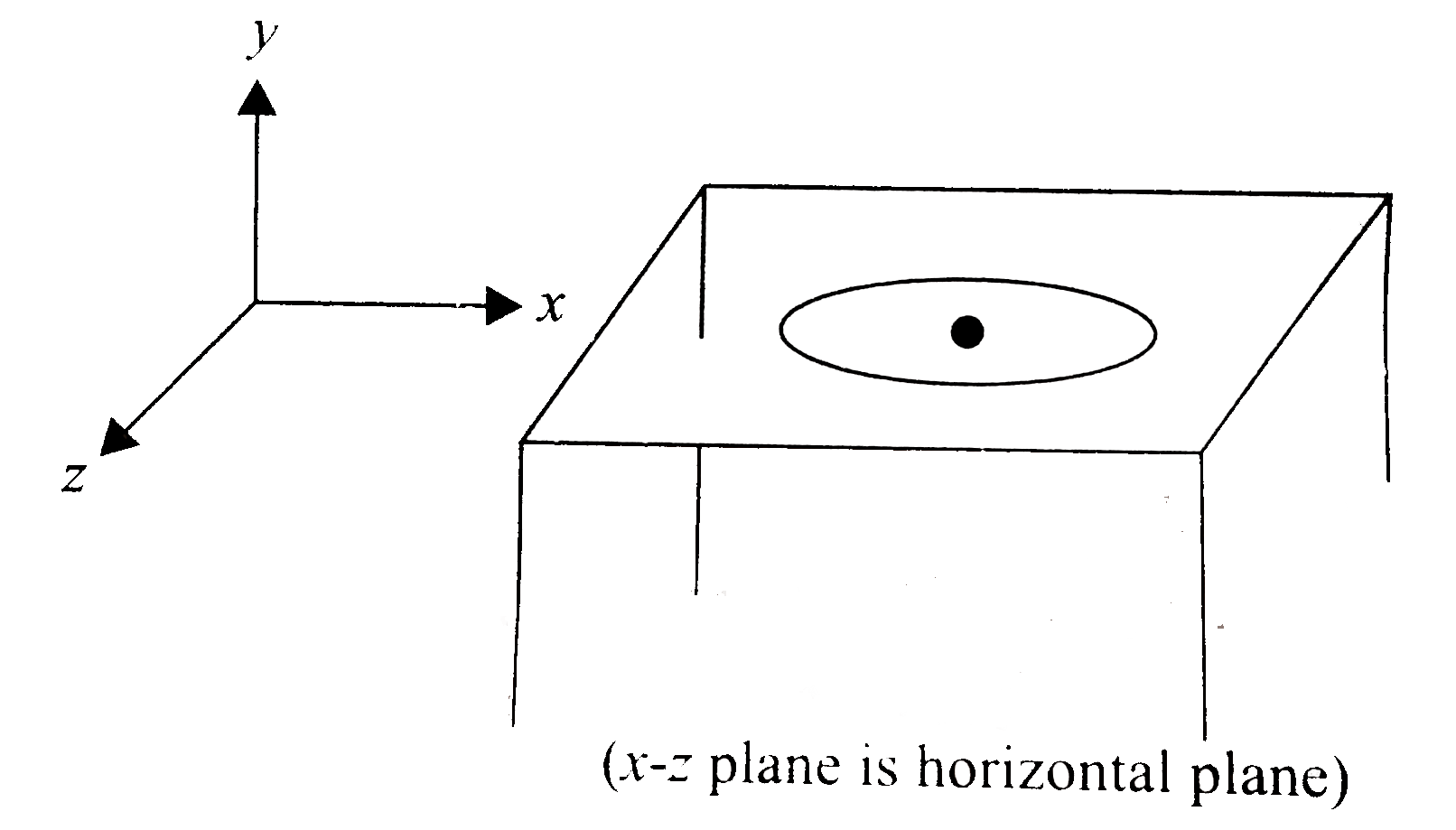
Net magnetic field (in Newton) on conducting ring as function of time isA2π2tB2π2t2C2π2t3DzeroA uniform conducting ring of mass π kg and radius 1 m is kept on smooth horizontal table. A uniform but time varying magnetic field B=(ˆi+t2ˆj)T is present in the region, where t is time in seconds. Resistance of ring is 2(Ω). Then
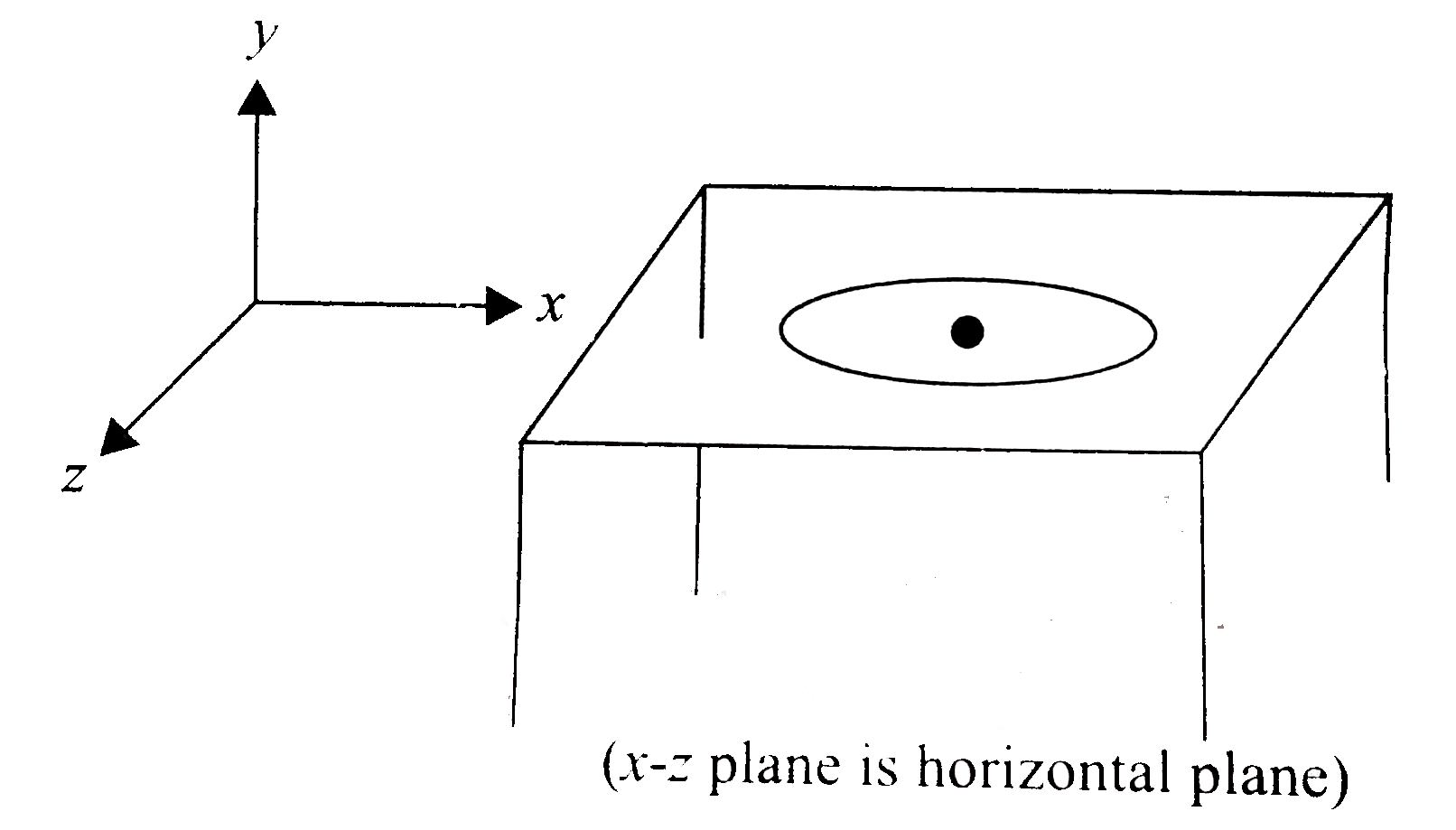
Time (in second) at which ring start toppling isA10πB20πC5πD25πA uniform conducting ring of mass π kg and radius 1 m is kept on smooth horizontal table. A uniform but time varying magnetic field B=(ˆi+t2ˆj)T is present in the region, where t is time in seconds. Resistance of ring is 2(Ω). Then
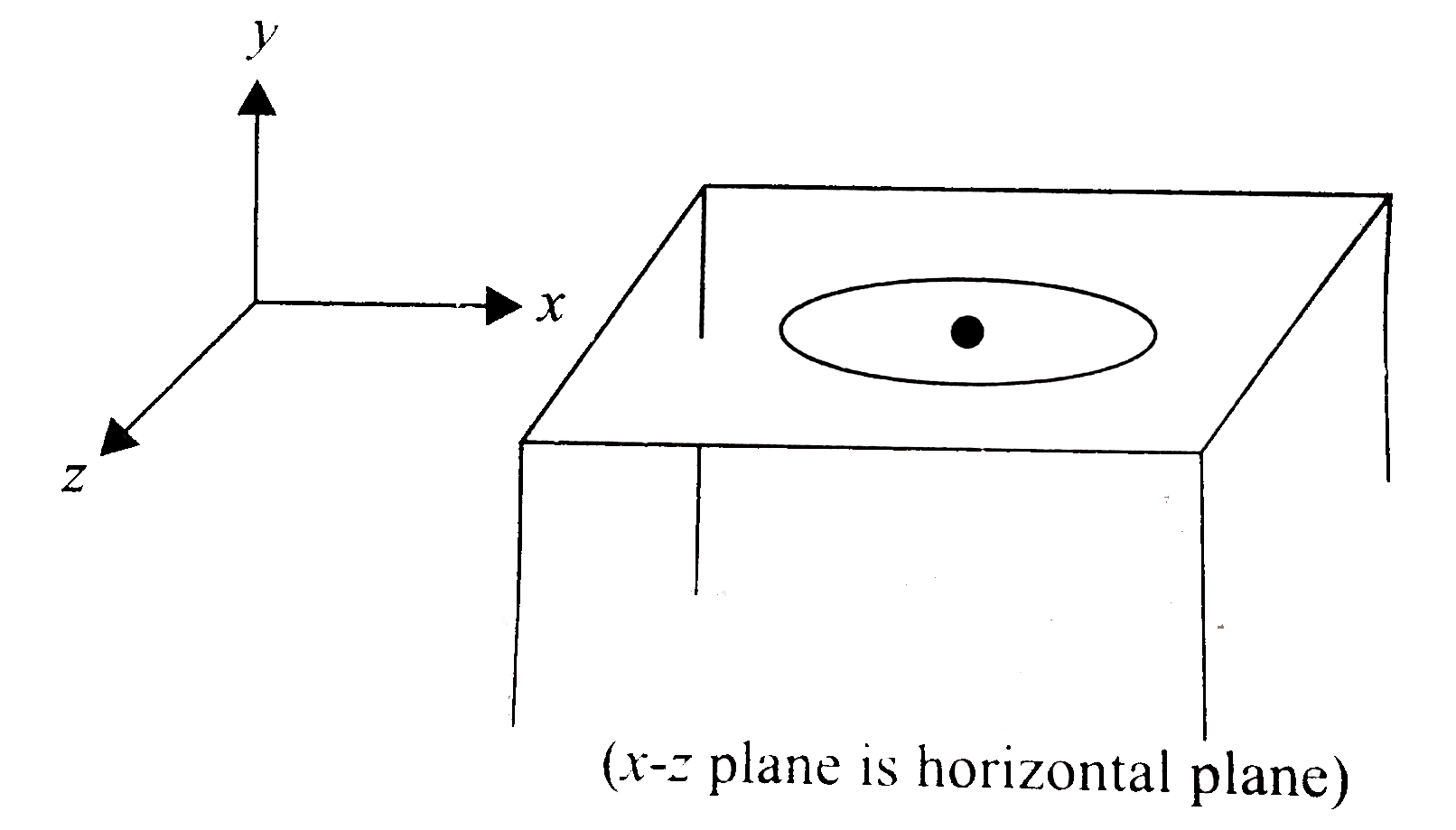
Induced electric field (in volt/meter) at the circumference of ring at the instant ring start toppling isA10πB20πC5πD25π
A conducting ring of mass 2 kg and radius 0.5 m is placed on a smooth horizontal plane. The ring carries a current 4A . A horizontal magnetic field B = 10T is switched on at time t = 0 as shown in figure. The initial angular acceleration of the ring will be:

View SolutionA charged ring of mass m = 50 gm, charge 2 coulomb and radius R = 2m is placed on a smooth horizontal surface. A magnetic field varying with time at a rate of (0.2 t) Tesla/sec is applied on to the ring in a direction normal to the surface of ring. Find the angular speed attained in a time t1=10sec.
View SolutionA uniform conducting ring of mass π kg and radius 1 m is kept on smooth horizontal table. A uniform but time varying magnetic field B=(ˆi+t2ˆj)T is present in the region, where t is time in seconds. Resistance of ring is 2(Ω). Then
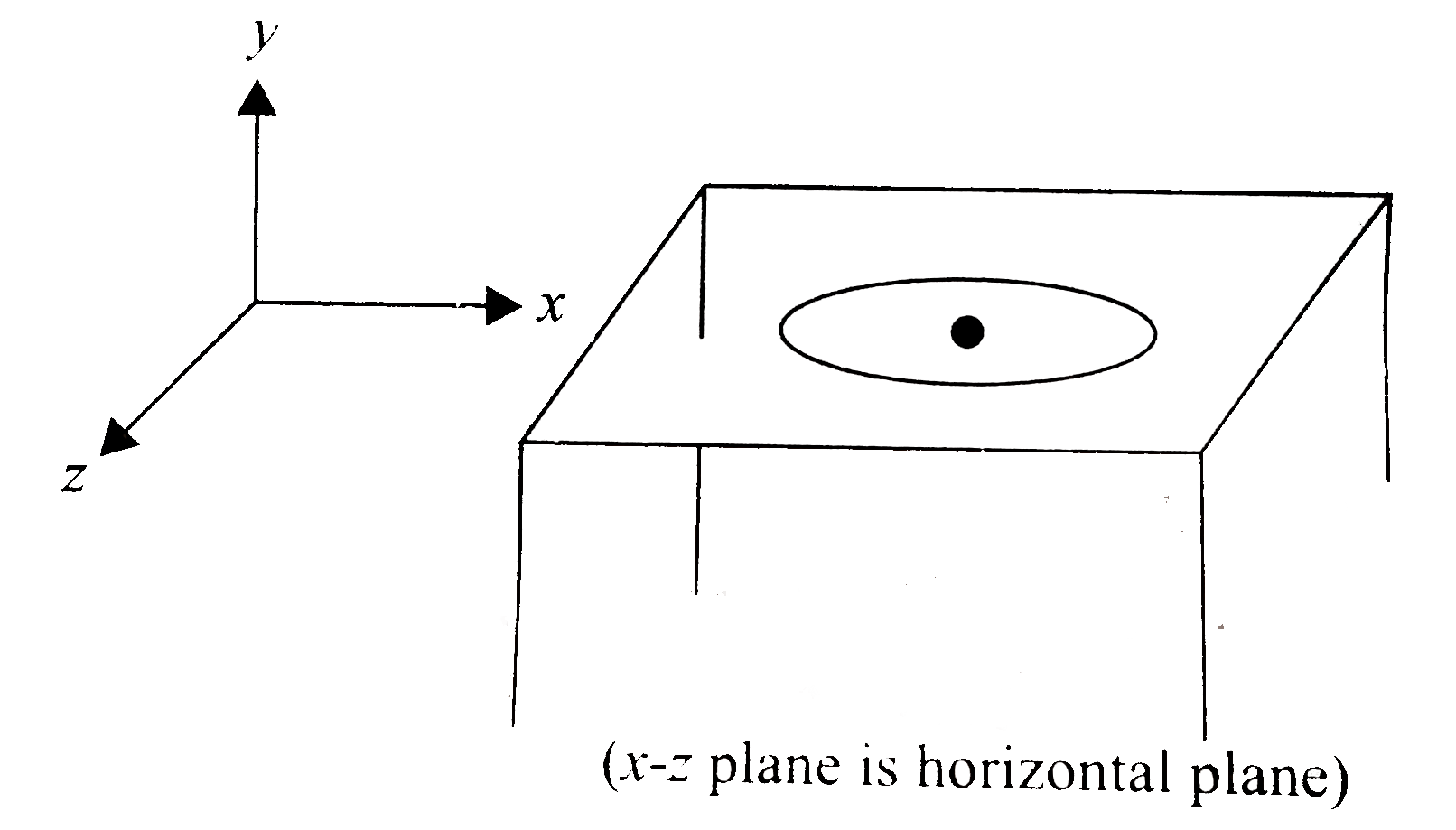
Heat generated (in kJ) through the ring till the instant when ring start toppling is
View SolutionA conducting circular loop of raidus and resistance R is kept on a horiozntel plane. A vertical time varing magnetic field B=2t is switched on at time t=0. Then
View SolutionA conducting ring of radius 2R rolls on a smooth horizontal conducting surface as shown in figure-5.295. A uniform horizontal magnetic field B is perpendicular to the plane of the ring. The potential of A with respect to O is:

View Solution
