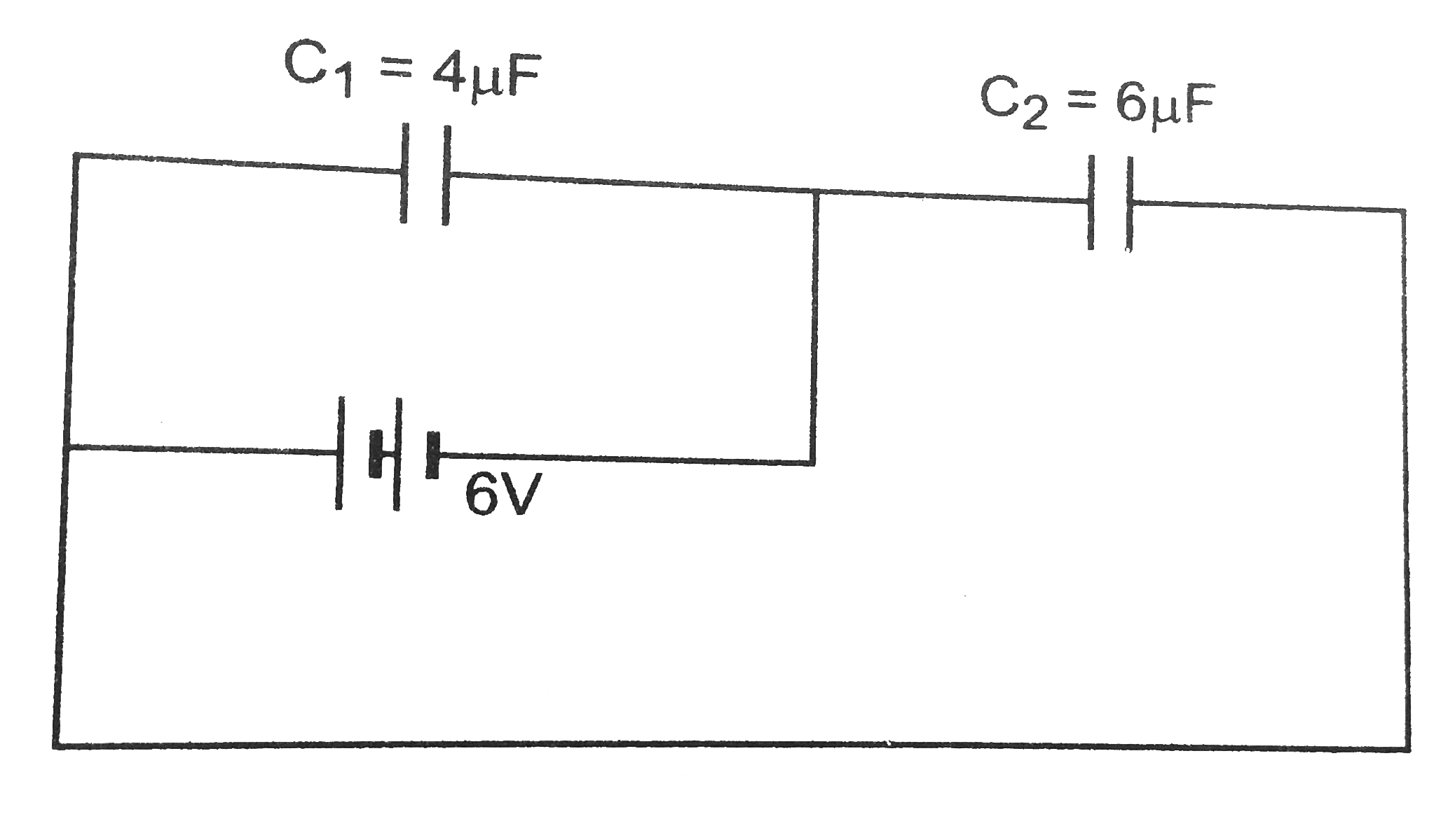
Three capacitor C1=6F,C2=3F and C3=4F are separately charged with battery such that charge on each capacitor are 36C,24C and 40C respectively and then disconnected with the battery. After that they are connected in a circuit along with an uncharged capacitor C4=4F and a battery of emf =4 volts as shown figure. Now the switch S is closed. Choose is correct option (s).
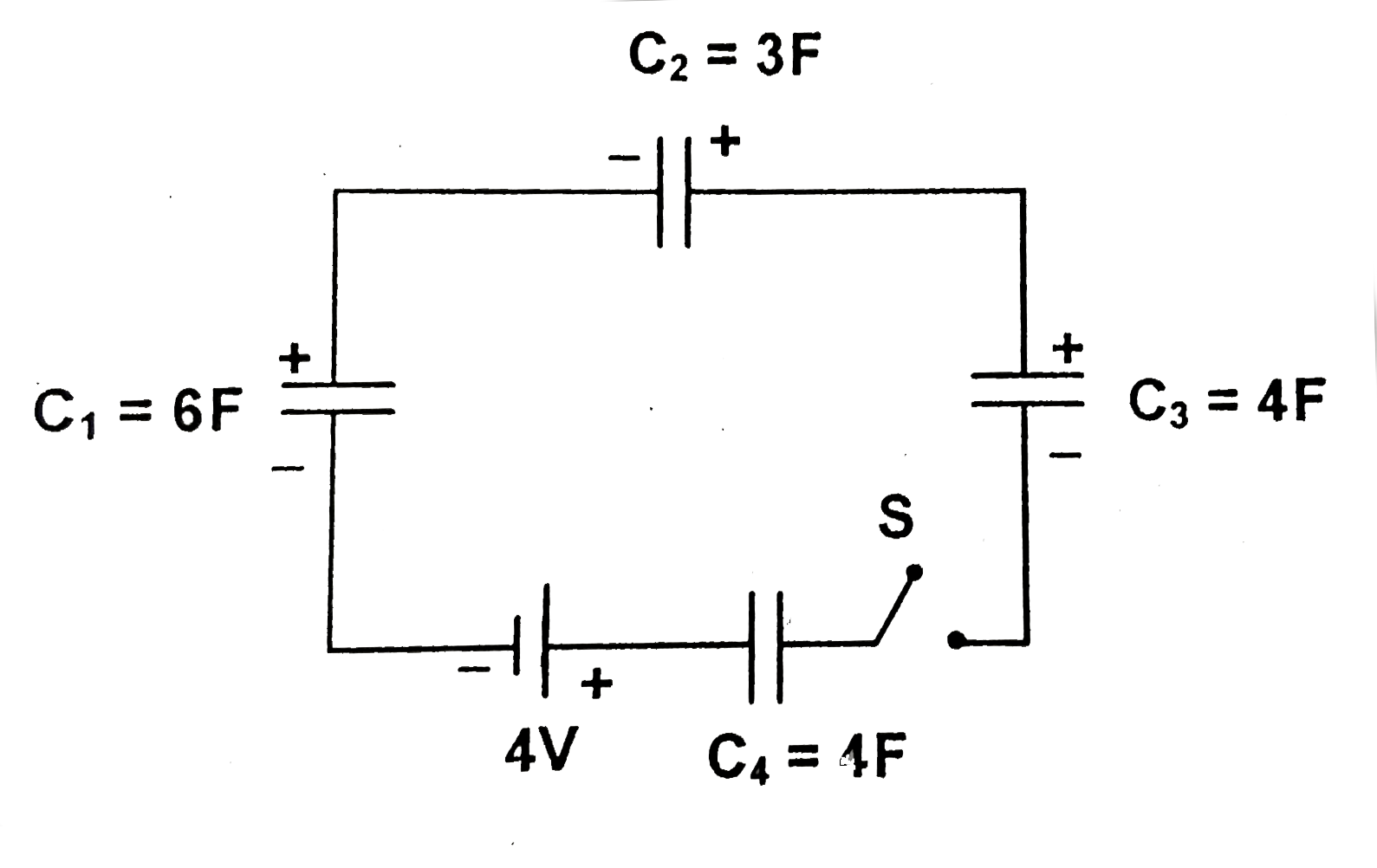
Final charge on capacitor C4=4C
Final charge on capacitor C2=24C
Final charge on capacitor C3=36C
Amount of charge flow in circuit = zero
The correct Answer is:B, D
By applying Kirchhoff's law
−4+q4+−40+q4+24+q3+36+q6=0
−4+q4−10+q4+8+q3+6+q6=0
q4+14+13+16=0
⇒q=0
Hence, there is no flow of charge.
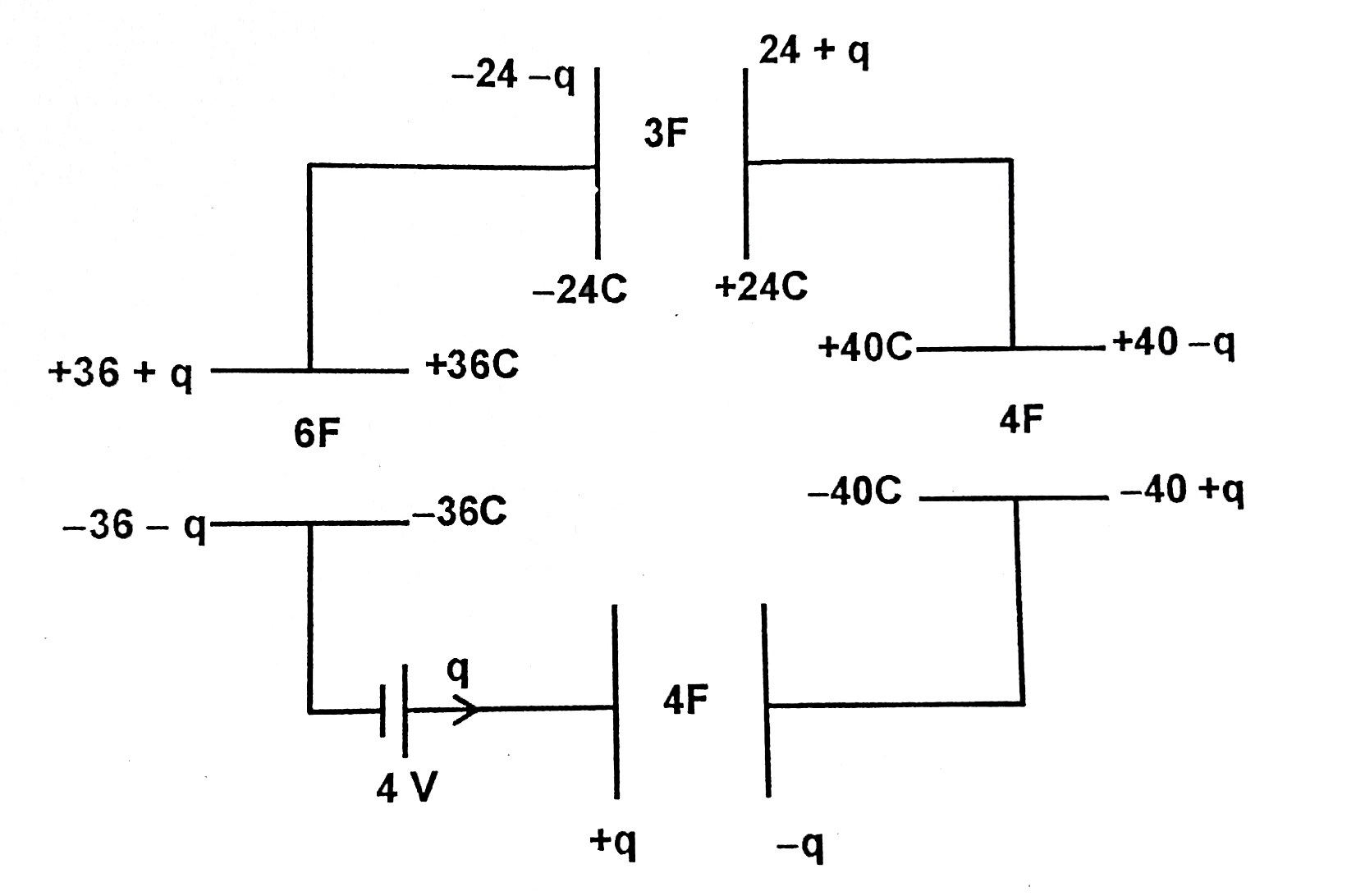
Topper's Solved these Questions
- TEST PAPERSBOOK - FIITJEECHAPTER - TEST PAPERSEXERCISE - PHYSICS
747 Videos
- SIMPLE HARMONIC MOTIONBOOK - FIITJEECHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Assignment Problems (Objective) (Level-II)
20 Videos
- WORK, ENERGY AND POWER BOOK - FIITJEECHAPTER - WORK, ENERGY AND POWER EXERCISE - COMPREHENSIONS ( Comprehension-II)
5 Videos
Similar Questions
Knowledge Check
Two capacitor C1 and C2, charged with chargesq1 and q2 then these are connected in series with an uncharged capacitor C, as shown in figure. As the switch S is closed :
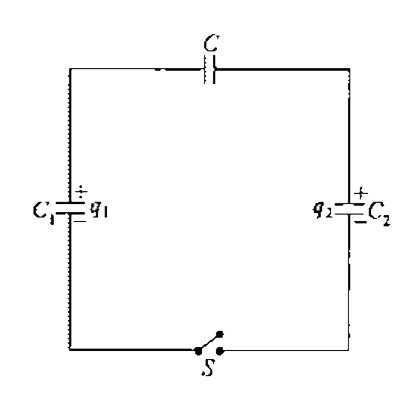 AC gets charged in any conditionBC gets charged only when q1C2>q2C1CC gets charged only when q1C2<q2C1DC gets chharged when q1C2≠q2C1
AC gets charged in any conditionBC gets charged only when q1C2>q2C1CC gets charged only when q1C2<q2C1DC gets chharged when q1C2≠q2C1Three capacitors A , B and C are connected to a battery of 25volt as shown in the figure. The ratio of charges on capacitors A
 A5:2:3B5:3:2C2:5:3D2:3:5
A5:2:3B5:3:2C2:5:3D2:3:5A capacitor of capacitance C1 is charged to a potential difference V and then connected with an uncharged capacitor of capacitance C2 a resistance R. The switch is closed at t = 0. Choose the correct option(s):
AThe initial current through the resistance is VRBThe current through the resistance as a function of time is i(t)=VRe−tτ where τ=R(C1C2C1+C2)CThe charge on capacitor C1 as a function of time is q1(t)=(C1VC1+C2)(C1+C2e−tτ)DAfter a long time, the potential difference across the capacitor C1is(C1C1+C2)V
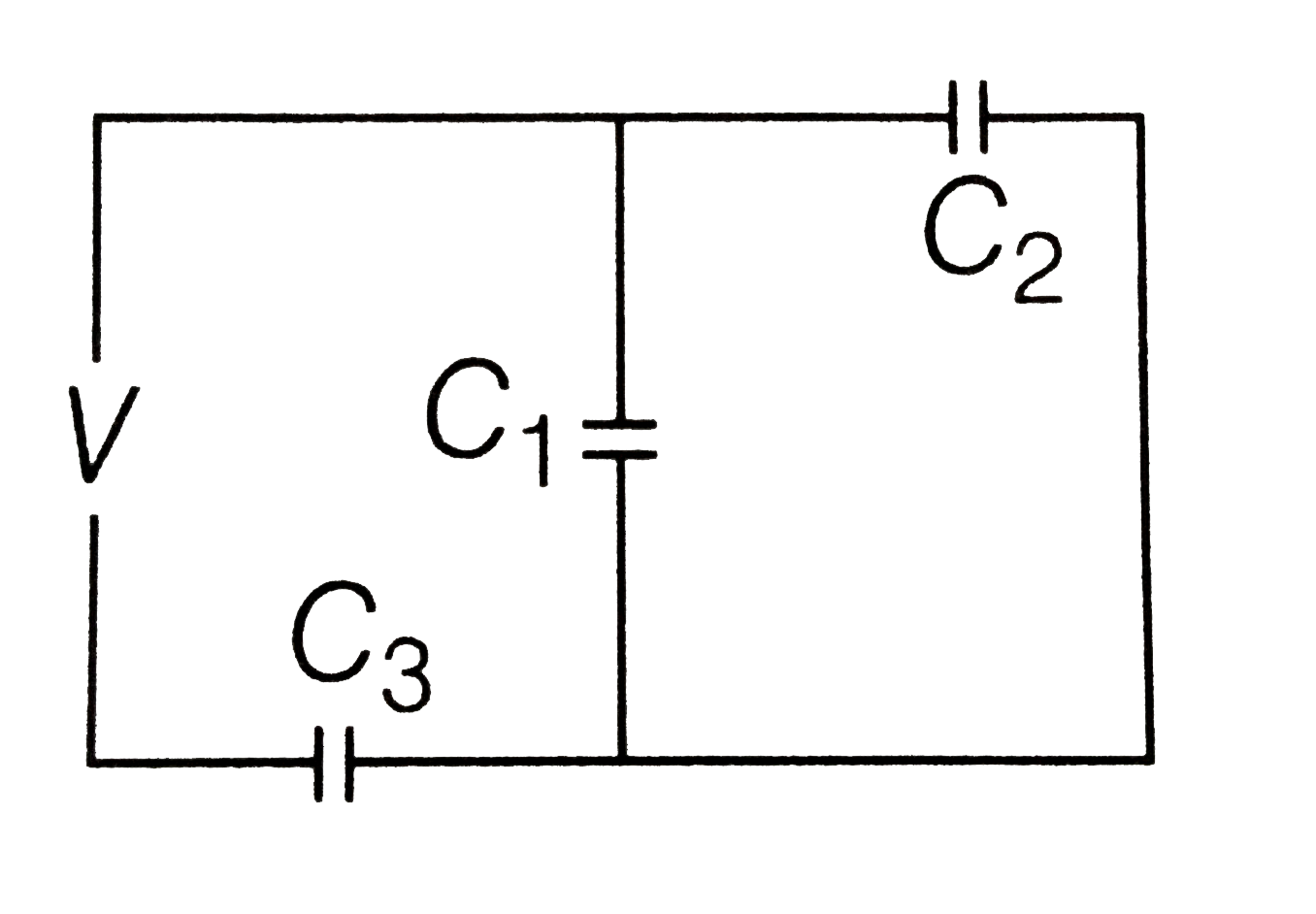
Three capacitors C1=2μF,C26μFandC3=12μFare connected as shown in figure. Find the ratio of the charges on capacitors C1,C2andC3 respectively :
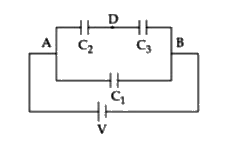
View SolutionThree identical capacitors C1,C2 and C3 of capacitance 6μF each are connected to a 12 V battery as shown in Fig
charge on each capacitor
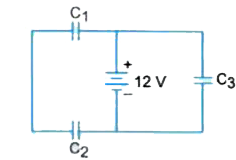
View SolutionThree capacitors C1,C2 and C3 are connected to a battery as shown in the figure . The three capacitors have equal capacitances. Which capacitor stores the most energy ?
View SolutionThree capacitors each of capacitance C=2μF are connected with a battery of emf 30 V as shown in the figure . When the switch S is closed , the heat generated in the circuit will be

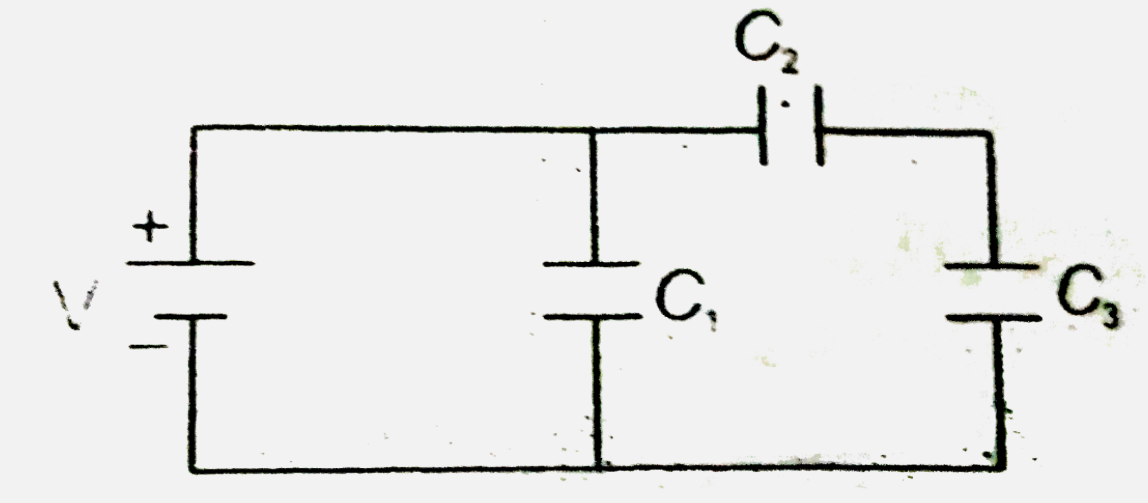
View SolutionThree capacitors C1,C2andC3 are connected as show in the figure to a battery of V volt. If the capacitor C3 breaks down electrically, the change in total charge on the combination of capacitors is
View Solution