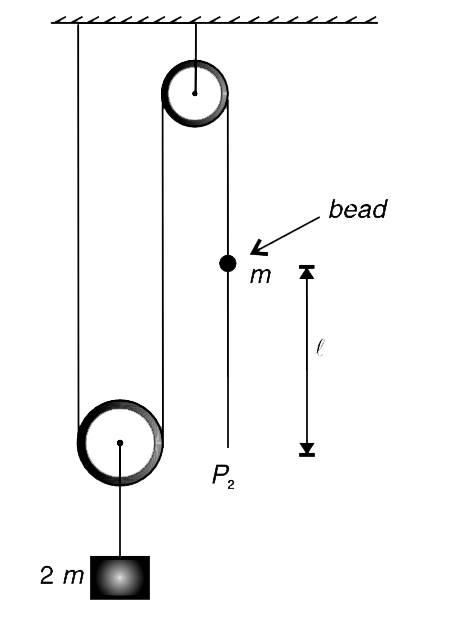
In the system shown in the figure , a bead of mass m can slide on the string. There is friction beween the bead and the string. Block B has mass equal to twice that of the bead. The system is released from rest with lenth l=18.75m of the string hanging below the bead. Assuming the pulley and string to be massless. Find the distance (in meter) moved by the block B before the bead slips out of the thread.

The correct Answer is:0006.25
mg−T=ma1
2mg−2G=2ma2
So, a1=a2
Relative acceleration of bead with respect to end =3a
∴ displacement of block x=12at2=l3=6.25m
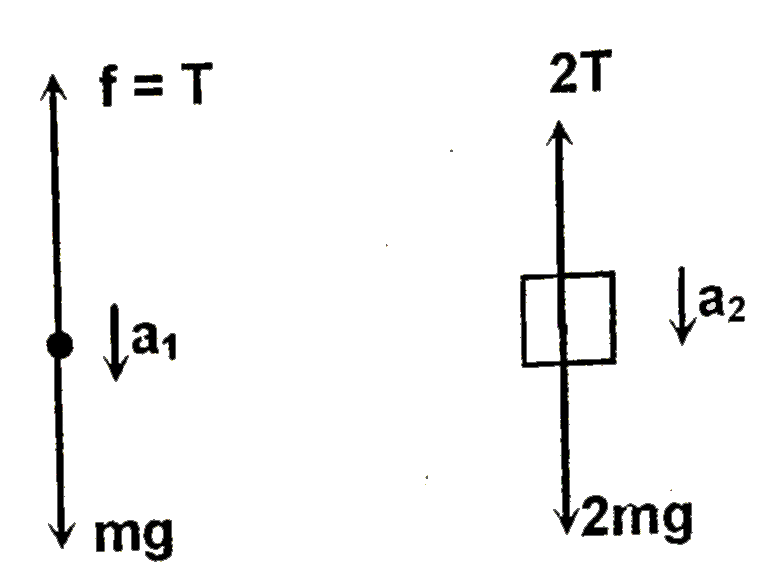
Topper's Solved these Questions
- TEST PAPERSBOOK - FIITJEECHAPTER - TEST PAPERSEXERCISE - PHYSICS
747 Videos
- SIMPLE HARMONIC MOTIONBOOK - FIITJEECHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Assignment Problems (Objective) (Level-II)
20 Videos
- WORK, ENERGY AND POWER BOOK - FIITJEECHAPTER - WORK, ENERGY AND POWER EXERCISE - COMPREHENSIONS ( Comprehension-II)
5 Videos
Similar Questions
In the system shown in the fig., the bead of mass m can slide on the string. There is friction between the bead and the string. Block has mass equal to twice that of the bead. The system is released from rest with length l of the string hanging below the bead. Calculate the distance moved by the block before the bead slips out of the thread. Assume the string and pulley to be massless.
View SolutionIn the system shown in figure, the block A is released from rest. Find
Tension in the string.
View Solution
Knowledge Check
A ring of mass m can slide on the vertical smooth rod. Ring is connected by block with string as shown in figure. Pulley is of mass-less and smooth the system is released from reast. Initial tension in string isAT=MgBT>MgCT<MgDT=Mg+MgIn the system shown all the surfaces are frictionless while pulley and string are massless. The mass of block A is 2m and that of block B is m. The acceleration of block B immediately after system is released from rest is
 Ag/2BgCg/3DNone of these
Ag/2BgCg/3DNone of theseIn the shown mass pulley system, pulleys and string are massless. The one end of the string is pulled by the force F = mg. The acceleration of the block will be :
 Ag/2B0CgD3g
Ag/2B0CgD3g
The system as shown in fig is released from rest. Calculate the tension in the strings and force exerted by the strings on the pulley. Assuming pulleys and strings are massless
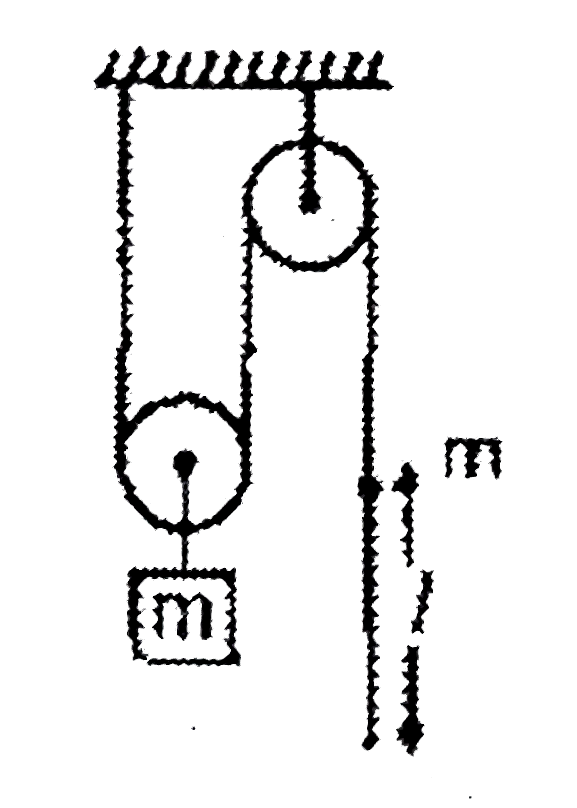
View SolutionIn the figure shown, friction force between the bend and the light string is mg4. Find the time in which the bead loose contact with the string after the system is released from rest.
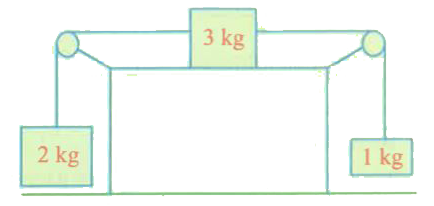
View SolutionThe system shown in fig, is released from rest. Calculate the tension in the string and the force exerted by the string on the pulleys, assuming pulleys and strings are massless.

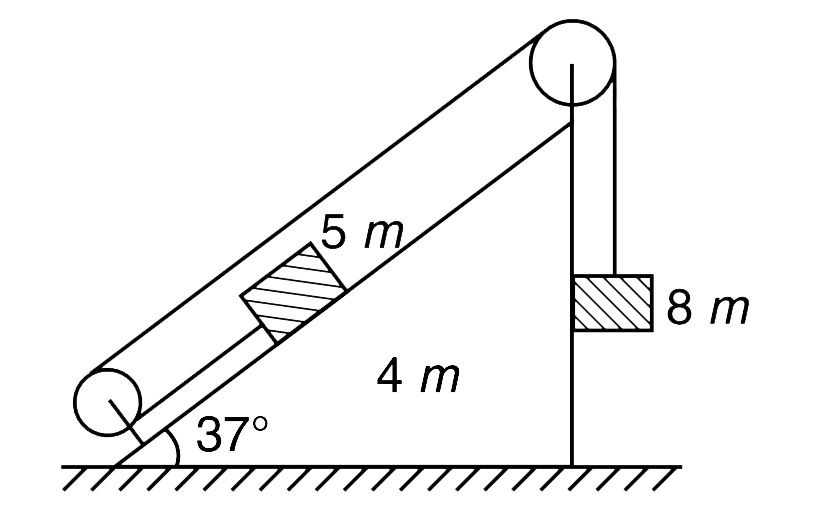
View SolutionIn the system shown in the figure all surfaces are smooth, pulley and string are massless. The string between the two pulleys and between pulley and block of mass 5 m is parallel to the incline surface of the block of mass 4 m. The system is released from rest. Find the acceleration of the block of mass 4 m . [tan37∘=34]
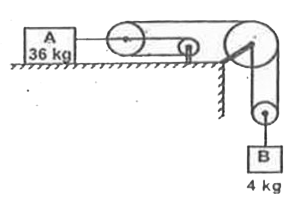
View SolutionIf the system is released from rest, determine the speeds of both masses after B has moved 1 m. Neglect friction, the masses of pulleys and inextensible string.
View Solution
