Two sides of a rhombus OABC ( lying entirely in first quadrant or fourth quadrant) of area equal to 2 sq. units, are y=x√3,y=√3x Then possible coordinates of B is / are ('O' being the origin) Solution in Bengali
(1+√3,1+√3)
(−1−√3,−1−√3)
(3+√3,3+√3)
(√3−1,√3−1)
The correct Answer is:A, B
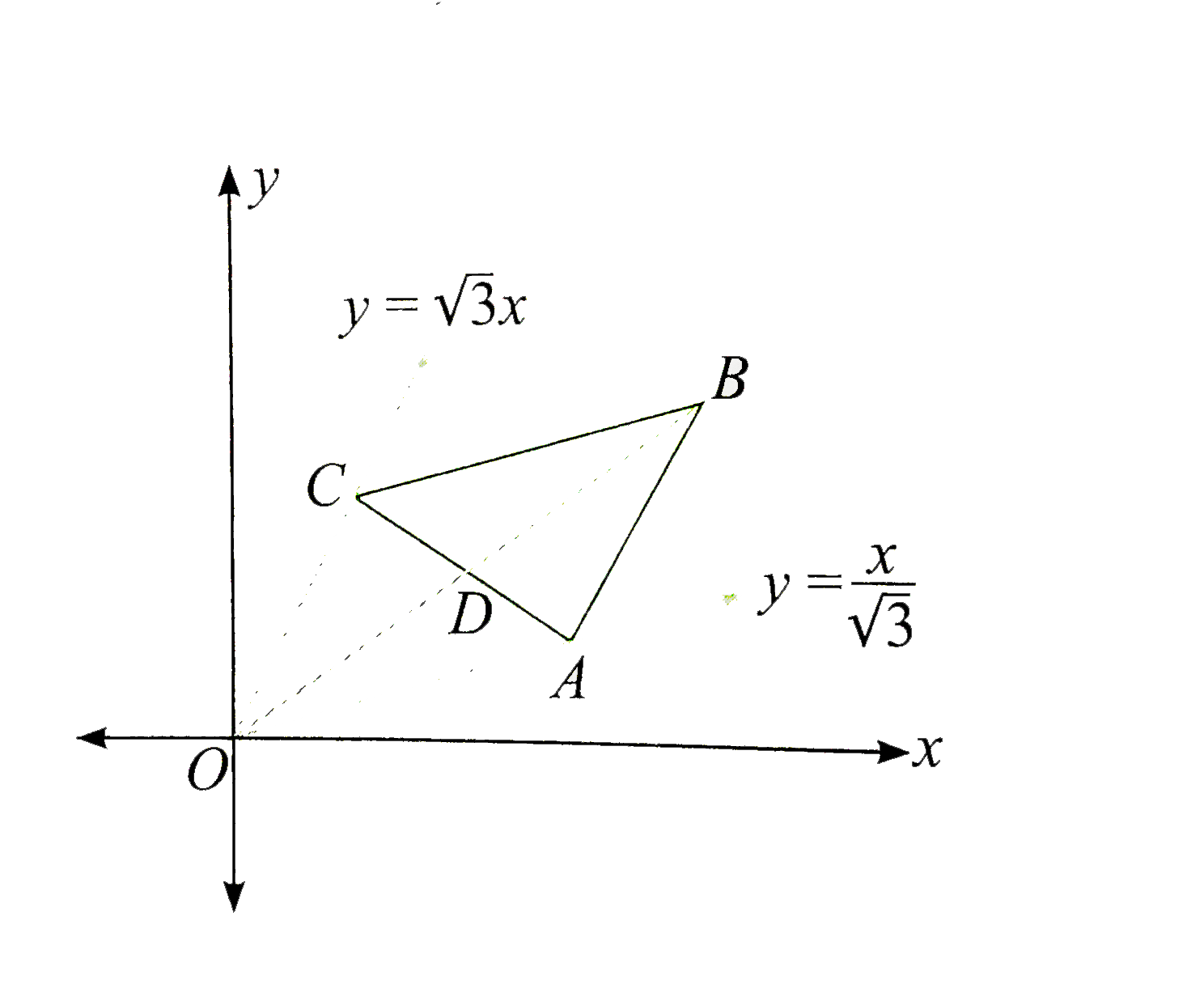
Here,∠COA=30∘.
Area of rhombus =2×12×OA×OCsin30∘
or 2=12x2
or OA = OC =2
Also, ∠OAB=150∘
∴ cos150∘=OA2+AB2−OB22OA×AB
OB2=8+4√3 or OB=√2(√3+1)
Hence, the coordinates of B are (±√2(√3+1) cos 45∘,±√2(√3+1)sin45∘).
Topper's Solved these Questions
- STRAIGHT LINESBook:CENGAGE PUBLICATIONChapter:STRAIGHT LINESExercise:EXERCISE (LINKED COMPREHENSION TYPE)
Explore 27 Videos
- STRAIGHT LINESBook:CENGAGE PUBLICATIONChapter:STRAIGHT LINESExercise:EXERCISE (MATRIX MATCH TYPE)
Explore 8 Videos
- STRAIGHT LINESBook:CENGAGE PUBLICATIONChapter:STRAIGHT LINESExercise:EXERCISE (SINGLE CORRECT ANSWER TYPE)
Explore 82 Videos
- STRAIGHT LINEBook:CENGAGE PUBLICATIONChapter:STRAIGHT LINEExercise:Multiple Correct Answers Type
Explore 8 Videos
- THEORY OF EQUATIONSBook:CENGAGE PUBLICATIONChapter:THEORY OF EQUATIONSExercise:JEE ADVANCED (Numerical Value Type )
Explore 1 Video
Similar Questions
Let l be the line belonging to the family of straight lines (a+2b)x+(a−3b)y+a−8b=0,a,b∈R, which is farthest from the point (2,2), then area enclosed by the line L and the coordinate axes is
View SolutionMatch the following lists:

View SolutionFind the equations of the diagonals of the square formed by the lines x=o,y=0,x=1andy=1.
View SolutionThe point P(α,α+1) will lie inside the triangle whose vertices are A(0,3),B(−2,0) and C(6,1) if
View SolutionThe number of distinct real roots of x4−4x3+12x2+x−1=0is_____.
View SolutionTwo sides of a rhombus OABC ( lying entirely in first quadrant or fourth quadrant) of area equal to 2 sq. units, are y =x/sqrt(3), y=sqrt(3)x Then possible coordinates of B is / are ('O' being the origin)
View SolutionThe area bounded by the curves y=sqrt(x),2y-x+3=0, X-axis and lying in the first quadrant is
View SolutionThe area (in square units) bounded by the curves y=sqrt(x),2y-x+3=0, x-axis, and lying in the first quadrant is
View SolutionArea lying in the first quadrant and bounded by the circle x2+y2=4 the line x=√3y and x-axis , is
View SolutionThe area (in square units) bounded by the curves y=sqrt(x),2y-x+3=0 , x -axis and lying in the first quadrant is -
View SolutionThe area (in sq. units) of the region in the first quadrant bounded by y=x2,y=2x+3 and the y - axis is
View SolutionThe area bounded by the curves y=√x,2y−x+3=0, x-axis and lying in the first quadrant is
View SolutionTwo sides of a rhombus OABC ( lying entirely in first quadrant or fourth quadrant) of area equal to 2 sq. units, are y=x√3,y=√3x Then possible coordinates of B is/are (O being the origin).
View SolutionTwo sides of a rhombus OABC ( lying entirely in first quadrant or fourth quadrant) of area equal to 2 sq. units, are y=x√3,y=√3x Then possible coordinates of B is / are ('O' being the origin)
View SolutionThe area (in square units) bounded by the curves y=sqrt(x),2y-x+3=0, x-axis, and lying in the first quadrant is
View SolutionFind the area bounded by the curve y=√x,x=2y+3 in the first quadrant and Y- axis
View Solution

