If (xa)+(yb)=1 and (xc)+(yd)=1 intersect the axes at four concylic points and a2+c2=b2+d2, then these lines can intersect at, (a,b,c,d>0) Solution in Bengali
(1,1)
(1,-1)
(2,-2)
(3,3)
The correct Answer is:A, B, C and D
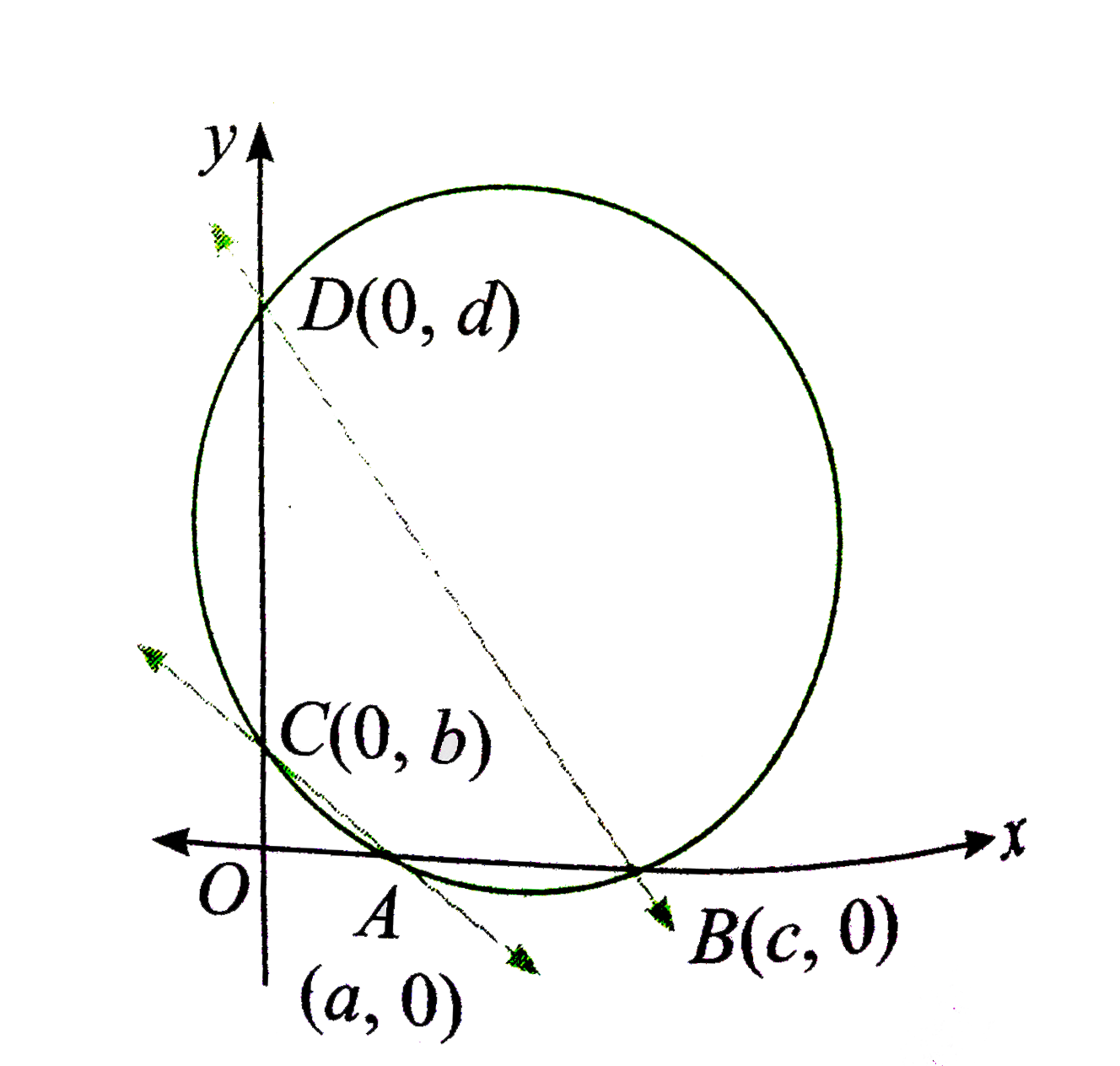
If points A, B,C,D are concyclic, then ac=bd. The coordinates of the points of intersection of lines are
(ac(b−d)bc−ad,bd(c−a)bc−ad)
Let the coordinates of the point of intersection be (h,k). Then
h=ac(b−d)bc−ad,k=bd(c−a)bc−ad
Given c2+a2=b2+d2.Since ac=bd, we have
(c−a)2=(b−d)2
or (c−a)=±(b−d)
Then the locus of the points of intersection is y=±x.
Topper's Solved these Questions
- STRAIGHT LINESBook:CENGAGE PUBLICATIONChapter:STRAIGHT LINESExercise:EXERCISE (LINKED COMPREHENSION TYPE)
Explore 27 Videos
- STRAIGHT LINESBook:CENGAGE PUBLICATIONChapter:STRAIGHT LINESExercise:EXERCISE (MATRIX MATCH TYPE)
Explore 8 Videos
- STRAIGHT LINESBook:CENGAGE PUBLICATIONChapter:STRAIGHT LINESExercise:EXERCISE (SINGLE CORRECT ANSWER TYPE)
Explore 82 Videos
- STRAIGHT LINEBook:CENGAGE PUBLICATIONChapter:STRAIGHT LINEExercise:Multiple Correct Answers Type
Explore 8 Videos
- THEORY OF EQUATIONSBook:CENGAGE PUBLICATIONChapter:THEORY OF EQUATIONSExercise:JEE ADVANCED (Numerical Value Type )
Explore 1 Video
Similar Questions
Let l be the line belonging to the family of straight lines (a+2b)x+(a−3b)y+a−8b=0,a,b∈R, which is farthest from the point (2,2), then area enclosed by the line L and the coordinate axes is
View SolutionMatch the following lists:

View SolutionFind the equations of the diagonals of the square formed by the lines x=o,y=0,x=1andy=1.
View SolutionThe point P(α,α+1) will lie inside the triangle whose vertices are A(0,3),B(−2,0) and C(6,1) if
View SolutionThe number of distinct real roots of x4−4x3+12x2+x−1=0is_____.
View SolutionThe diagonals of a parallelogram ABCD intersect at O. A line through O meets AB in X and CD in Y. Show that ar(AXYD)=12(ARgmABCD)
View SolutionIf (xa)+(yb)=1 and (xc)+(yd)=1 intersect the axes at four concylic points and a2+c2=b2+d2, then these lines can intersect at, (a,b,c,d>0) (1,1) (b) (1,−1) (2,−2) (d) (3,3)
View SolutionIf (x)/(a)+(y)/(b)=1 and (x)/(c)+(y)/(d)=1 intersects the circle at four concyclic points and a^(2)+c^(2)=b^(2)+d^(2). these lines intersects at
View Solution(x-1)(y-2)=5 and (x-1)^(2)+(y+2)^(2)=r^(2) intersect at four points A,B,C,D and if centroid of /_ABC lies on line y=3x-4 then locus of D is
View SolutionThe line x+2y=a intersects the circle x2+y2=4 at two distinct points AandB Another line 12x−6y−41=0 intersects the circle x2+y2−4x−2y+1=0 at two CandD. The value of 'a' for which the points A,B,CandD are concyclic -
View SolutionLine x−y=1 intersect the parabola y2=4x at A and B. Normals at A and B intersect at C. If D is the point at which line CD is normal to the parabola, then coordinate of point D is
View SolutionIf the curves x2a2+y2b2=1andx2c2+y2d2=1 intersect orthogonally, then
View SolutionIf the curves x2a+y2b=1andx2c+y2d=1 intersect at right angles then prove that a−b=c−d
View Solution(x2a)+(y2b)=1 এবং (x2c)+(y2d)=1 বক্ররেখা দুটি পরস্পর লম্বভাবে ছেদ করলে প্রমাণ করো যে,a−b=c−d।
View SolutionIf (xa)+(yb)=1 and (xc)+(yd)=1 intersect the axes at four concylic points and a2+c2=b2+d2, then these lines can intersect at, (a,b,c,d>0) (1,1) (b) (1,−1) (2,−2) (d) (3,3)
View SolutionIf (xa)+(yb)=1 and (xc)+(yd)=1 intersect the axes at four concylic points and a2+c2=b2+d2, then these lines can intersect at, (a,b,c,d>0)
View Solution

