Consider the lines L1≡3x−4y+2=0 and L2≡3y−4x−5=0. Now, choose the correct statement(s).Solution in Bengali
The line x+y=0 bisects the acute angle between L1and L2 containing the origin.
The line x-y+1=0 bisects the obtuse angle between L1 and L2 not containing the origin.
The line x+y+3=0 bisects the obtuse angle between L1 and L2 containing the origin.
The line x-y+1=0 bisects the acute angle between L1 and L2 not containing the origin.
The correct Answer is:A, B
We have L1≡3x−4y+2=0
L2≡4x−3y+5=0
Here, a1a2+b1b2=(3)(4)+(−4)(−3)=24>0
So, acute angle bisector is
3x-4y+2=4x-3y+5
or x+y+3=0
This bisector goes through the regions where expressions 3x-4y+2 and 4x-3y+5 have the same sign.
Also, this is the bisector of anlge which contains origin.
Topper's Solved these Questions
- STRAIGHT LINESBook:CENGAGE PUBLICATIONChapter:STRAIGHT LINESExercise:EXERCISE (LINKED COMPREHENSION TYPE)
Explore 27 Videos
- STRAIGHT LINESBook:CENGAGE PUBLICATIONChapter:STRAIGHT LINESExercise:EXERCISE (MATRIX MATCH TYPE)
Explore 8 Videos
- STRAIGHT LINESBook:CENGAGE PUBLICATIONChapter:STRAIGHT LINESExercise:EXERCISE (SINGLE CORRECT ANSWER TYPE)
Explore 82 Videos
- STRAIGHT LINEBook:CENGAGE PUBLICATIONChapter:STRAIGHT LINEExercise:Multiple Correct Answers Type
Explore 8 Videos
- THEORY OF EQUATIONSBook:CENGAGE PUBLICATIONChapter:THEORY OF EQUATIONSExercise:JEE ADVANCED (Numerical Value Type )
Explore 1 Video
Similar Questions
Let l be the line belonging to the family of straight lines (a+2b)x+(a−3b)y+a−8b=0,a,b∈R, which is farthest from the point (2,2), then area enclosed by the line L and the coordinate axes is
View SolutionMatch the following lists:

View SolutionFind the equations of the diagonals of the square formed by the lines x=o,y=0,x=1andy=1.
View SolutionThe point P(α,α+1) will lie inside the triangle whose vertices are A(0,3),B(−2,0) and C(6,1) if
View SolutionThe number of distinct real roots of x4−4x3+12x2+x−1=0is_____.
View SolutionL_(1)=x+3y-5=0,L_(2)=3x-ky-1=0,L_(3)=5x+2y-12=0 are concurrent if k=
View SolutionConsider the lines L1≡3x−4y+2=0 and L2≡3y−4x−5=0. Now, choose the correct statement(s).
View SolutionConsider the lines given by L_(1):x+3y-5=0 L_(2):3x-ky-1=0 L_(3):5x+2y-12=0 Match the following lists.
View SolutionConsider four straight lines
(i)l1=3y=4x+5 (ii)l2:4y=3x−1
(iii)l3:4y+3y=7 (iv)l44x+3y=2
View SolutionConsider the lines given by
L1:x+3y−5=0, L2:3x−ky−1=0 L3:5x+2y−12=0
Column-IColumn-II(A),L1,L2,L3 are concurrent, if(p)k=−9(B) One of L1,L2,L3 is parallel to at least one of the other two, if(q)k=−65(C)L1,L2,L3 from a triangle, if(r)k=56(D)L1,L2,L3 do not from a triangle, if(s)k=5
View SolutionShow that two pairs of lines 3x2+8xy−3y2=0and3x2+8xy−3y2+2x−4y−1=0 forms a square.
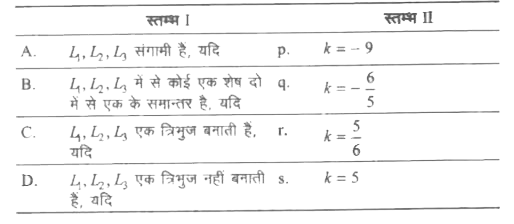
View Solutionमाना रेखाओं के समीकरण
L1:x+3y−5=0,L2:3x−ky−1=0
तथा L3:5x+2y−12=0 हैं।
स्तम्भ I में कथन/व्यंजक को स्तम्भ II के कथन/ व्यंजक से सुमेल कीजिए।
View Solutionl1:3y=4x+5, l2:4y=3x−1, l3:4y+3x=7, l4:4x+3y=2 எனக் கொடுக்கப்பட்ட நான்கு நேர்கோடுகளுக்குக் கீழக்கண்ட கூற்றுகளில் எது உண்மை ?
View SolutionConsider the lines L1≡3x−4y+2=0 and L2≡3y−4x−5=0. Now, choose the correct statement(s).
(a)The line x+y=0 bisects the acute angle between L1and L2 containing the origin.
(b)The line x-y+1=0 bisects the obtuse angle between L1 and L2 not containing the origin.
(c)The line x+y+3=0 bisects the obtuse angle between L1 and L2 containing the origin.
(d)The line x-y+1=0 bisects the acute angle between L1 and L2 not containing the origin.
View SolutionConsider the lines given by L_(1):x+3y-5=0 L_(2):3x-ky-1=0 L_(3):5x+2y-12=0 Match the following lists.
View Solution

