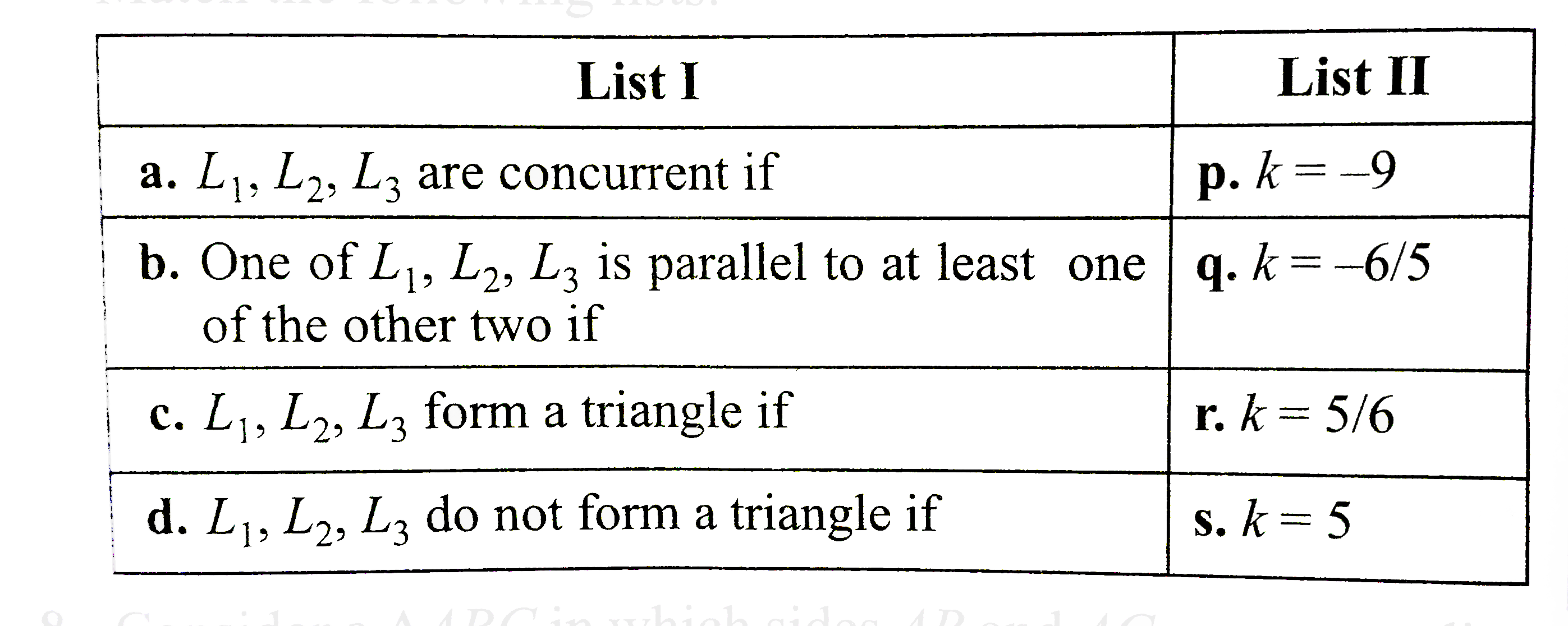The three lines l1=4x−3y+2=0,l2=3x+4y−4=0 and l3=x−7y+6=0
form a rt. angled isosceles triangle
form a rt. Angled triangle
are concurrent
None
The correct Answer is:C
To determine whether the three lines l1=4x−3y+2=0, l2=3x+4y−4=0, and l3=x−7y+6=0 are concurrent or not, we can use the determinant method. If the determinant is equal to zero, then the lines are concurrent; otherwise, they are not.
1. Identify the coefficients of the lines:
- For line l1:4x−3y+2=0 → a1=4,b1=−3,c1=2
- For line l2:3x+4y−4=0 → a2=3,b2=4,c2=−4
- For line l3:x−7y+6=0 → a3=1,b3=−7,c3=6
2. Set up the determinant:
The determinant Δ is given by:
Δ=∣∣
∣∣a1b1c1a2b2c2a3b3c3∣∣
∣∣=∣∣
∣∣4−3234−41−76∣∣
∣∣
3. Calculate the determinant:
We can expand the determinant using the first row:
Δ=4∣∣∣4−4−76∣∣∣−(−3)∣∣∣3−416∣∣∣+2∣∣∣341−7∣∣∣
Now calculating each of the 2x2 determinants:
- ∣∣∣4−4−76∣∣∣=(4)(6)−(−4)(−7)=24−28=−4
- ∣∣∣3−416∣∣∣=(3)(6)−(−4)(1)=18+4=22
- ∣∣∣341−7∣∣∣=(3)(−7)−(4)(1)=−21−4=−25
Substituting back into the determinant:
Δ=4(−4)+3(22)+2(−25)=−16+66−50=0
4. Conclusion:
Since Δ=0, the lines are concurrent and do not form a triangle.
Final Answer:
The lines are concurrent and do not form a triangle.
---
- For line l1:4x−3y+2=0 → a1=4,b1=−3,c1=2
- For line l2:3x+4y−4=0 → a2=3,b2=4,c2=−4
- For line l3:x−7y+6=0 → a3=1,b3=−7,c3=6
The determinant Δ is given by:
Δ=∣∣
∣∣a1b1c1a2b2c2a3b3c3∣∣
∣∣=∣∣
∣∣4−3234−41−76∣∣
∣∣
We can expand the determinant using the first row:
Δ=4∣∣∣4−4−76∣∣∣−(−3)∣∣∣3−416∣∣∣+2∣∣∣341−7∣∣∣
- ∣∣∣4−4−76∣∣∣=(4)(6)−(−4)(−7)=24−28=−4
- ∣∣∣3−416∣∣∣=(3)(6)−(−4)(1)=18+4=22
- ∣∣∣341−7∣∣∣=(3)(−7)−(4)(1)=−21−4=−25
Δ=4(−4)+3(22)+2(−25)=−16+66−50=0
Since Δ=0, the lines are concurrent and do not form a triangle.
The lines are concurrent and do not form a triangle.
Topper's Solved these Questions
- RECTANGULAR CARTESIAN CO-ORDINATE SYSTEM AND THE STRAIGHT LINEBook:ML KHANNAChapter:RECTANGULAR CARTESIAN CO-ORDINATE SYSTEM AND THE STRAIGHT LINEExercise:PROBLEM SET(2)(TRUE AND FALSE)
Explore 7 Videos
- RECTANGULAR CARTESIAN CO-ORDINATE SYSTEM AND THE STRAIGHT LINEBook:ML KHANNAChapter:RECTANGULAR CARTESIAN CO-ORDINATE SYSTEM AND THE STRAIGHT LINEExercise:PROBLEM SET(2)(fill in the blanks)
Explore 2 Videos
- RECTANGULAR CARTESIAN CO-ORDINATE SYSTEM AND THE STRAIGHT LINEBook:ML KHANNAChapter:RECTANGULAR CARTESIAN CO-ORDINATE SYSTEM AND THE STRAIGHT LINEExercise:PROBLEM SET(1)(FILL IN THE BLANK)
Explore 3 Videos
- PROPERTIES OF TRIANGLES Book:ML KHANNAChapter:PROPERTIES OF TRIANGLES Exercise:Self Assessment Test (Multiple Choise Questions)
Explore 34 Videos
- SELF ASSESSMENT TEST Book:ML KHANNAChapter:SELF ASSESSMENT TEST Exercise:OBJECTIVE MATHEMATICS
Explore 16 Videos
Similar Questions
Knowledge Check
The three lines 4x +4y = 1 , 8 x - 3y = 2 , y = 0 are
AThe sides of an isosceles triangleBConcurrentCMutually perpendicularDThe sides of an equilateral triangleConsider the lines L1≡3x−4y+2=0 and L2≡3y−4x−5=0. Now, choose the correct statement(s).
AThe line x+y=0 bisects the acute angle between L1and L2 containing the origin.BThe line x-y+1=0 bisects the obtuse angle between L1 and L2 not containing the origin.CThe line x+y+3=0 bisects the obtuse angle between L1 and L2 containing the origin.DThe line x-y+1=0 bisects the acute angle between L1 and L2 not containing the origin.Three lines 3x+4y+6=0,√2x+√3y+2√2=0and4x+7y+8=0 are (A) sides of triangle (B) concurrent (C) parallel (D) none of these
Asides of a triangleBconcurrent at (1,1)CparallelDNone of these
Consider the lines give by L1:x+3y−5=0,L2:3x−ky−1=0,L3:5x+2y−12=0

View SolutionConsider the lines given by
L1=x+3y–5=0
L2=3x–ky–1=0
L3=5x+2y–12=0
Match the statements/Expression in Column-I with the statements/Expressions in Column-II and indicate your answer by darkening the appropriate bubbles in the 4 × 4 matrix given in OMR.

View SolutionConsider the lines given by
L1:x+3y−5=0, L2:3x−ky−1=0 L3:5x+2y−12=0
Column-IColumn-II(A),L1,L2,L3 are concurrent, if(p)k=−9(B) One of L1,L2,L3 is parallel to at least one of the other two, if(q)k=−65(C)L1,L2,L3 from a triangle, if(r)k=56(D)L1,L2,L3 do not from a triangle, if(s)k=5
View SolutionIf the lines L1:x−2y+4z=0,2x+y+z−4=0 and L2:x−22=y1=z−12a are perpendicular, then a is equal to
View SolutionConsider the lines give by L1:x+3y−5=0,L2:3x−ky−1=0,L3:5x+2y−12=0

View Solution