The area (in square units) bounded by the curves y=√x,2y−x+3=0, x-axis, and lying in the first quadrant is
A
9
B
36
C
18
D
274
Video Solution
Text Solution
The correct Answer is:A
y=√xand2y−x+3=0
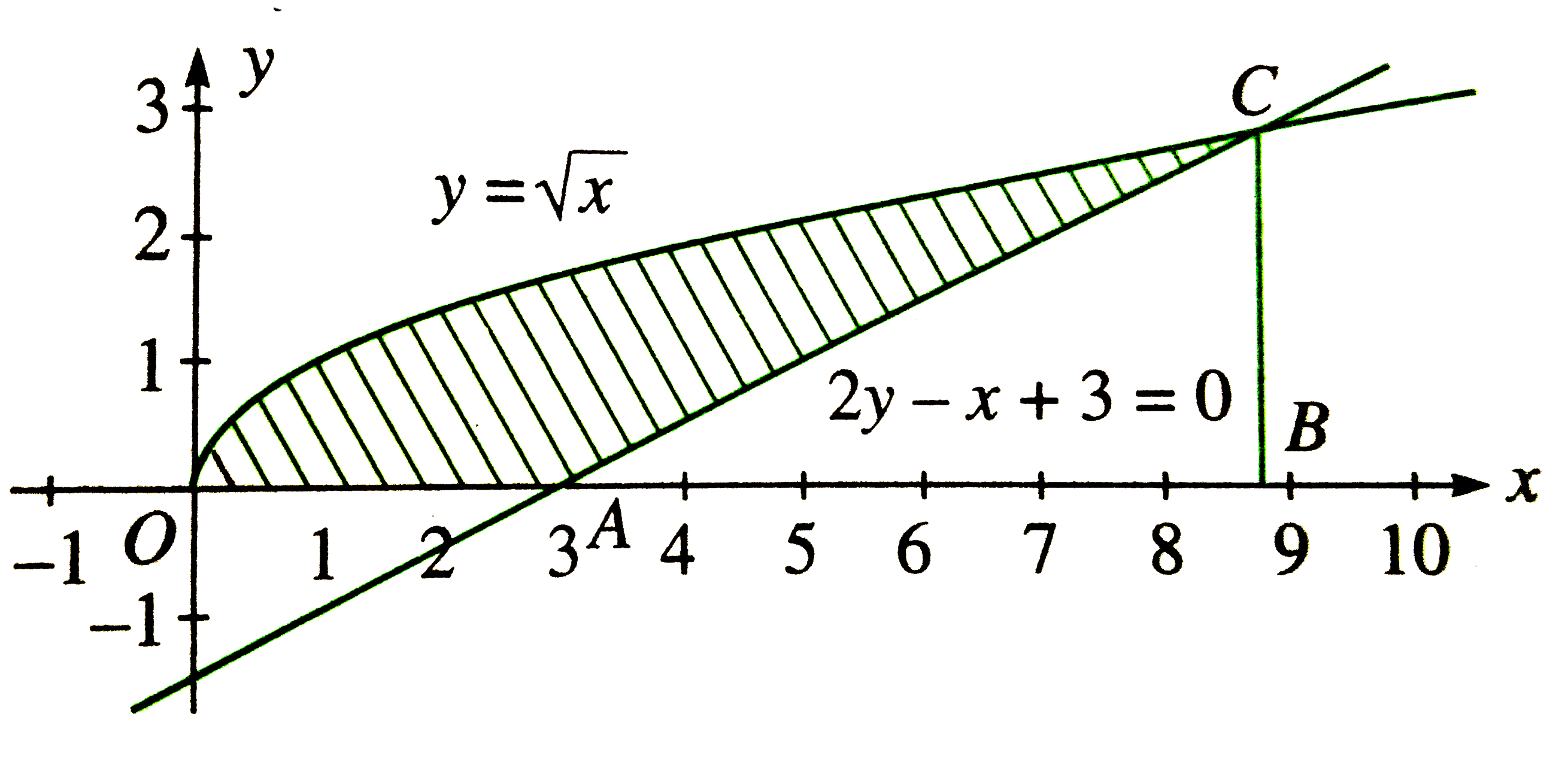
∴ Required area = Area of region OABCO-Area of ΔABC
=9∫0√xdx−12×BC×AB
=(x3/23/2)90−12×3×6
=9 sq. units
|
Topper's Solved these Questions
- AREABOOK - CENGAGECHAPTER - AREAEXERCISE - JEE Advanced Previous Year
9 Videos
- AREABOOK - CENGAGECHAPTER - AREAEXERCISE - Multiple Correct Answer Type
3 Videos
- AREABOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise (Numerical)
16 Videos
- APPLICATIONS OF DERIVATIVESBOOK - CENGAGECHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Question Bank
29 Videos
- AREA UNDER CURVESBOOK - CENGAGECHAPTER - AREA UNDER CURVESEXERCISE - Question Bank
20 Videos
Similar Questions
Knowledge Check
The area (in square units) bounded by the curves y=√x,2y−x+3=0, x-axis, and lying in the first quadrant is
A9B36C18D274The area bounded by the curves x+y=2 and y=x2 above x-axis in the first quadrant is ,
A12B23C1012D65The area (in sq. units) of the region bounded by the curves y=2x and y=|x+1|, in the first quadrant is :
A32−1loge2Bloge2+32C32D12
Find the area of the region bounded by the curve y=√36−x2, the X- axis lying in the first quadrant and the lines X= 0, X = 6 ?
View SolutionThe area (in square units) bounded by the curve y=x3, the x-axis and the ordinates at x=−2andx=1 is
View SolutionFind the area of the region bounded by the curve x=√25−y2, the Y- axis lying in the first quadrant and the lines y=0andy=5.
View SolutionArea (in square units) of the region bounded by the curve y2=4x,y-axis and the line y=3 , is
View SolutionThe area in square units bounded by the curves y=x3,y=x2 and the ordinates x=1,x=2 is
View Solution
