The area of the region bounded by the parabola (y2)2=x1 , the tangent to the parabola at the point (2, 3) and the xaxis is (1) 3 (2) 6 (3) 9 (4) 12

A

3

B

6

C

9

D

12

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:C

The given parabola is (y−2)2=x−1. So
dydx=12(y−2)
At(2,3),
dydx=12(3−2)=12
Tangent at (2,3) is
y−3=12(x−2)⇒x−2y+4=0
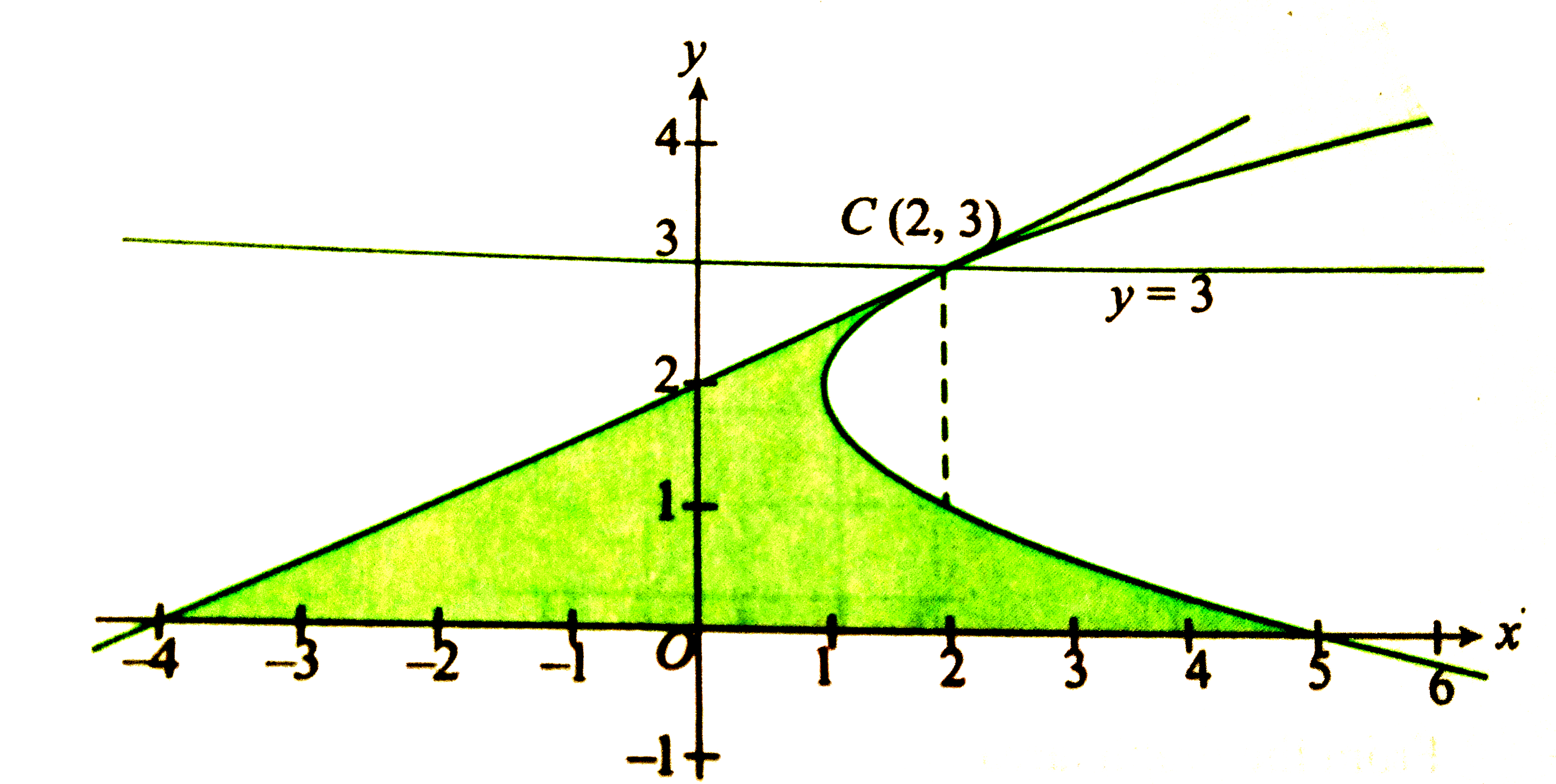
ocr_image
Therefore, the required area
=3∫0[(y−2)2+1]dy−3∫0(2y−4)dy
=∣∣ ∣∣(y−2)33+y∣∣ ∣∣30−∣∣y2−4y∣∣30
=13+3+83−(9−12)
=9 sq. units

Updated on:21/07/2023
|
Class 12MATHSAPPLICATION OF INTEGRALS

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • The area of the region bounded by the parabola (y−2)2=x−1, the tangent to the parabola at the point (2,3) and the x-axis is

    A7 sq. units
    B6 sq. units
    C9 sq. units
    DNone of these

  • The area of the region bounded by the parabola (y−2)2=x−1, the tangent to the parabola at the point (2,3) and the x-axis is

    A7 sq. units
    B6 sq. units
    C9 sq. units
    DNone of these

  • The area of the region bounded by the parabola (y−2)2=x−1, the tangent to the parabola at the point (2,3) and the X-axis is

    A7 sq. units
    B6 sq. units
    C9 sq. units
    DNone of these