The area (in square units) bounded by the curves x-axis, and lying in the first quadrant isSolution in Tamil
9
36
18
The correct Answer is:A
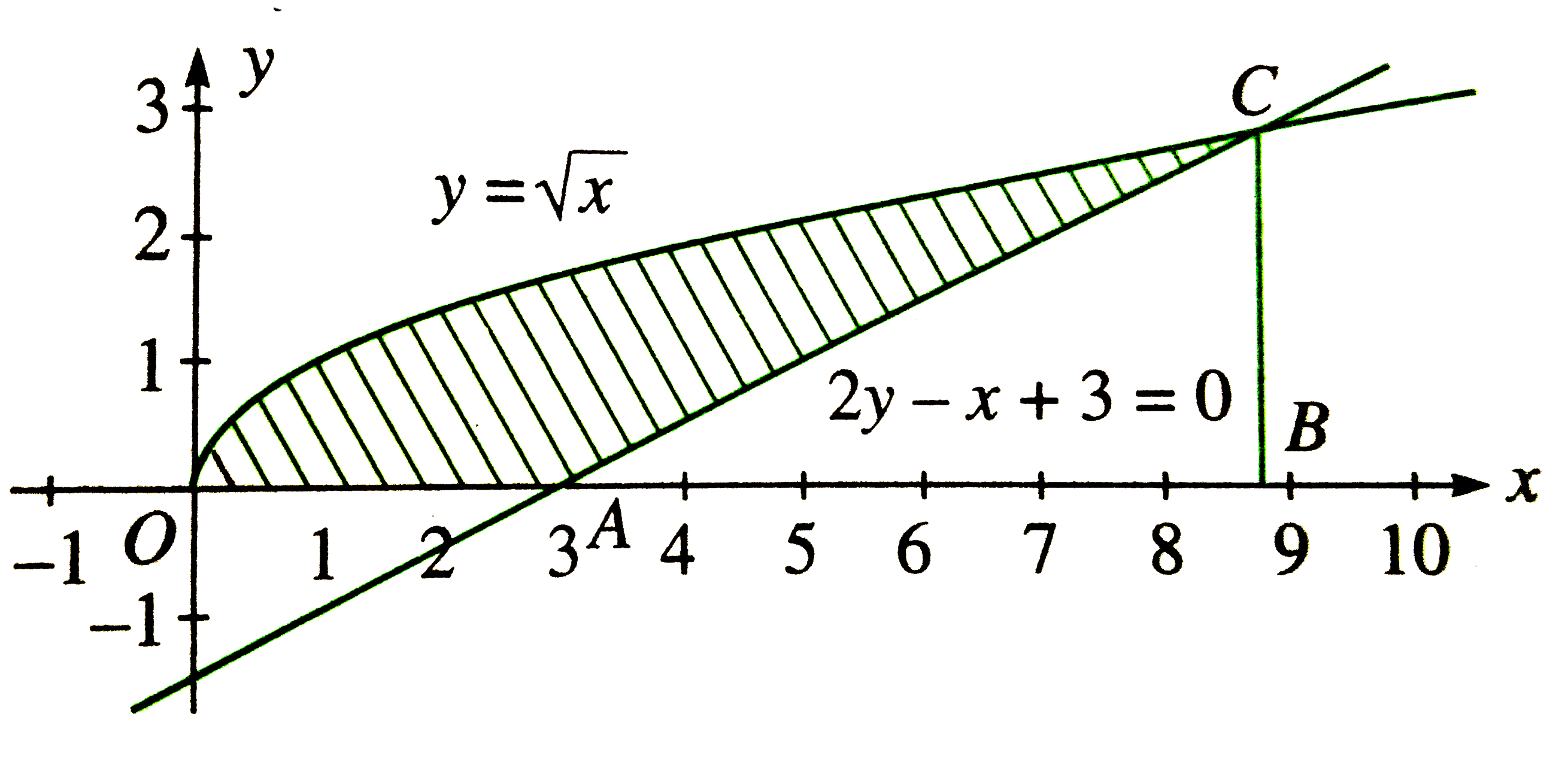
Required area = Area of region OABCO-Area of
sq. units
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - AREAEXERCISE - JEE Advanced Previous Year9videos
AREA
- BOOK - CENGAGECHAPTER - AREAEXERCISE - Single Correct Answer Type27videos
AREA
- BOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise (Numerical)16videos
AREA
- BOOK - CENGAGECHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Subjective Type2videos
APPLICATIONS OF DERIVATIVES
- BOOK - CENGAGECHAPTER - AREA UNDER CURVESEXERCISE - Question Bank10videos
AREA UNDER CURVES
Similar Questions
Find the area bounded by the curves x+2|y|=1 and x=0.
03:59View SolutionThe area enclosed between the curve y=sin2xandy=cos2x in the interval 0≤x≤π is _____ sq. units.
05:26View SolutionThe area enclosed by the curve C:y=x√9−x2(x≥0) and the x-axis is___.
03:29View SolutionProve that for λ>1, the equation xlogx+x=λ has least one solution in [1,λ].
04:23View SolutionThe area of the region (s) enclosed by the curves y=x2 and y=√|x| is
05:31View SolutionThe area bounded by the curves y=sqrt(x),2y-x+3=0, X-axis and lying in the first quadrant is
07:22View SolutionFind the area lying in the first quadrant, bounded by the curves y2−x+2=0 and y=|x−2|.
06:09View SolutionFind the area bounded by the curve y=√x,x=2y+3 in the first quadrant and X-axis.
02:28View SolutionFind the area bounded by the curve y=√x,x=2y+3 in the first quadrant and X-axis.
06:08View Solutionवक्रो y=√x,2y−x+3=0 तथा x अक्ष से घिरे उस क्षेत्र का क्षेत्रफल ज्ञात कीजिए जो प्रथम चतुर्थांश में स्थित है |
05:11View Solutionसिद्ध कीजिए की वक्रों y=√x,2y+3=x तथा x अक्ष से सीमाबद्ध (प्रथम पाद में) क्षेत्र का क्षेत्रफल 9 इकाई होगा|
02:47View SolutionArea ( in square unit ) bounded by the curve y=√x , the straight line x=2y+3 in first quadrant and x- axis is-
05:55View SolutionArea bounded by the curves : y=√x,x=2y+3 in the first quadrant and x-axis is :
09:32View SolutionThe area bounded by the curves y=√x,2y−x+3=0, x-axis and lying in the first quadrant is
05:18View SolutionFind the area bounded by the curve y=√x,x=2y+3 in the first quadrant and X-axis.
07:54View Solutiony^(2) =16 -x^2 And y = 0 is the area (in square units) of the area bounded by x = 0 in the first quadrant.
02:28View Solution
