A bullet is fired from horizontal ground at some angle passes through the point (3R/4 ,R/4), where R is the range of the bullet. Assume point of the fire to be origin and the bullet moves in x-y plane with x-axis horizontal and y-axis vertically upwards. Then angle of projection is
30∘
37∘
53∘
none
The correct Answer is:C
To solve the problem, we need to find the angle of projection of a bullet fired from the horizontal ground that passes through the point (3R4,R4), where R is the range of the bullet.
1. Understanding the Projectile Motion:
The bullet follows a parabolic trajectory. The horizontal and vertical motions can be described using the equations of projectile motion. The horizontal range R is given by:
R=u2sin2θg
where u is the initial velocity, θ is the angle of projection, and g is the acceleration due to gravity.
2. Equation of Trajectory:
The equation of the trajectory of the projectile is given by:
y=xtanθ−gx22u2cos2θ
We will use this equation to find the angle θ.
3. Substituting the Given Point:
We know the bullet passes through the point (3R4,R4). We will substitute x=3R4 and y=R4 into the trajectory equation:
R4=3R4tanθ−g(3R4)22u2cos2θ
4. Simplifying the Equation:
Rearranging the equation gives:
R4+g(3R4)22u2cos2θ=3R4tanθ
Dividing through by R (assuming R≠0):
14+g(34)22u2cos2θ=34tanθ
5. Using the Range Formula:
From the range formula, we can express u2 in terms of R and θ:
u2=gRsin2θ
Substituting this into our equation gives:
14+g(34)22(gRsin2θ)cos2θ=34tanθ
6. Further Simplifying:
Simplifying the left-hand side:
14+9g162gRsin2θcos2θ=34tanθ
This simplifies to:
14+9sin2θ32Rcos2θ=34tanθ
7. Finding tanθ:
Rearranging gives:
9sin2θ32Rcos2θ=34tanθ−14
Solving this equation will yield tanθ.
8. Final Calculation:
After solving, we find:
tanθ=43
Thus, the angle of projection θ can be calculated as:
θ=tan−1(43)
This gives approximately:
θ≈53∘
Final Answer:
The angle of projection is 53∘.
The bullet follows a parabolic trajectory. The horizontal and vertical motions can be described using the equations of projectile motion. The horizontal range R is given by:
R=u2sin2θg
where u is the initial velocity, θ is the angle of projection, and g is the acceleration due to gravity.
The equation of the trajectory of the projectile is given by:
y=xtanθ−gx22u2cos2θ
We will use this equation to find the angle θ.
We know the bullet passes through the point (3R4,R4). We will substitute x=3R4 and y=R4 into the trajectory equation:
R4=3R4tanθ−g(3R4)22u2cos2θ
Rearranging the equation gives:
R4+g(3R4)22u2cos2θ=3R4tanθ
Dividing through by R (assuming R≠0):
14+g(34)22u2cos2θ=34tanθ
From the range formula, we can express u2 in terms of R and θ:
u2=gRsin2θ
Substituting this into our equation gives:
14+g(34)22(gRsin2θ)cos2θ=34tanθ
Simplifying the left-hand side:
14+9g162gRsin2θcos2θ=34tanθ
This simplifies to:
14+9sin2θ32Rcos2θ=34tanθ
Rearranging gives:
9sin2θ32Rcos2θ=34tanθ−14
Solving this equation will yield tanθ.
After solving, we find:
tanθ=43
Thus, the angle of projection θ can be calculated as:
θ=tan−1(43)
This gives approximately:
θ≈53∘
The angle of projection is 53∘.
Topper's Solved these Questions
- CENGAGE PHYSICS DPPBook:CENGAGE PHYSICS ENGLISHChapter:CENGAGE PHYSICS DPPExercise:subjective type
Explore 51 Videos
- CENGAGE PHYSICS DPPBook:CENGAGE PHYSICS ENGLISHChapter:CENGAGE PHYSICS DPPExercise:Multiple correct Answer Type
Explore 54 Videos
- CAPACITOR AND CAPACITANCEBook:CENGAGE PHYSICS ENGLISHChapter:CAPACITOR AND CAPACITANCEExercise:Integer
Explore 5 Videos
- COULOMB LAW AND ELECTRIC FIELDBook:CENGAGE PHYSICS ENGLISHChapter:COULOMB LAW AND ELECTRIC FIELDExercise:Single Answer Correct Type
Explore 22 Videos
Similar Questions
A particle is projected from gound At a height of 0.4 m from the ground, the velocity of a projective in vector form is →v=(6ˆi+2ˆj)m/s (the x-axis is horizontal and y-axis is vertically upwards). The angle of projection is (g=10m/s2)
View SolutionA plane passes through thee points P(4,0,0)andQ(0,0,4) and is parallel to the Y-axis. The distance of the plane from the origin is
View Solution
Knowledge Check
The point on the curve y2=x , where tangent make an angle of π4 with the x-axis, is
A(12,14)B(14,12)C(4,2)D(1,1)
Write the coordinates of the point on the curve y2=x where the tangent line makes an angle π4 with x-axis.
View SolutionTwo graphs of the same projectile motion (in the xy-plane) projected from origin are shown. X-axis is along horizontal direction and y-axis is vertically upwards. Take g=10ms−2.
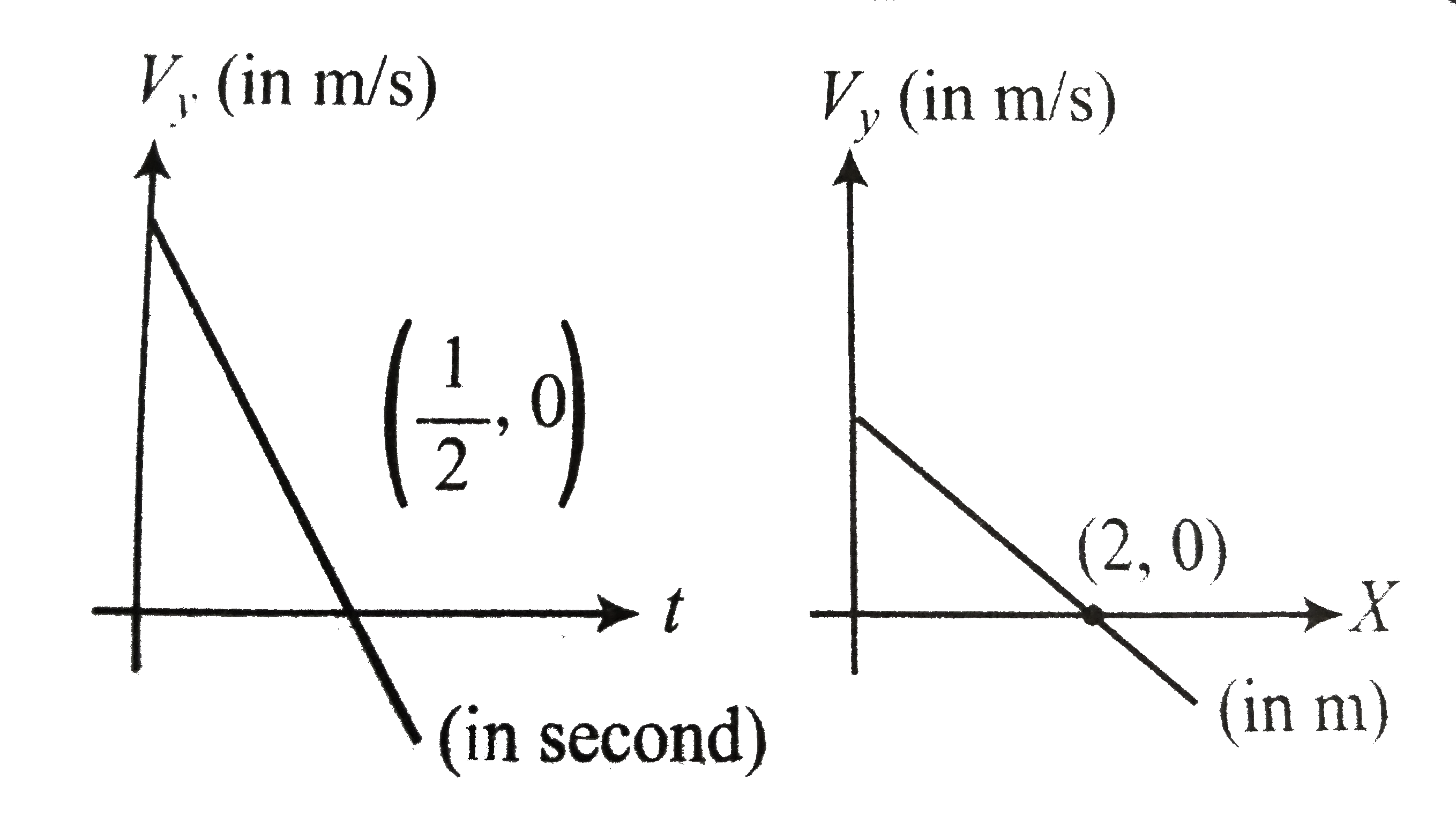 ,
,
The projection speed is :
View SolutionIf the time of flight of a bullet over a horizontal range R is T, then the angle of projection with horizontal is -
View SolutionFind the equation of the plane passes through the point (2,3,−4) and (1,−1,3) and parallel to x-axis.
View SolutionThe graph of a line in the xy-plane passes through the point (1, 4) and crosses the x-axis at the point (2, 0). The line crosses the y-axis at the point (0, b). What is the value of b ?
View SolutionThe equation of the parabola whose vertex is origin axis along x-axis and which passes through the point (-2,4) is
View SolutionA horizontal plane 4x−3y+7z=0 is given. Find a line of greatest slope passes through the point (2,1,1) in the plane 2x+y−5z=0.
View Solution