
A particle is projected from point A on plane AB, so that AB=2u2tanθg√3 in the figure as shown. If u is the velocity of projection, find angle θ.
30∘
60∘
90∘
45∘
The correct Answer is:A
Time of flight t=2usin(2θ−θ)gcosθ=2ugtanθ
AB=2u2tanθg√3=u√3t ..(i)
uH=ucos2θ
AC=uH.t=ucos2θt
AB=ACcosθ=ucos2θtcosθ …(ii)
Compare equations (i) and (ii)
cos2θcosθ=1√3 or θ=30∘
Similar Questions
A particle is projected at an angle θ with an initial speed u.
View SolutionA particle is projected horizontally with a speed u from the top of plane inclined at an angle θ with the horizontal. How far from the point of projection will the particle strike the plane ?

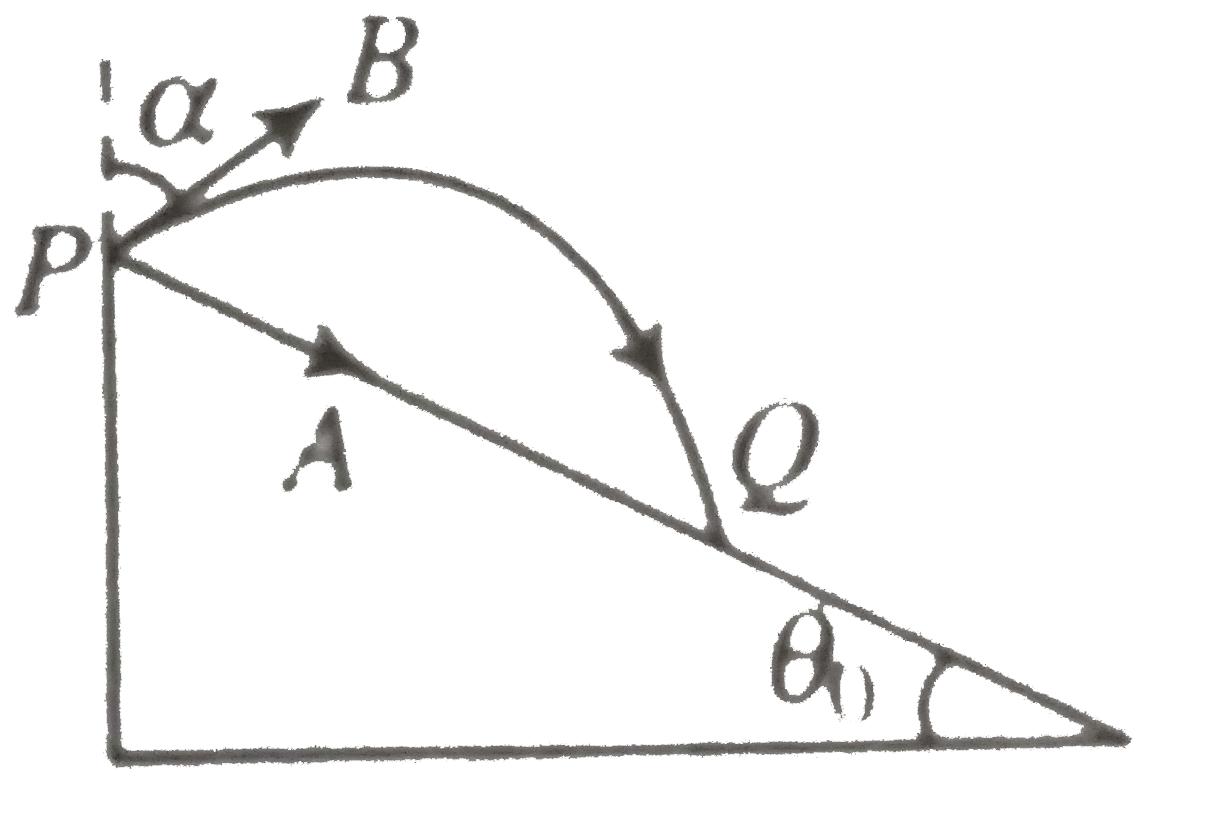
View SolutionFigure shows that particle A is projected from point P with velocity u along the plane and simultaneously another particle B with velocity v at an angle α with vertical. The particles collide at point Q on the plane. Then
View SolutionA particle is projected from a point on the level ground and its height is h when at horizontal distances aand2a from its point of projection. Find the velocity of projection.
View SolutionA particle is projected at an angle of elevation α and after t second it appears to have an elevation of β as seen from the point of projection. Find the initial velocity of projection.
View SolutionWhat is the radius of curvature of the parabola traced out by the projectile in which a particle is projected with a speed u at an angle θ with the horizontal, at a point where the velocity of particle makes an angle θ/2 with the horizontal.
View SolutionA particle is projected from a point A with velocity √2u an angle of 45∘ with horizontal as shown in figure. It strikes the plane BC at right angles. The velocity of the particle at the time of collision is

View SolutionA particle is projected with speed u at angle θ to the horizontal. Find the radius of curvature at highest point of its trajectory
View SolutionA particle is projected from ground at an angle θ with horizontal with speed u. The ratio of radius of curvature of its trajectory at point of projection to radius of curvature at maximum height is -
View SolutionA ball is projected perpendicularly from an inclined plane of angle θ, with speed 'u' as shown. The time after which the projectile is making angle 45∘ with the inclined plane is :

View Solution