
A particle is projected from surface of the inclined plane with speed u and at an angle θ with the horizontal. After some time the particle collides elastically with the smooth fixed inclined plane for the first time and subsequently moves in vertical direction. Starting from projection, find the time taken by the particle to reach maximum height. (Neglect time of collision).
2ucosθg
2usinθg
u(sinθ+cosθ)g
2ug
The correct Answer is:C
After the elastic collision with inclined plane the projectile moves in vertical direction. The inclination of plane with horizontal is 45∘ thence velocity of particle just before collinsion should be horizontal. Time required to reach maximum height
=tAB+tBC=usinθg+ucosθg
Similar Questions
A particle is projected from the ground with velocity u making an angle θ with the horizontal. At half of its maximum heights,
View SolutionA particle is projected from the bottom of an inclined plane of inclination 30∘. At what angle α (from the horizontal) should the particle be projected to get the maximum range on the inclined plane.
View SolutionA particle is projected horizontally with a speed u from the top of plane inclined at an angle θ with the horizontal. How far from the point of projection will the particle strike the plane ?

View SolutionA particle is projected on an inclined plane with a speed u as shown in (Fig. 5.61). Find the range of the particle on the inclined plane.
 .
.
View SolutionA particle is projected from ground with speed u and at an angle θ with horizontal. If at maximum height from ground, the speed of particle is 1/2 times of its initial velocity of projection, then find its maximum height attained.
View SolutionA particle is projected with a speed u at an angle θ to the horizontal. Find the radius of curvature.
At the point where the particle is at a highest half of the maximum height H attained by it.
View SolutionA particle is projected up an inclines plane. Plane is inclined at an angle θ with horizontal and particle is projected at an angle α with horizontal. If particle strikes the plane horizontally prove that tanα=2tanθ
View SolutionA particle slides down a smooth inclined plane of elevation θ fixed in an elevator going up with an acceleration a0. The base of the incline has a length L. Find the time taken by the particle to reach the bottom.
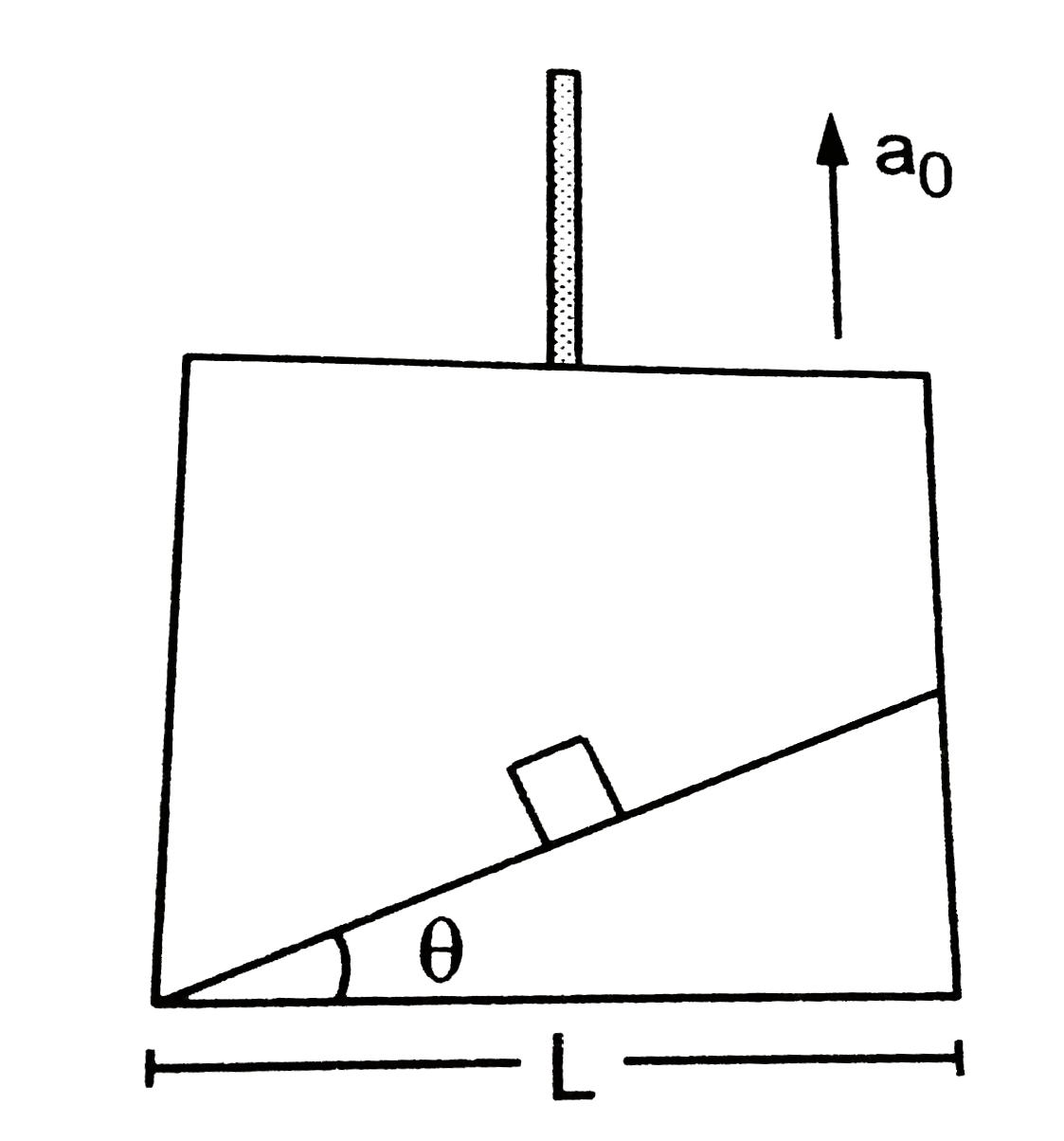
View SolutionA particle slides down a smooth inclined plane of elevation θ fixed in an elevator going up with an accelerationa0. The base of the incline has a length L.Find the time taken by the particle to reach the bottom.

View Solution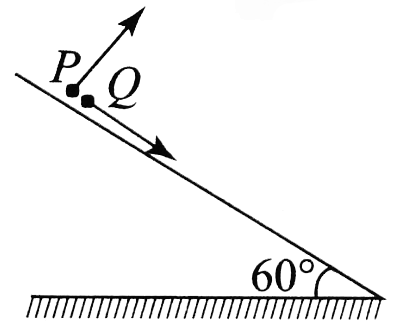
A particle P is projected from a point on the surface of smooth inclined plane (see figure). Simultaneously another particle Q is released on the smooth inclined plane from the same position. P and Q collide aftert=4. The speed of projection of P is
View Solution
