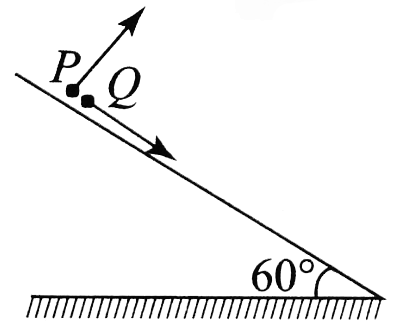
A particle P is projected from a point on the surface of smooth inclined plane (see figure). Simultaneously another particle Q is released on the smooth inclined plane from the same position. P and Q collide after $t = 4$ . The speed of projection of P is

$5 \frac{m}{s}$

$10 \frac{m}{s}$

$15 \frac{m}{s}$

$20 \frac{m}{s}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

It can be observed from figure that P and Q shall collide if the initial component of velocity of P along incline $u_{∣ ∣} = 0$ that is particle is projected perpendicular to incline.
Time of flight
$T = \frac{2 u ⊥}{g \cos θ} = \frac{2 u}{g \cos θ}$
$u = \frac{g T \cos θ}{2} = 10 \frac{m}{s}$

Updated on:21/07/2023

Class 12 PHYSICS QUESTION BANK

Similar Questions

A sphere is released on a smooth inclined plane from the top. When it moves down, its angular momentum is
View Solution
A ball is projected from point A with velocity $10 m s^{- 1}$ perpendicular to the inclined plane as shown in figure. Range of the ball on the inclined plane is

View Solution
A ball is projected from point A with velocity 20 m/s prependicular to the inclined plane as shown in figure. What is the range of the ball on the inclined plane ?

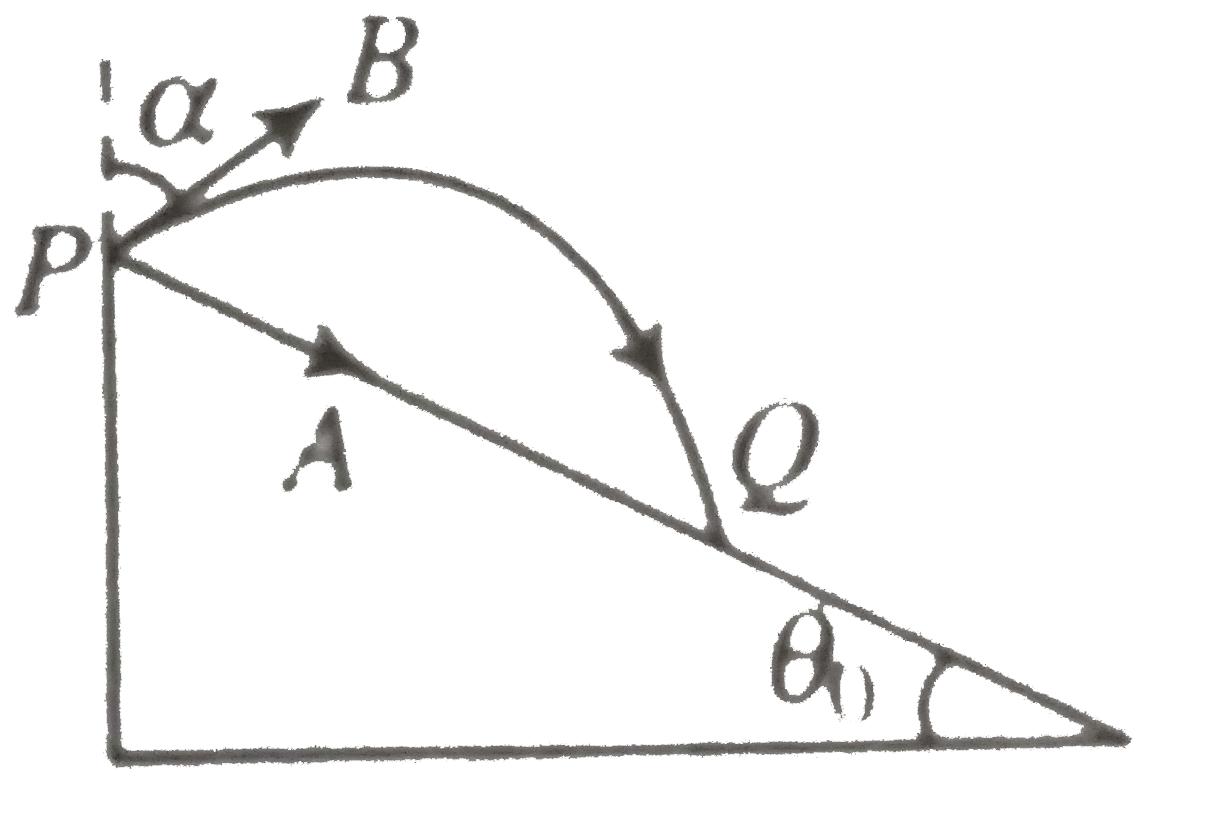
View Solution
Figure shows that particle A is projected from point P with velocity u along the plane and simultaneously another particle B with velocity v at an angle $α$ with vertical. The particles collide at point Q on the plane. Then

View Solution
A particle is projected from surface of the inclined plane with speed u and at an angle $θ$ with the horizontal. After some time the particle collides elastically with the smooth fixed inclined plane for the first time and subsequently moves in vertical direction. Starting from projection, find the time taken by the particle to reach maximum height. (Neglect time of collision).
View Solution
A particle is projected along an inclined plane as shown in figure. What is the speed of the particle when it collides at point A ? $(g = 10 \frac{m}{s^{2}})$

View Solution
Two particles P and Q are projected from two points in the same plane as shown. Find the condition for collision of two paricles.
View Solution
A particle is projected on an inclined plane with a speed $u$ as shown in (Fig. 5.61). Find the range of the particle on the inclined plane.
.
View Solution
For a given velocity of projection from a point on the inclined plane, the maximum range down the plane is three times the maximum range up the incline. Then find the angle of inclination of the inclined plane.
View Solution
A particle $P$ is to be projected from a fixed point $A$ on the ground with a fixed speed $u$ . Another particle $Q$ is also to be projected from a point $B$ which is directly above the point $A$ . The trajectory of the particle $Q$ touches all possible trajectories (for different angle of projection) of the particle $P$ in the vertical $x - y$ plane. Find the equation of trajectory of the particle $Q$ . (Take the point $A$ as origin, horizontal axis $x -$ axis and vertical axis $y -$ axis Consider the figure.)

View Solution

A particle P is projected from a point on the surface of smooth inclined plane (see figure). Simultaneously another particle Q is released on the smooth inclined plane from the same position. P and Q collide after t = 4 . The speed of projection of P is

The correct Answer is:B

It can be observed from figure that P and Q shall collide if the initial component of velocity of P along incline u ∣ ∣ = 0 that is particle is projected perpendicular to incline. Time of flight T = 2 u ⊥ g cos θ = 2 u g cos θ u = g T cos θ 2 = 10 m s

Similar Questions

Recommended Questions

A particle P is projected from a point on the surface of smooth inclined plane (see figure). Simultaneously another particle Q is released on the smooth inclined plane from the same position. P and Q collide after $t = 4$ . The speed of projection of P is