Two particles P and Q are projected from two points in the same plane as shown. Find the condition for collision of two paricles.
To find the condition for the collision of two particles P and Q projected from different points in the same plane, we will follow these steps:
Step 1: Understand the Problem
We have two particles, P and Q, projected from two different heights h1 and h2 with initial velocities u1 and u2 at angles θ1 and θ2 respectively. We need to determine the condition under which these two particles collide.
Step 2: Write the Velocity Components
For particle P:
- The horizontal component of velocity VPx=u1cos(θ1)
- The vertical component of velocity VPy=u1sin(θ1)
For particle Q:
- The horizontal component of velocity VQx=−u2cos(θ2) (negative because it is in the opposite direction)
- The vertical component of velocity VQy=u2sin(θ2)
Step 3: Relative Motion
To analyze the collision, we can consider the motion of particle P with respect to particle Q. The relative velocity of P with respect to Q is given by:
Vrel=VP−VQ
Thus,
Vrelx=u1cos(θ1)+u2cos(θ2)
Vrely=u1sin(θ1)−u2sin(θ2)
Step 4: Condition for Collision
For the two particles to collide, they must be at the same position at the same time. This means that the trajectory of particle P must intersect with that of particle Q.
Let d be the horizontal distance between the two particles at the time of projection. The condition for collision can be expressed in terms of the angles and heights:
tan(α)=VrelyVrelx=u1sin(θ1)−u2sin(θ2)u1cos(θ1)+u2cos(θ2)
Where α is the angle of the line connecting the two particles at the moment of collision.
Step 5: Relate to Heights
The vertical distance between the two particles at the time of collision can be expressed as:
h2−h1=dtan(α)
Substituting the expression for tan(α):
h2−h1=d⋅u1sin(θ1)−u2sin(θ2)u1cos(θ1)+u2cos(θ2)
Step 6: Final Condition
Rearranging gives us the final condition for collision:
(h2−h1)⋅(u1cos(θ1)+u2cos(θ2))=d⋅(u1sin(θ1)−u2sin(θ2))
We have two particles, P and Q, projected from two different heights h1 and h2 with initial velocities u1 and u2 at angles θ1 and θ2 respectively. We need to determine the condition under which these two particles collide.
For particle P:
- The horizontal component of velocity VPx=u1cos(θ1)
- The vertical component of velocity VPy=u1sin(θ1)
- The horizontal component of velocity VQx=−u2cos(θ2) (negative because it is in the opposite direction)
- The vertical component of velocity VQy=u2sin(θ2)
To analyze the collision, we can consider the motion of particle P with respect to particle Q. The relative velocity of P with respect to Q is given by:
Vrel=VP−VQ
Thus,
Vrelx=u1cos(θ1)+u2cos(θ2)
Vrely=u1sin(θ1)−u2sin(θ2)
For the two particles to collide, they must be at the same position at the same time. This means that the trajectory of particle P must intersect with that of particle Q.
tan(α)=VrelyVrelx=u1sin(θ1)−u2sin(θ2)u1cos(θ1)+u2cos(θ2)
Where α is the angle of the line connecting the two particles at the moment of collision.
The vertical distance between the two particles at the time of collision can be expressed as:
h2−h1=dtan(α)
Substituting the expression for tan(α):
h2−h1=d⋅u1sin(θ1)−u2sin(θ2)u1cos(θ1)+u2cos(θ2)
Rearranging gives us the final condition for collision:
(h2−h1)⋅(u1cos(θ1)+u2cos(θ2))=d⋅(u1sin(θ1)−u2sin(θ2))
Topper's Solved these Questions
- MOTION IN A PLANEBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - llustration 1 :
1 Videos
- MOTION IN A PLANEBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - Try yourself
48 Videos
- MOCK_TEST_17BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOCK_TEST_17EXERCISE - Example
15 Videos
- MOTION IN A STRAIGHT LINEBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - ASSIGNMENT (SECTION - D)
15 Videos
Similar Questions
Two particles are projected from two high rise buildings simultaneously as shown then find minimum distance between particles.

View SolutionTwo identical particles 1 and 2 are projected from surface of earth with same velocities in the directions shows in figure.
View SolutionTwo particles A and B are projected simultaneously in a vertical plane as shown in figure. They collide at time t in air. Write down two necessary equations for collision to take place.

View SolutionIn an elastic collision between two particles
View SolutionTwo particles of charges +Q and −Q are projected from the same point with a velocity v in a region of unifrom magnetic filed B such that the velocity vector makes an angle 'theta' with the magnetic filed Their masses are M and 2M respectively Then, they will meet again for the first time at a point whose distane from the point of projection is .
View SolutionTwo particles are projected from the two towers simultaneously, as shown in the figure. What should be value of 'd' for their collision.

View SolutionTwo particles A and B are projected from the same point in different direction in such a manner that their velocity vectors are shown in the diagram :−
 .
.
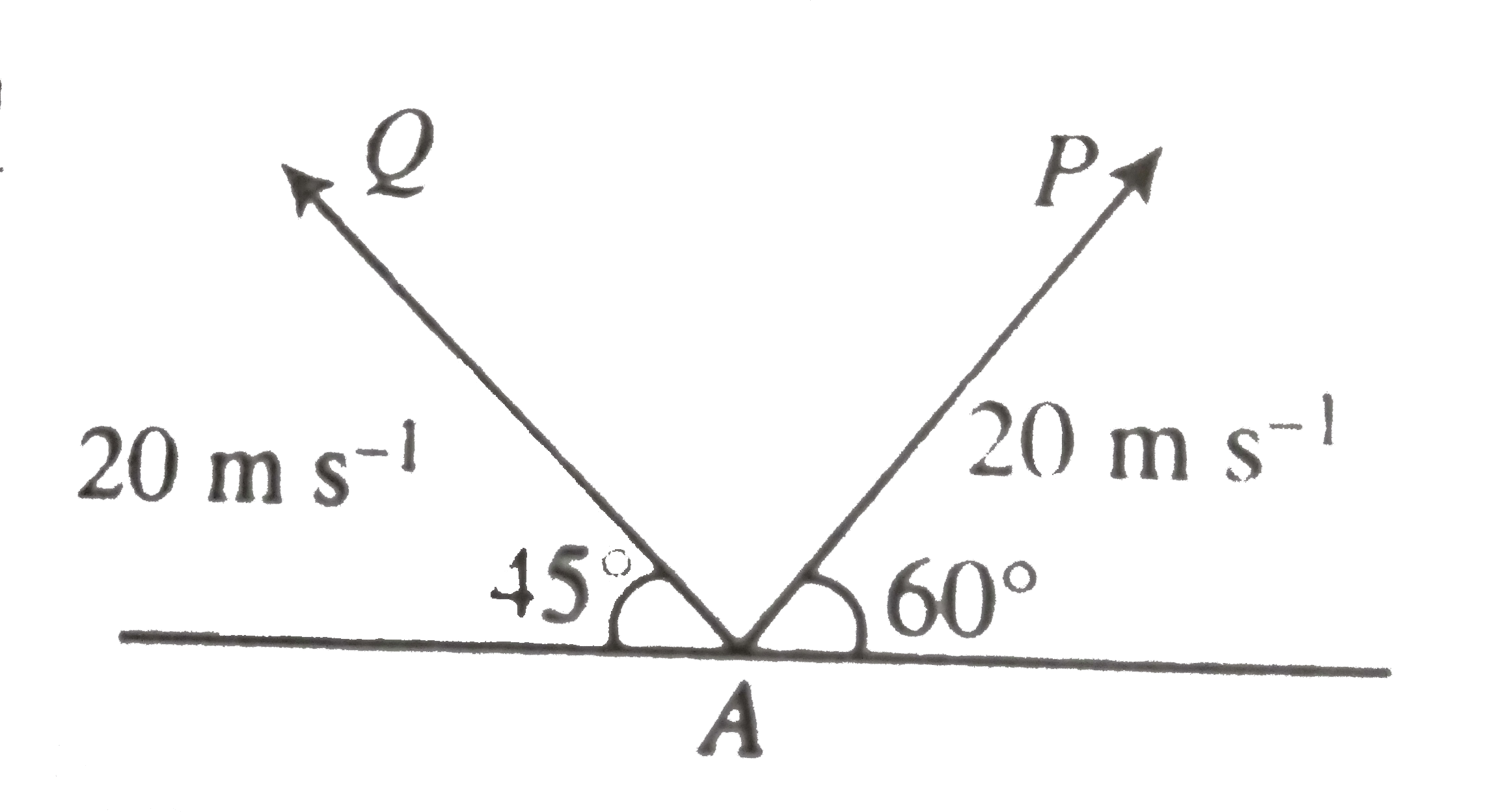
View SolutionTwo particles P and Q are projected simultaneously away from each other from a point A as shown in figure. The velocity of P relative to Q in ms−1 at the instant when the motion of P is horizontal is
View SolutionOn an inclined plane two particles AandB are projected with same speed at the same angle with the horizontal, particle A down and particle B up the plane. If the ratio of time of flight of AandB is cotθ, where θ is the angle at which B is projected measured from inclined plane, find the angle at which particles are projected.
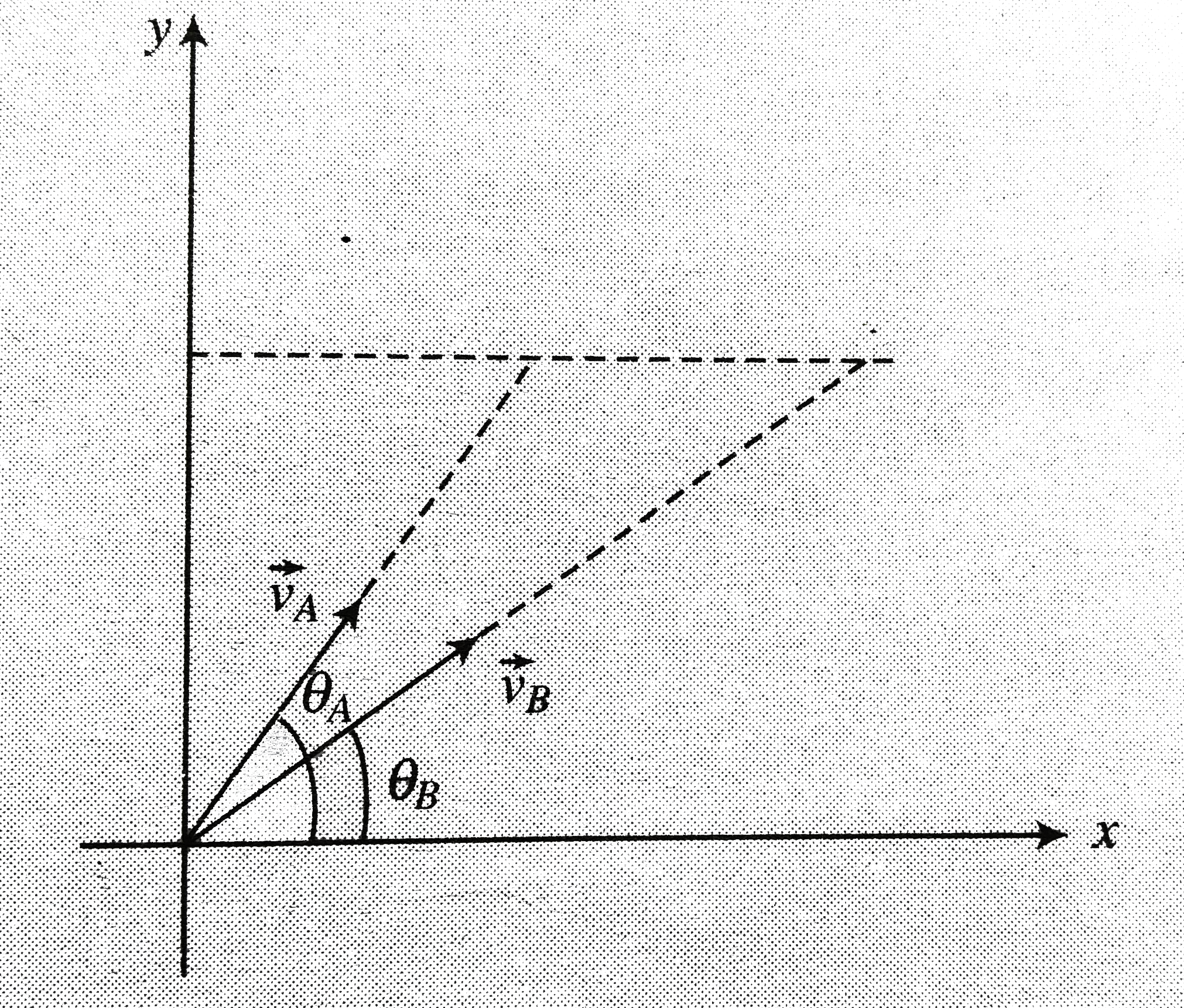
View SolutionTwo particles AandB are projected from the same point in different directions in such a manner that vertical components of their initial velocities are same (Fig. 5.8). Find the ratio of range.
 .
.
View Solution
