A particle is projected from point P on inclined plane OA perpendicular to it with certain velocity v. It this another inclined plane OB at point Q perpendicular to it. Point P and Q are at h1 and h2 height from ground. (α>β)
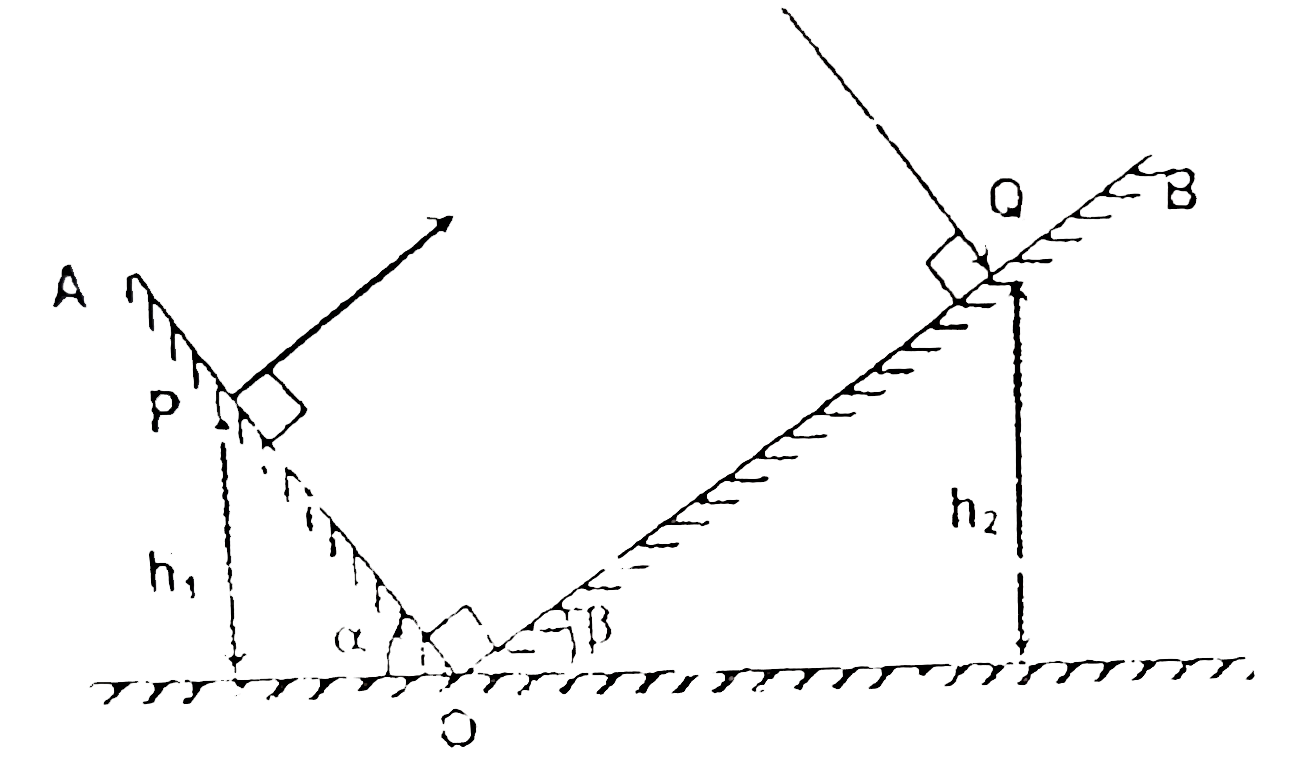
h1=h2
h1>h2
h1<h2
any of above depends on speed of projection.
perpendicular to OB, v'=−vsinθ(90∘−α−β)+gcosβt…..(i)
Parallel to OB, 0=vcos(90∘−α−β)−gsinβt……(ii)
on solving v'=vsinαsinβ
for α>β, v'>v, so by energy conservation h2<h1
Topper's Solved these Questions
- GMP ASSESMENTBook:FIITJEEChapter:GMP ASSESMENTExercise:Assertion & Reason
Explore 15 Videos
- GMP ASSESMENTBook:FIITJEEChapter:GMP ASSESMENTExercise:Multiple Question
Explore 58 Videos
- GMP ASSESMENTBook:FIITJEEChapter:GMP ASSESMENTExercise:Numerical Based
Explore 61 Videos
- GENERAL PHYSICSBook:FIITJEEChapter:GENERAL PHYSICSExercise:MATRIX MATCH TYPE
Explore 3 Videos
- GRAVITATIONBook:FIITJEEChapter:GRAVITATIONExercise:Numerical based Question
Explore 2 Videos
Similar Questions
A ball is projected from point A with velocity 10ms−1 perpendicular to the inclined plane as shown in figure. Range of the ball on the inclined plane is

View SolutionA particle is projected from point A perpendicular to inclined plane with a velocity 50m/s as shown in the figure. Particle strikes a vertical plane perpendicularly at point B. Time taken by particle in going from point A to point B is
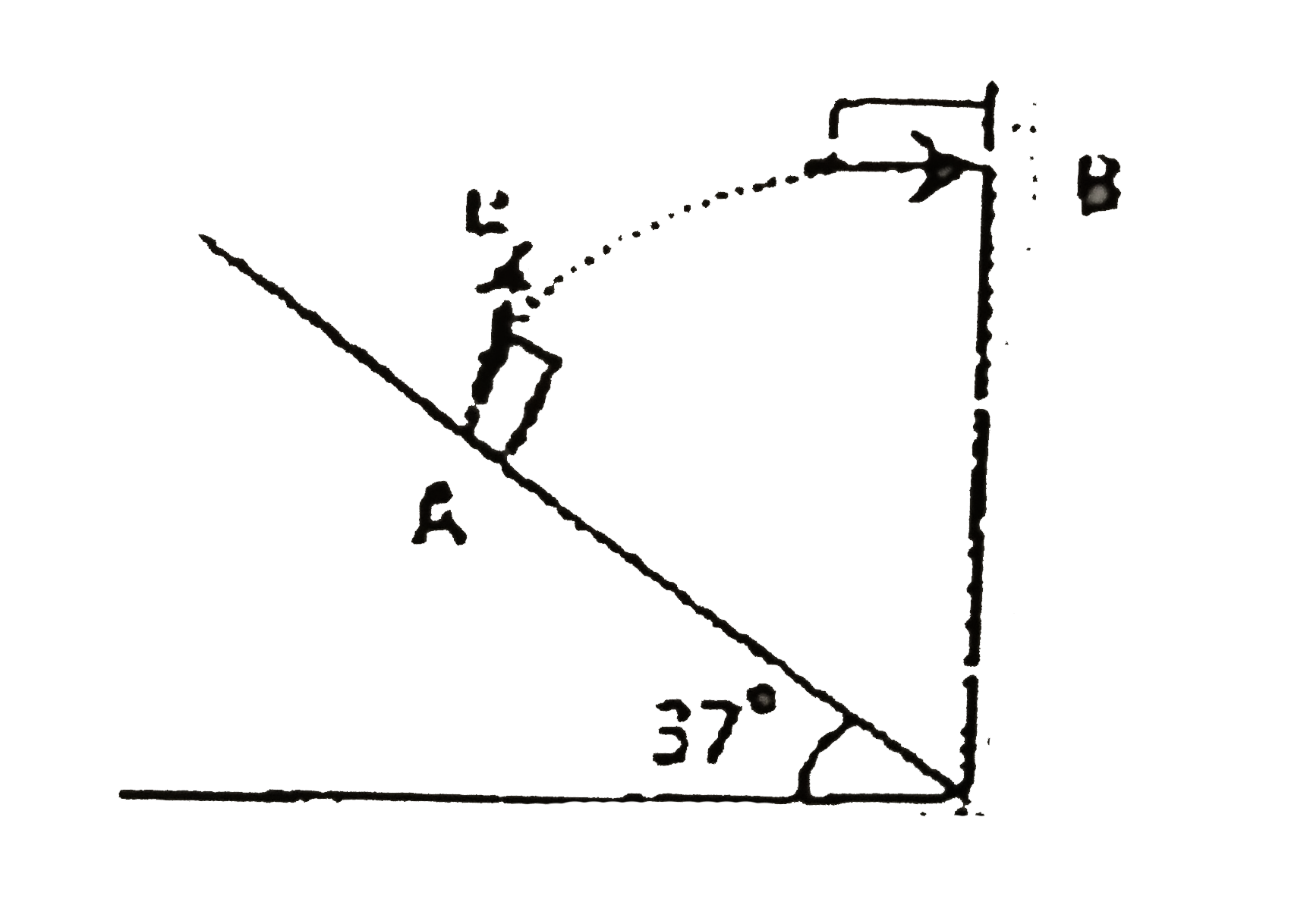
View Solution
Knowledge Check
A particle is projected with a velocity u from the foot of an inclined plane whose inclination to the horizon is β. It strikes. the plane at right angles if
Atan(α−β)=cotβB2tan(α−β)=cotβC2cot(α−β)=cotβDNone of theseA ball is projected from point A with velocity 10ms−1 perpendicular to the inclined plane as shown in figure. Range of the ball on the inclined plane is
 A403mB203mC123mD603m
A403mB203mC123mD603mA ball is projected from point A with velocity 10ms−1 perpendicular to the inclined plane as shown in figure. Range of the ball on the inclined plane is
 A403mB2013mC1320mD1340m
A403mB2013mC1320mD1340m
A valley has two walls inclined at 37° and 53° to the horizontal. A particle is projected from point P with a velocity of u=20m/s along a direction perpendicular to the incline wall OA. The Particle hits the incline surface RB perpendicularly at Q. Take g=10m/s2 and find:
(a) The time of flight of the particle.
(b) Vertical height h of the point P from horizontal surface OR.
[tan37∘=34]

View SolutionA particle is projected from a point P with a velocity v at an angle θ with horizontal. At a certain point Q it moves at right angles to its initial direction. Then
View SolutionA particle is projected from a point P with a velocity v at an angle θ with horizontal. At a certain point Q it moves at right angles to its initial direction. Then
View SolutionA projectile is projected on an inclined plane as shown in figure. 'D' is a point of maximum height from inclined plane then :

View SolutionA particle is projected from a point P with a velocity v at an angle θ with horizontal. At a certain point Q it moves at right angles to its initial direction. Then
View Solution

