A ball is projected with velocity u at right angle to the slope which inclined at an angle α with the horizontal. The distance x along the inclined plane that it will travell before again striking the slope is-
2u2gcosα
2u2gtanα
2u2gtanαcosα
2u2gtanαsinα
The correct Answer is:A
To solve the problem of a ball projected at right angles to a slope inclined at an angle α with the horizontal, we will follow these steps:
Step 1: Understand the Problem
The ball is projected vertically upward with an initial velocity u at an angle α to the horizontal. We need to find the distance x along the inclined plane that the ball travels before it strikes the slope again.
Step 2: Identify Forces and Components
When the ball is projected, the gravitational force g acts downward. We can resolve this gravitational force into two components relative to the inclined plane:
- Perpendicular to the slope: gcosα
- Parallel to the slope: gsinα
Step 3: Calculate Time of Flight
The time t taken for the ball to reach its highest point (where its vertical velocity becomes zero) can be calculated using the equation:
v=u+at
Here, v=0 at the highest point, a=−g (acting downwards), and u is the initial vertical velocity. Thus,
0=u−gt⟹t=ug
Since the ball will take the same time to come down, the total time of flight T is:
T=2t=2ug
Step 4: Calculate the Distance Along the Incline
The distance x along the incline can be calculated using the kinematic equation for displacement:
s=ut+12at2
In this case, the initial velocity along the incline is 0 (since it is projected vertically), and the acceleration along the incline is gsinα. Therefore,
x=12gsinα(2ug)2
Substituting the value of T:
x=12gsinα⋅4u2g2
Simplifying this gives:
x=2u2sinαg
Step 5: Final Expression
Thus, the distance x along the inclined plane that the ball will travel before striking the slope again is:
x=2u2sinαgcosα
The ball is projected vertically upward with an initial velocity u at an angle α to the horizontal. We need to find the distance x along the inclined plane that the ball travels before it strikes the slope again.
When the ball is projected, the gravitational force g acts downward. We can resolve this gravitational force into two components relative to the inclined plane:
- Perpendicular to the slope: gcosα
- Parallel to the slope: gsinα
The time t taken for the ball to reach its highest point (where its vertical velocity becomes zero) can be calculated using the equation:
v=u+at
Here, v=0 at the highest point, a=−g (acting downwards), and u is the initial vertical velocity. Thus,
0=u−gt⟹t=ug
Since the ball will take the same time to come down, the total time of flight T is:
T=2t=2ug
The distance x along the incline can be calculated using the kinematic equation for displacement:
s=ut+12at2
In this case, the initial velocity along the incline is 0 (since it is projected vertically), and the acceleration along the incline is gsinα. Therefore,
x=12gsinα(2ug)2
Substituting the value of T:
x=12gsinα⋅4u2g2
Simplifying this gives:
x=2u2sinαg
Thus, the distance x along the inclined plane that the ball will travel before striking the slope again is:
x=2u2sinαgcosα
Similar Questions
A projectile is fired with a velocity v at right angle to the slope inclined at an angle θ with the horizontal. The range of the projectile along the inclined plane is

View SolutionA projectile is fired with a velocity u at right angles to the slope, which is inclined at an angle θ with the horizontal. Derive an expression for the distance R to the point of impact.
 .
.
View SolutionA ball is projected from point A with velocity 20 m/s prependicular to the inclined plane as shown in figure. What is the range of the ball on the inclined plane ?

View SolutionA ball is projected horizontally with a speed v from the top of the plane inclined at an angle 45∘ with the horizontal. How far from the point of projection will the ball strikes the plane?
View SolutionA particle is projected horizontally with a speed u from the top of plane inclined at an angle θ with the horizontal. How far from the point of projection will the particle strike the plane ?

View SolutionA ball is projected from point A with velocity 10ms−1 perpendicular to the inclined plane as shown in figure. Range of the ball on the inclined plane is

View SolutionA particle is projected in air at an angle β to a surface which itself is inclined at an angle α to the horizontal (Fig. 2 (EP). 26)
(a) Find an expression for range on the plane surface (distance on the plane from the point of projection at which particle will hit the surface). (b) Time of flight. 9c ) β at which range will be maximum.
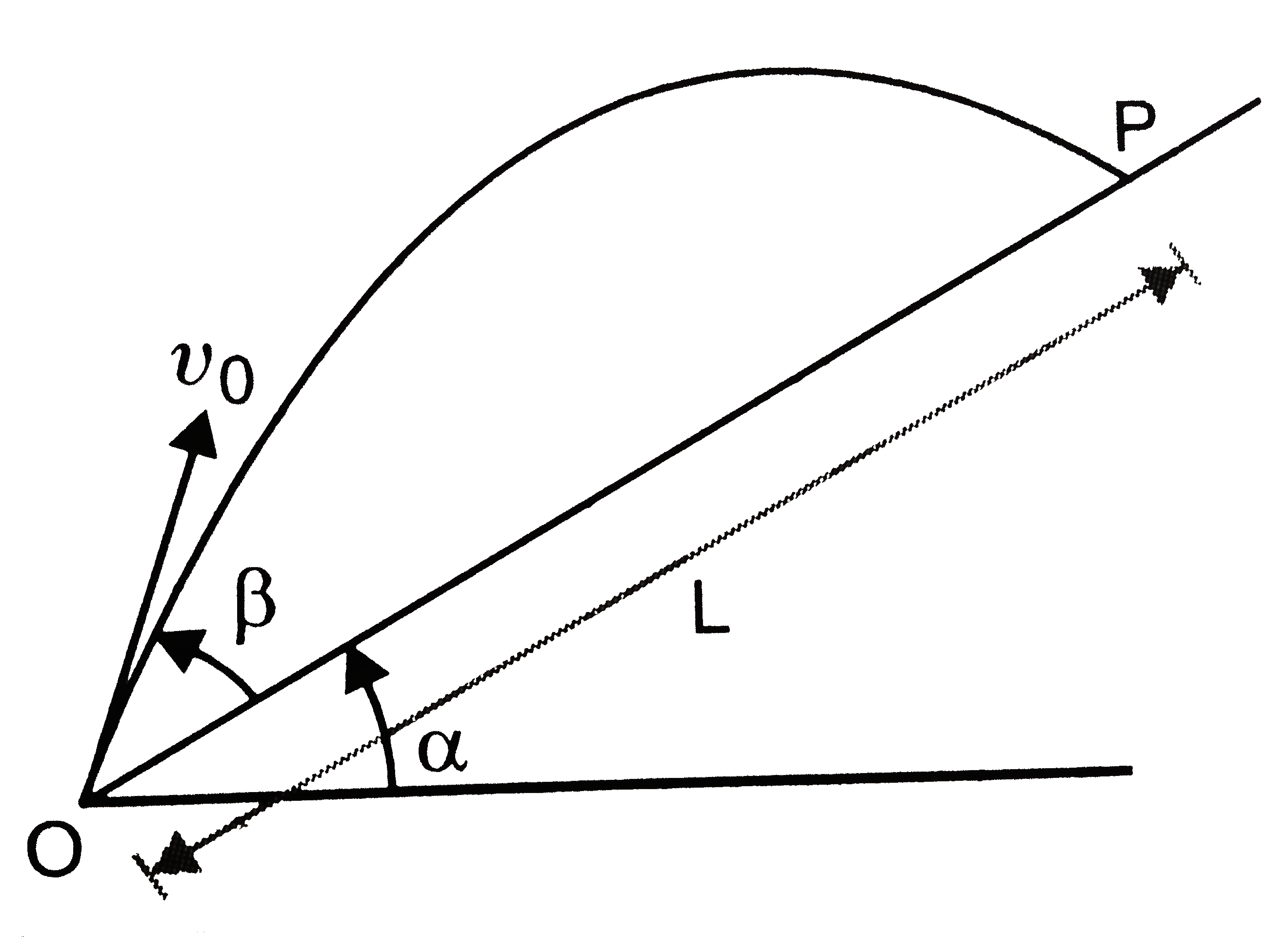
View SolutionA ball starts falling freely from a height h from a point on the inclined plane forming an angle α with the horizontal as shown. After collision with the incline it rebounds elastically off the plane. Then it again strikes the incline at

View SolutionA particle is projected with a velocity u making an angle θ with the horizontal. The instantaneous power of the gravitational force
View SolutionA trolley containing a liquid slides down a smooth inclined plane of angle α with the horizontal. Find the angle of inclination θ of the free surface with the horizontal.

View Solution