The graph of a line in the xy-plane passes through the point (1, 4) and crosses the x-axis at the point (2, 0). The line crosses the y-axis at the point (0, b). What is the value of b ?
Since the line passes through the point (2, 0), its equation is of the form y = m(x − 2). The coordinates of the point (1, 4) must also satisfy this equation. So 4 = m(1 − 2), or m = −4. Substituting −4 for m in the equation of the line gives y = −4(x – 2), or equivalently y = −4x + 8. Therefore, b = 8.
Alternate approach: Given the coordinates of two points through which the line passes, the slope of the line is 4−01−2=−4. So, the equation of the line is of the form y = −4x + b. Since (2, 0) satisfies this equation, 0 = −4(2) + b must be true. Solving this equation for b gives b = 8.
Similar Questions
Knowledge Check
The graph of a line in the xy-plane passes through the points (5,4)and(3,12). Which of the following equations describes the line ?
Ay=74x+194By=−74x−194Cy=74x−194Dy=46x+87Of a line passes through the points (5, 3) and (8, -1), at what point will this line intersect the y - axis ?
A(0,8.33)B(0,8.67)C(0,9.00)D(0,9.67)The graph of a line in the xy-plane has slope 2 and contains the point (1, 8). The graph of a second line passes through the points (1, 2) and (2, 1). If the two lines intersect at the point (a, b), what is the value of a+b ?
A4B3C-1D-4
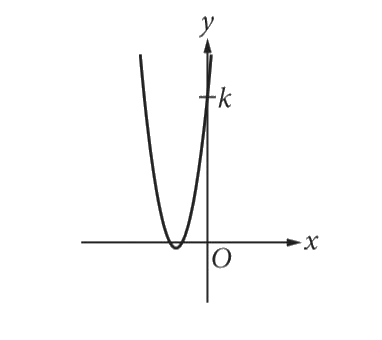
The graph of y=2x2+10x+12 is shown. If the graph crosses the y -axis at the point ( 0, k) , what is the value of k ?
View SolutionThe graph of a line in the xy-plane passes through the points (5, -5) and (1, 3). The graph of a second line has a slope of 6 and passes though the point (0, 1). If the two lines intersects at (p, q), what is the value of p+q?
View SolutionFind the equation of the line passing through the point (2, 2) and inclined to x-axis at 450.
View SolutionThe graph of a line in the xy-plane passes through the points (5,−5)and(1,3). The graph of a second line has a slope of 6 and passes through the point (−1,15). If the two lines intersect at (p,q), what is the value of p+q?
View SolutionThe line passing through the points (5,1,a)and(3,b,1) crosses the YZ-plane at the point (0,172,−132). Then,
View Solution
