A man sitting in a bus travelling in a direction from west to east with a speed of 40km/h observes that the rain-drops are falling vertically down. To the another man standing on ground the rain will appear
to fall vertically down
to fall at an angle going from west to east
To fall at an angle going from east to west
The information given is insufficient to dicide the direction of rain.
The correct Answer is:B
To solve the problem, we need to analyze the situation using vector components. Here’s a step-by-step solution:
Step 1: Understand the scenario
A man is sitting in a bus moving from west to east at a speed of 40 km/h. He observes the raindrops falling vertically downwards. This means that, from his frame of reference, the horizontal component of the rain's velocity must equal the bus's speed.
Hint: Identify the reference frames involved: the man in the bus and the man on the ground.
Step 2: Define the velocities
Let:
- Vbus=40km/h (velocity of the bus towards the east)
- Vr = velocity of the rain with respect to the ground (which we need to find)
- Vr,man = velocity of the rain with respect to the man in the bus (which he sees as vertical)
Hint: Use vector notation to represent the velocities. The bus's velocity can be represented as 40^i.
Step 3: Set up the equation
From the perspective of the man in the bus, the rain appears to fall vertically. Therefore, we can express the velocity of the rain as:
Vr,man=Vr−Vbus
Since the rain appears to fall vertically for the man in the bus, the horizontal component of the rain's velocity must be equal to the speed of the bus:
Vr,man=0^i+Vr,y^j
This means:
Vr−40^i=0^i+Vr,y^j
Hint: Recognize that the vertical component of the rain's velocity is what we need to isolate.
Step 4: Solve for the rain's velocity
From the equation above, we can separate the components:
1. Horizontal component: Vr,x−40=0 → Vr,x=40km/h
2. Vertical component: Vr,y is unknown and represents the speed of the rain falling downwards.
Thus, we can express the velocity of the rain as:
Vr=40^i+Vr,y^j
Hint: The rain's velocity has both horizontal and vertical components.
Step 5: Determine the angle of the rain's path
To find the angle at which the rain appears to fall to the observer on the ground, we can use the tangent function:
tan(θ)=Vr,yVr,x
Substituting Vr,x=40km/h:
tan(θ)=Vr,y40
The angle θ will be the angle of the rain's path with respect to the vertical.
Hint: Use trigonometric functions to relate the components of the velocity to the angle.
Conclusion
The rain will appear to fall at an angle to the vertical for the observer on the ground, specifically at an angle that can be calculated using the vertical component of the rain's velocity.
Final Answer: The rain will appear to fall at an angle from the vertical towards the east for the observer on the ground.
A man is sitting in a bus moving from west to east at a speed of 40 km/h. He observes the raindrops falling vertically downwards. This means that, from his frame of reference, the horizontal component of the rain's velocity must equal the bus's speed.
Let:
- Vbus=40km/h (velocity of the bus towards the east)
- Vr = velocity of the rain with respect to the ground (which we need to find)
- Vr,man = velocity of the rain with respect to the man in the bus (which he sees as vertical)
From the perspective of the man in the bus, the rain appears to fall vertically. Therefore, we can express the velocity of the rain as:
Vr,man=Vr−Vbus
Vr,man=0^i+Vr,y^j
Vr−40^i=0^i+Vr,y^j
From the equation above, we can separate the components:
1. Horizontal component: Vr,x−40=0 → Vr,x=40km/h
2. Vertical component: Vr,y is unknown and represents the speed of the rain falling downwards.
Vr=40^i+Vr,y^j
To find the angle at which the rain appears to fall to the observer on the ground, we can use the tangent function:
tan(θ)=Vr,yVr,x
tan(θ)=Vr,y40
The rain will appear to fall at an angle to the vertical for the observer on the ground, specifically at an angle that can be calculated using the vertical component of the rain's velocity.
Similar Questions
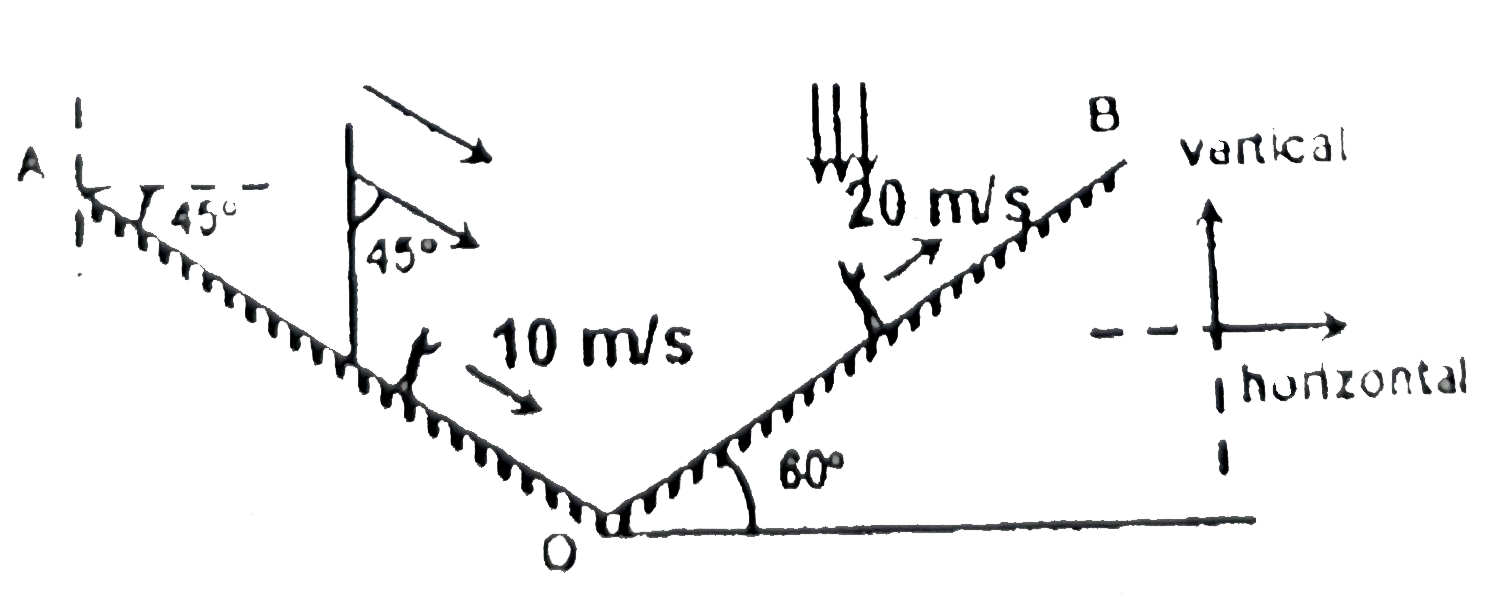
There are two incline planes AO and OB inclined at 45∘ and 60∘ respectively with the horizontal as shown in the figure. When a man moves on the inclined plane AO he is oberves that the rain drops are falling 45∘ with the vertical. When the man moves on the inclined plane OB, he observes that the raindrops are falling vertically downward with the horizontal. Then actual speed of rain is
View SolutionA man starts running along a straight road with uniform velocity observes that the rain is falling vertically downward. If he doubles his speed, he finds that the rain is coming at an angle θ to the vertical. The velocity of rain with respect to the ground is :
View SolutionA man starts running along a straight road with uniform velocity observes that the rain is falling vertically downward. If he doubles his speed, he finds that the rain is coming at an angle θ to the vertical. The velocity of rain with respect to the ground is :
View SolutionA car with a vertical windshield moves in a rain storm at a speed of 40 km/hr. The rain drops fall vertically with constant speed of 20 m/s. The angle at which rain drops strike the windshield is -
View SolutionA man walking with a speed of 3 km/h finds the rain drops falling vertically downwards. When the man increases his speed to 6km/h he find that the rain drops are falling making an angle of 30∘ with the vertical . Find the speed of the rain drops ( in km/h)
View SolutionRain is falling vertically downwards with respect to ground. If a girl running on the ground with speed 3 km/h observes the rain is falling with speed 5 km/h then actual speed of rain is
View SolutionA man moving with 5ms−1 observes rain falling vertically at the rate of 10ms−1. Find the speed and direction of the rain with respect to ground.
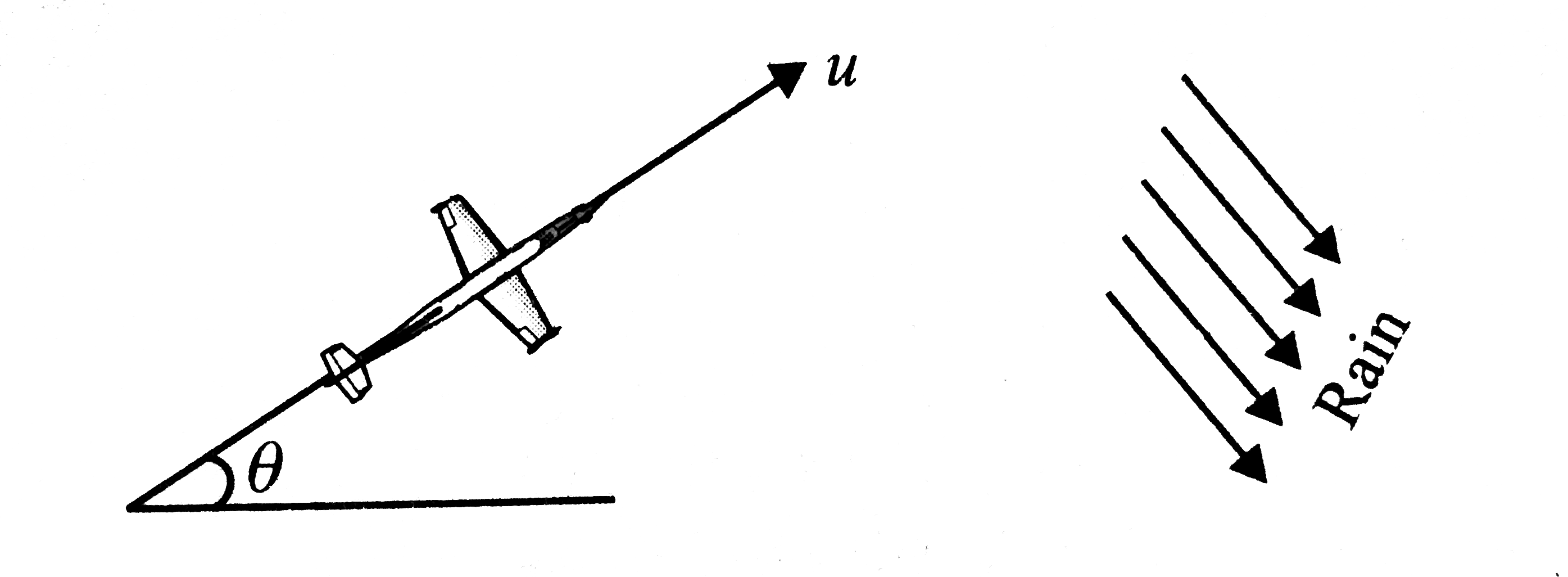
View SolutionRain is falling with a sped of 12√2m/s at an angle 45∘ with the vertical line. A man in a glider going at a speed of u at an angle of 37∘ with respect to the ground. Find the speed of the glider so that rain appears to him falling vertically. Consider the motion of the glider and rain drops in the same vertical plane.
View SolutionTo a stationary man, rain appears to be falling at his back at an angle 30∘ with the vertical. As he starts moving forward with a speed of 0.5ms−1, he finds that the rain is falling vertically.
The speed of rain with respect to the stationary man is.
View SolutionTo a stationary man, rain appears to be falling at his back at an angle 30∘ with the vertical. As he starts moving forward with a speed of 0.5ms−1, he finds that the rain is falling vertically.
The speed of rain with respect to the moving man is.
View Solution
