In the climax of a movie, the hero jumps from a helicopter and the villain chasing the hero also jumps from the same level . After sometime when they come at same horizontal level, the villain fires bullet horizontally towards the hero, Both were falling with constant acceleration 2(m)/(s^2), because of parachute, Assuming the hero to be within the range of bullet, which of the following is correct.
bullet will hit the hero
bullet will pass above the hero
bullet will pass below the hero
bullet will definitely hit the hero, if both were falling with constant acceleration g instead of 2ms2
The correct Answer is:C
To solve the problem, we need to analyze the motion of both the hero and the villain, as well as the bullet fired by the villain.
1. Identify the Initial Conditions:
- Both the hero and the villain jump from the same height and fall with a constant downward acceleration of 2m/s2 due to their parachutes.
2. Acceleration of the Bullet:
- When the villain fires the bullet, it will experience a downward acceleration due to gravity, which is approximately g=10m/s2.
3. Relative Motion:
- Since both the hero and the villain are falling with an acceleration of 2m/s2, we can say that they are both in free fall but with different accelerations compared to the bullet.
4. Time of Flight:
- When the villain fires the bullet horizontally, it will start falling downwards with an acceleration of 10m/s2. The bullet will fall faster than the hero, who is falling at 2m/s2.
5. Comparison of Positions:
- As time progresses, the vertical position of the hero can be described by the equation:
yh=h−12⋅2⋅t2
- The vertical position of the bullet can be described by:
yb=h−12⋅10⋅t2
- Here, h is the initial height from which both the hero and the bullet start falling.
6. Finding the Difference in Positions:
- The difference in the vertical positions of the bullet and the hero at any time t can be calculated as:
yb−yh=(h−12⋅10⋅t2)−(h−12⋅2⋅t2)
- Simplifying this gives:
yb−yh=12⋅(10−2)⋅t2=12⋅8⋅t2=4t2
- This means that the bullet is falling 4t2 meters below the hero at any time t.
7. Conclusion:
- Since the bullet falls faster than the hero, it will pass below the hero when fired. Therefore, the correct conclusion is that the bullet will not hit the hero, as it will fall below him.
Final Answer:
The bullet will pass below the hero.
- Both the hero and the villain jump from the same height and fall with a constant downward acceleration of 2m/s2 due to their parachutes.
- When the villain fires the bullet, it will experience a downward acceleration due to gravity, which is approximately g=10m/s2.
- Since both the hero and the villain are falling with an acceleration of 2m/s2, we can say that they are both in free fall but with different accelerations compared to the bullet.
- When the villain fires the bullet horizontally, it will start falling downwards with an acceleration of 10m/s2. The bullet will fall faster than the hero, who is falling at 2m/s2.
- As time progresses, the vertical position of the hero can be described by the equation:
yh=h−12⋅2⋅t2
- The vertical position of the bullet can be described by:
yb=h−12⋅10⋅t2
- Here, h is the initial height from which both the hero and the bullet start falling.
- The difference in the vertical positions of the bullet and the hero at any time t can be calculated as:
yb−yh=(h−12⋅10⋅t2)−(h−12⋅2⋅t2)
- Simplifying this gives:
yb−yh=12⋅(10−2)⋅t2=12⋅8⋅t2=4t2
- This means that the bullet is falling 4t2 meters below the hero at any time t.
- Since the bullet falls faster than the hero, it will pass below the hero when fired. Therefore, the correct conclusion is that the bullet will not hit the hero, as it will fall below him.
The bullet will pass below the hero.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENGAGE PHYSICS DPPEXERCISE - subjective type51videos
CENGAGE PHYSICS DPP
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENGAGE PHYSICS DPPEXERCISE - Multiple correct Answer Type54videos
CENGAGE PHYSICS DPP
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CAPACITOR AND CAPACITANCEEXERCISE - Integer5videos
CAPACITOR AND CAPACITANCE
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Single Answer Correct Type22videos
COULOMB LAW AND ELECTRIC FIELD
Similar Questions
A boy and a block, both of same mass, are suspended at the same horizontal level, from each end of a light string that moves over a frictionless pulley as shown. The boy start moving upward with an acceleration 2.5m/s2 relative the rope. If the block is to travel a total distance 10m before reaching at the pulley, the time taken by the block in doing so is equal to:
 View Solution
View SolutionTwo particles one of mass m and the other of mass 2 m are projected horizontally towards each other from the same level above the ground with velocities 10 m/s and 5 m/s respectively . They collide in air and stick to each other . The distance from A , where the combined mass finally land is
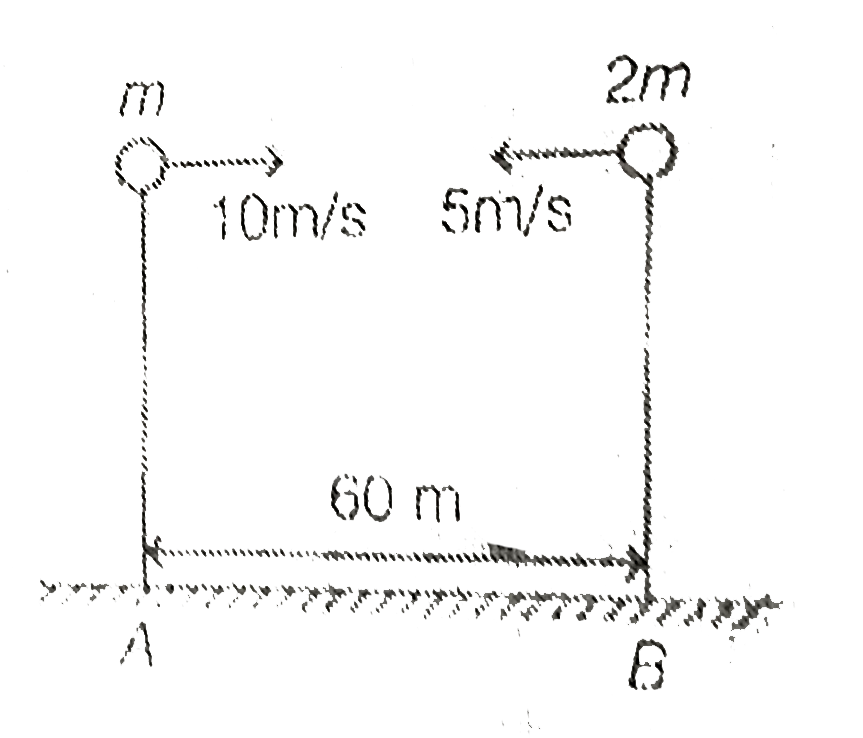 View Solution
View SolutionTwo particles, one of mass m and the other of mass 2m, are projected horizontally towards each other from the same level above the ground with velocities 10 m/s and 5 m/s, respectively. They collide in air and stick to each other. The distance of the combined mass from point A is
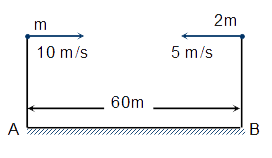 View Solution
View SolutionA man is standing on a road and observes that rain is failing at angle 45∘ with the vertical. The man starts running on the road with constant acceleration 0.5m/s2. After a certain time from the start of the motion, it appears to him that rain is still falling at angle 45∘ with the vertical, with speed 2√2m/s. Motion of the man is in the same vertical plane in which the rain is falling. Then which of the following staement(s) are true.
View SolutionTwo particles were projected one by one with the same initial velocity from the same point on level ground. They follow the same parabolic trajectory and are found to be in the same horizontal level, separated by a distance of 1m,2s after the second partice was projected. Assume that the horizontal component of their velocities is 0.5ms−1. Find
(a) the horizontal range of the parabolic path.
(b) the maximum height for the parabolic path.View SolutionTwo persons, A of mass 60kg and B of mass 40kg, are standing on a horizontal platform of mass 50kg. The platform is supported on wheels on a horizontal frictionless surface and is initially at rest. Consider the following situations.

(i) Both A and B jump from the platform simultaneously and in the same horizontal direction.
(ii) A jumps first in a horizontal direction and after a few seconds B also jumps in the same direction. In both the situations above, just after the jump, the person (A or B) moves away from the platform with a speed of 3m/s relative to the platform and along the horizontal.
In situation (i), just after both A and B jump from the platform, velocity of centre of mass of the system (A,B and the platform) isView SolutionTwo racing cars 'A' and 'B' having masses 'M' and '2m' respectively start running from the starting line on a horizontal plane.Both cars 'A' and B' have same speed 'V' which is constant through out the journey. The track of the two cars are the arcs of concentric circle having centres O1 and O2 as shwon in figure with data. The friction coefficient of the two cars with the road is same. There is a finishing line at the end of the arc. Using these informations solve the following questions.

Which of the following statements is incorrect.View SolutionA circus wishes to develop a new clown act. Fig. (1) shows a diagram of the proposed setup. A clown will be shot out of a cannot with velocity v0 at a trajectory that makes an angle θ=45∘ with the ground. At this angile, the clown will travell a maximum horizontal distance. The cannot will accelerate the clown by applying a constant force of 10,000N over a very short time of 0.24s. The height above the ground at which the clown begins his trajectory is 10m.

A large hoop is to be suspended from the celling by a massless cable at just the right place so that the clown will be able to dive through it when he reaches a maximum height above the ground. After passing through the hoop he will then continue on his trajectory until arriving at the safety net. Fig (2) shows a graph of the vertical component of the clown's velocity as a function of time between the cannon and the hoop. Since the velocity depends on the mass of the particular clown performing the act, the graph shows data for serveral different masses.

The slope of the line segments plotted in figure 2 is a figure constant. Which one of the following physical quantities does this slope represent?View SolutionA circus wishes to develop a new clown act. Fig. (1) shows a diagram of the proposed setup. A clown will be shot out of a cannot with velocity v0 at a trajectory that makes an angle θ=45∘ with the ground. At this angile, the clown will travell a maximum horizontal distance. The cannot will accelerate the clown by applying a constant force of 10,000N over a very short time of 0.24s. The height above the ground at which the clown begins his trajectory is 10m.
A large hoop is to be suspended from the celling by a massless cable at just the right place so that the clown will be able to dive through it when he reaches a maximum height above the ground. After passing through the hoop he will then continue on his trajectory until arriving at the safety net. Fig (2) shows a graph of the vertical component of the clown's velocity as a function of time between the cannon and the hoop. Since the velocity depends on the mass of the particular clown performing the act, the graph shows data for serveral different masses.
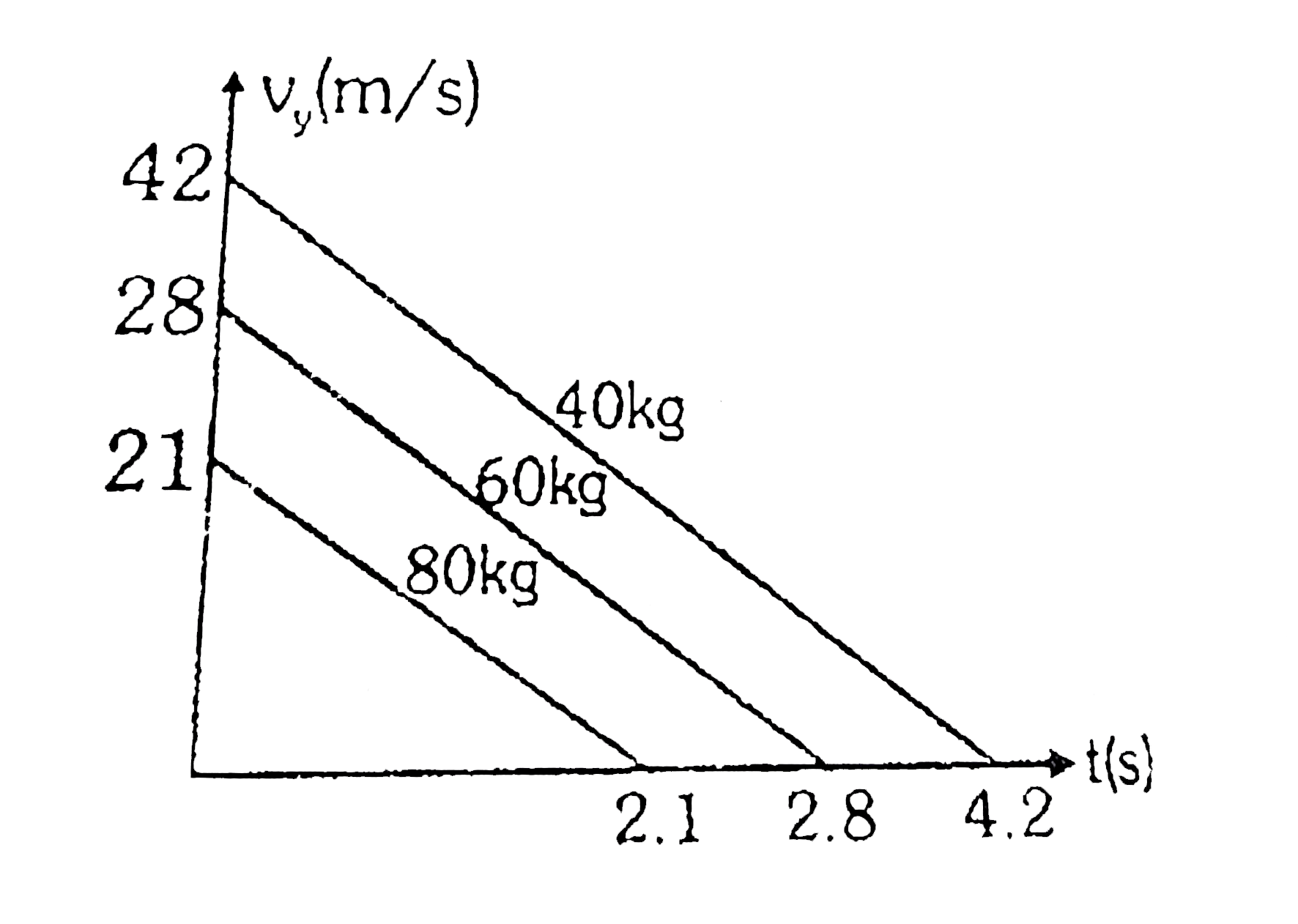
From figure 2, approximately how much time will it take for clown with a mass of 60 kg to reach the safety net located 10m below the height of the cannot?View SolutionA circus wishes to develop a new clown act. Fig. (1) shows a diagram of the proposed setup. A clown will be shot out of a cannot with velocity v0 at a trajectory that makes an angle θ=45∘ with the ground. At this angile, the clown will travell a maximum horizontal distance. The cannot will accelerate the clown by applying a constant force of 10,000N over a very short time of 0.24s. The height above the ground at which the clown begins his trajectory is 10m.

A large hoop is to be suspended from the celling by a massless cable at just the right place so that the clown will be able to dive through it when he reaches a maximum height above the ground. After passing through the hoop he will then continue on his trajectory until arriving at the safety net. Fig (2) shows a graph of the vertical component of the clown's velocity as a function of time between the cannon and the hoop. Since the velocity depends on the mass of the particular clown performing the act, the graph shows data for serveral different masses.

If the mass of a clown doubles, his initial kinetic energy, mv20/2, will :-View Solution
