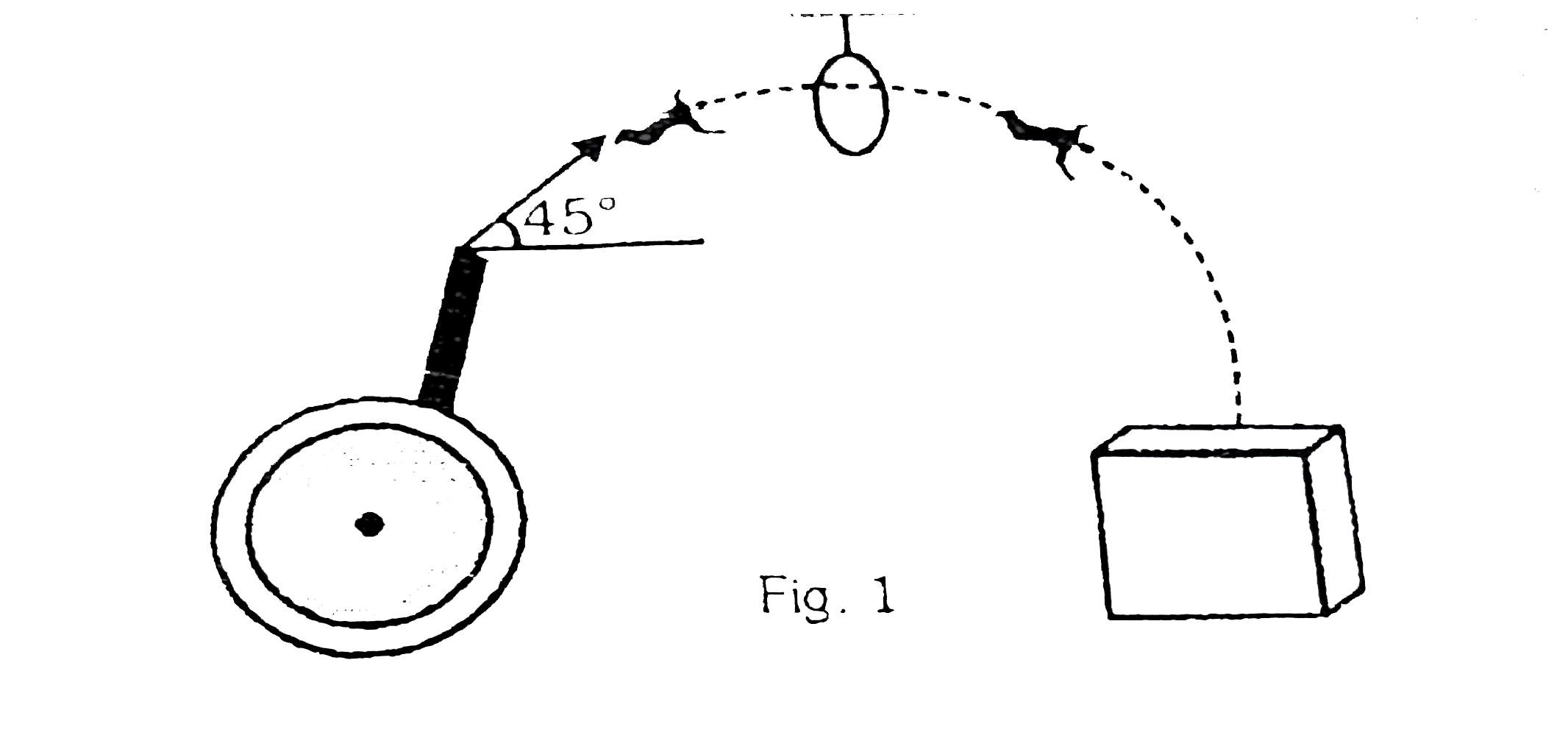
A circus wishes to develop a new clown act. Fig. (1) shows a diagram of the proposed setup. A clown will be shot out of a cannot with velocity v0 at a trajectory that makes an angle θ=45∘ with the ground. At this angile, the clown will travell a maximum horizontal distance. The cannot will accelerate the clown by applying a constant force of 10,000N over a very short time of 0.24s. The height above the ground at which the clown begins his trajectory is 10m.
A large hoop is to be suspended from the celling by a massless cable at just the right place so that the clown will be able to dive through it when he reaches a maximum height above the ground. After passing through the hoop he will then continue on his trajectory until arriving at the safety net. Fig (2) shows a graph of the vertical component of the clown's velocity as a function of time between the cannon and the hoop. Since the velocity depends on the mass of the particular clown performing the act, the graph shows data for serveral different masses.
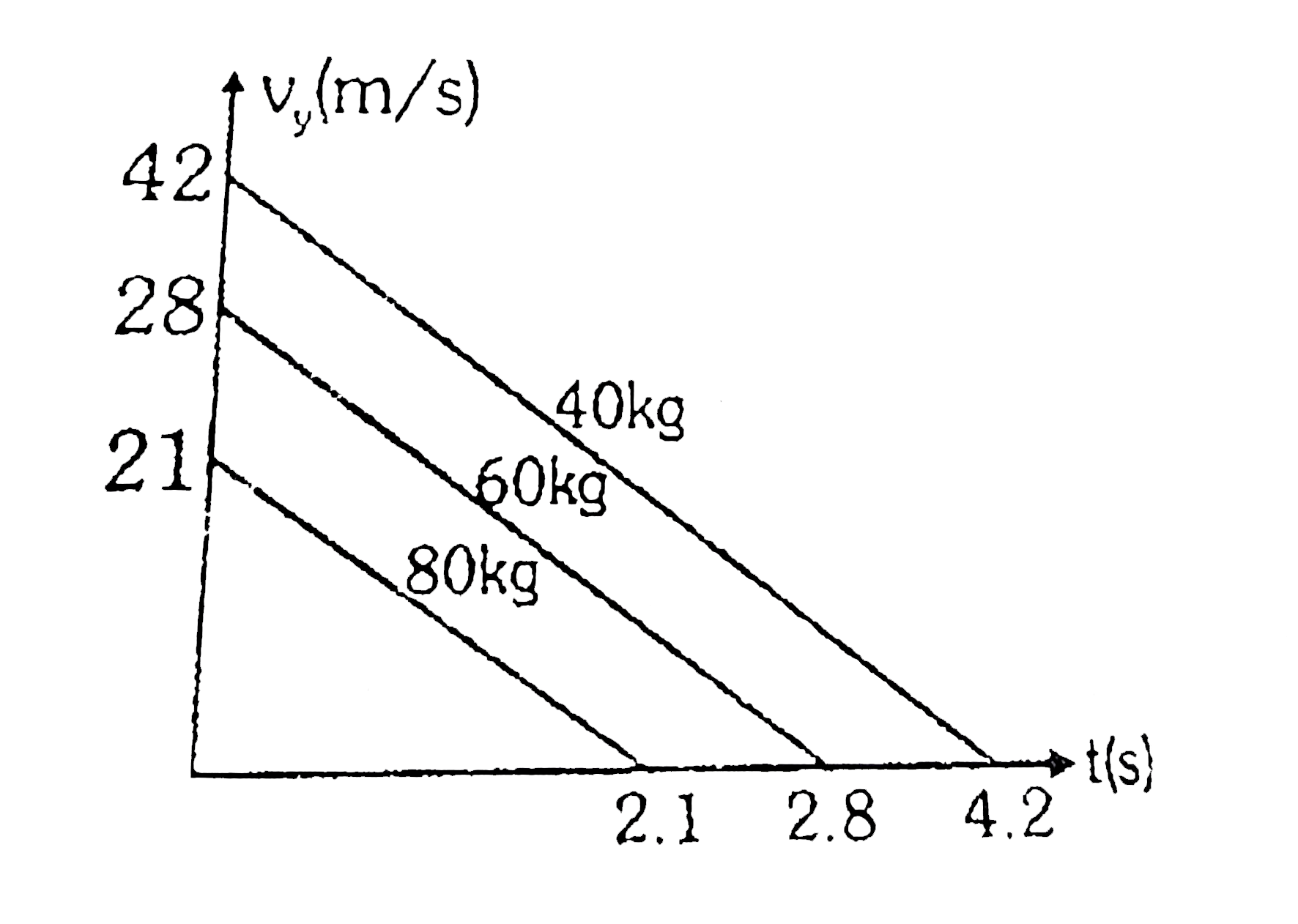
From figure 2, approximately how much time will it take for clown with a mass of 60 kg to reach the safety net located 10m below the height of the cannot?
4.3s
6.4s
5.9s
7.2s
The correct Answer is:C
Topper's Solved these Questions
- KINEMATICSBOOK - ALLENCHAPTER - KINEMATICSEXERCISE - Comprehension#6
4 Videos
- KINEMATICSBOOK - ALLENCHAPTER - KINEMATICSEXERCISE - Comprehension#7
3 Videos
- KINEMATICSBOOK - ALLENCHAPTER - KINEMATICSEXERCISE - Comprehension#4
3 Videos
- ERROR AND MEASUREMENTBOOK - ALLENCHAPTER - ERROR AND MEASUREMENTEXERCISE - Part-2(Exercise-2)(B)
22 Videos
- KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)BOOK - ALLENCHAPTER - KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)EXERCISE - BEGINNER S BOX-7
8 Videos
Similar Questions
A circus wishes to develop a new clown act. Fig. (1) shows a diagram of the proposed setup. A clown will be shot out of a cannot with velocity v0 at a trajectory that makes an angle θ=45∘ with the ground. At this angile, the clown will travell a maximum horizontal distance. The cannot will accelerate the clown by applying a constant force of 10,000N over a very short time of 0.24s. The height above the ground at which the clown begins his trajectory is 10m.
A large hoop is to be suspended from the celling by a massless cable at just the right place so that the clown will be able to dive through it when he reaches a maximum height above the ground. After passing through the hoop he will then continue on his trajectory until arriving at the safety net. Fig (2) shows a graph of the vertical component of the clown's velocity as a function of time between the cannon and the hoop. Since the velocity depends on the mass of the particular clown performing the act, the graph shows data for serveral different masses.
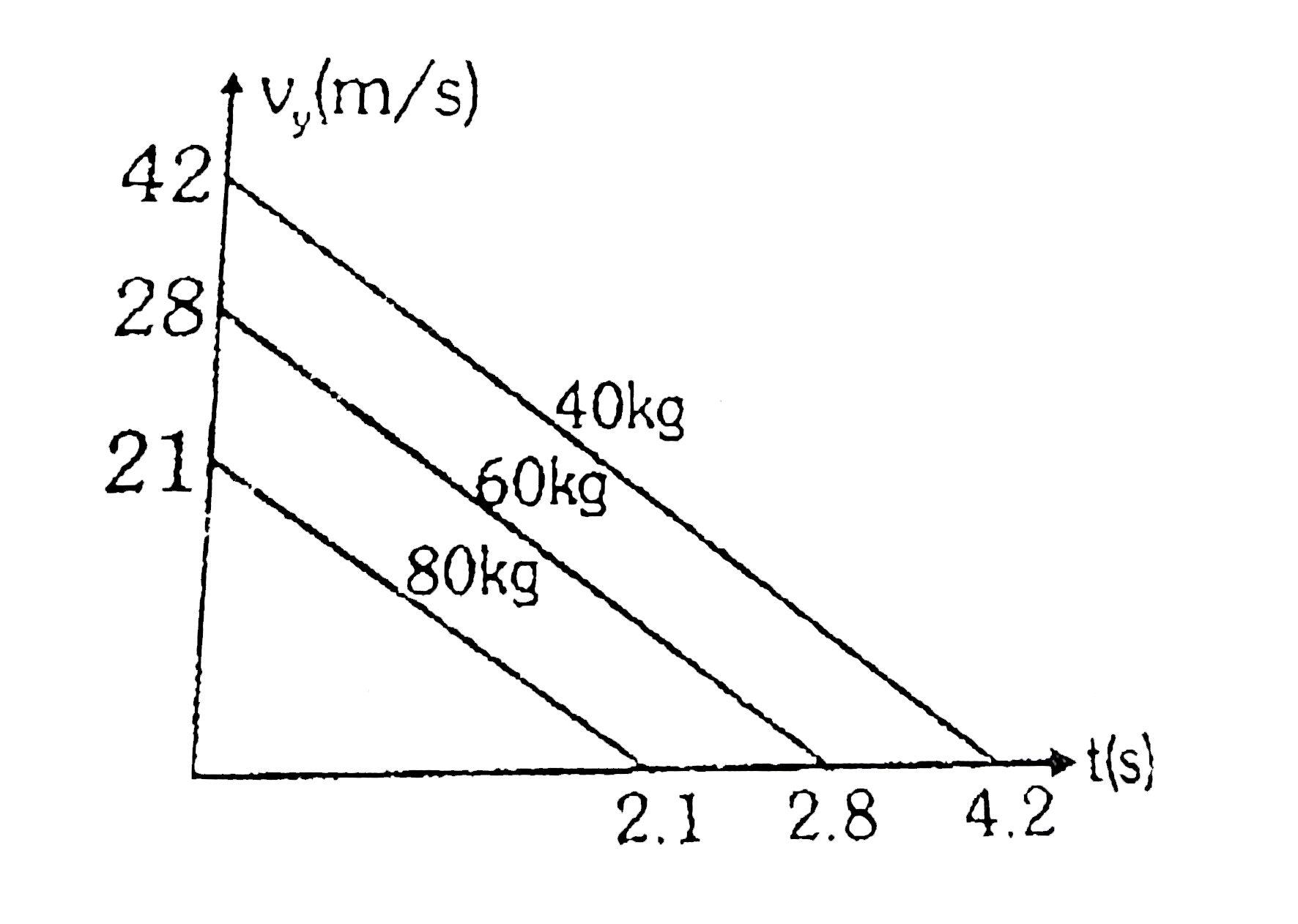
If the clown's mass is 80kg, what initial velocity v0 will have as he leaves the cannot?
View SolutionA circus wishes to develop a new clown act. Fig. (1) shows a diagram of the proposed setup. A clown will be shot out of a cannot with velocity v0 at a trajectory that makes an angle θ=45∘ with the ground. At this angile, the clown will travell a maximum horizontal distance. The cannot will accelerate the clown by applying a constant force of 10,000N over a very short time of 0.24s. The height above the ground at which the clown begins his trajectory is 10m.

A large hoop is to be suspended from the celling by a massless cable at just the right place so that the clown will be able to dive through it when he reaches a maximum height above the ground. After passing through the hoop he will then continue on his trajectory until arriving at the safety net. Fig (2) shows a graph of the vertical component of the clown's velocity as a function of time between the cannon and the hoop. Since the velocity depends on the mass of the particular clown performing the act, the graph shows data for serveral different masses.

If the mass of a clown doubles, his initial kinetic energy, mv20/2, will :-
View SolutionA circus wishes to develop a new clown act. Fig. (1) shows a diagram of the proposed setup. A clown will be shot out of a cannot with velocity v0 at a trajectory that makes an angle θ=45∘ with the ground. At this angile, the clown will travell a maximum horizontal distance. The cannot will accelerate the clown by applying a constant force of 10,000N over a very short time of 0.24s. The height above the ground at which the clown begins his trajectory is 10m.

A large hoop is to be suspended from the celling by a massless cable at just the right place so that the clown will be able to dive through it when he reaches a maximum height above the ground. After passing through the hoop he will then continue on his trajectory until arriving at the safety net. Fig (2) shows a graph of the vertical component of the clown's velocity as a function of time between the cannon and the hoop. Since the velocity depends on the mass of the particular clown performing the act, the graph shows data for serveral different masses.

If the angle the cannot makes with the horiaontal is increased from 45∘, the hoop will have to be
View SolutionA circus wishes to develop a new clown act. Fig. (1) shows a diagram of the proposed setup. A clown will be shot out of a cannot with velocity v0 at a trajectory that makes an angle θ=45∘ with the ground. At this angile, the clown will travell a maximum horizontal distance. The cannot will accelerate the clown by applying a constant force of 10,000N over a very short time of 0.24s. The height above the ground at which the clown begins his trajectory is 10m.

A large hoop is to be suspended from the celling by a massless cable at just the right place so that the clown will be able to dive through it when he reaches a maximum height above the ground. After passing through the hoop he will then continue on his trajectory until arriving at the safety net. Fig (2) shows a graph of the vertical component of the clown's velocity as a function of time between the cannon and the hoop. Since the velocity depends on the mass of the particular clown performing the act, the graph shows data for serveral different masses.

If a clown holds on to hoop instead of passing through it, what is the position of the cable so that he doesn't hit his head on the ceiling as he swings upward?
View SolutionA circus wishes to develop a new clown act. Fig. (1) shows a diagram of the proposed setup. A clown will be shot out of a cannot with velocity v0 at a trajectory that makes an angle θ=45∘ with the ground. At this angile, the clown will travell a maximum horizontal distance. The cannot will accelerate the clown by applying a constant force of 10,000N over a very short time of 0.24s. The height above the ground at which the clown begins his trajectory is 10m.

A large hoop is to be suspended from the celling by a massless cable at just the right place so that the clown will be able to dive through it when he reaches a maximum height above the ground. After passing through the hoop he will then continue on his trajectory until arriving at the safety net. Fig (2) shows a graph of the vertical component of the clown's velocity as a function of time between the cannon and the hoop. Since the velocity depends on the mass of the particular clown performing the act, the graph shows data for serveral different masses.

The slope of the line segments plotted in figure 2 is a figure constant. Which one of the following physical quantities does this slope represent?
View SolutionWhich of the following cannot be accelerated by applying an electric field?
View SolutionA particle is projected from the ground with velocity u making an angle θ with the horizontal. At half of its maximum heights,
View SolutionA shot is fired at an angle θ to the horizontal such that it strikes the hill while moving horizontally. Find the initial angle of projection θ.
View SolutionA : It is not possible to have constant velocity and variable acceleration.
R : Accelerated body cannot have constant velocity.
View SolutionA particle is projected at an angle θ=30∘ with the horizontal, with a velocity of 10ms−1. Then
View Solution

