A particle is projected at an angle θ=30∘ with the horizontal, with a velocity of 10ms−1. Then
After 2 s, the velocity of particle makes an angle of 60∘ with initial velocity vector.
After 1 s, the velocity of particles makes an angle of 60∘ with initial velocity vector.
The magnitude of velocity of particle after 1 s is 10ms−1.
The magnitude of velocity of particle after 1 s is 5ms−1.
The correct Answer is:B, C
To solve the problem step by step, we will analyze the motion of the particle projected at an angle of θ=30∘ with an initial velocity of 10m/s.
Step 1: Determine the Initial Velocity Components
The initial velocity →v0 can be broken down into its horizontal and vertical components using trigonometric functions:
- v0x=v0cos(θ)
- v0y=v0sin(θ)
Given:
- v0=10m/s
- θ=30∘
Calculating the components:
- v0x=10cos(30∘)=10×√32=5√3m/s
- v0y=10sin(30∘)=10×12=5m/s
Thus, the initial velocity vector is:
→v0=5√3^i+5^j
Step 2: Determine the Velocity After 1 Second
The horizontal component of the velocity remains constant throughout the motion:
vx=v0x=5√3m/s
The vertical component of the velocity changes due to gravity:
vy=v0y−gt
Where g=10m/s2 (acceleration due to gravity) and t=1s:
vy=5−10×1=5−10=−5m/s
Thus, the velocity vector after 1 second is:
→v=5√3^i−5^j
Step 3: Calculate the Magnitude of the Velocity After 1 Second
The magnitude of the velocity vector is given by:
|→v|=√v2x+v2y
Substituting the values:
|→v|=√(5√3)2+(−5)2=√75+25=√100=10m/s
Step 4: Determine the Angle Between Initial and Final Velocity Vectors
To find the angle θ between the initial and final velocity vectors, we use the dot product:
cos(θ)=→v0⋅→v|→v0||→v|
Calculating the dot product:
→v0⋅→v=(5√3)(5√3)+(5)(−5)=75−25=50
The magnitudes are:
- |→v0|=10m/s
- |→v|=10m/s
Thus,
cos(θ)=5010×10=50100=0.5
Therefore,
θ=cos−1(0.5)=60∘
Conclusion
After 1 second, the velocity of the particle makes an angle of 60∘ with the initial velocity vector, and the magnitude of the velocity after 1 second is 10m/s.
The initial velocity →v0 can be broken down into its horizontal and vertical components using trigonometric functions:
- v0x=v0cos(θ)
- v0y=v0sin(θ)
- v0=10m/s
- θ=30∘
- v0x=10cos(30∘)=10×√32=5√3m/s
- v0y=10sin(30∘)=10×12=5m/s
→v0=5√3^i+5^j
The horizontal component of the velocity remains constant throughout the motion:
vx=v0x=5√3m/s
vy=v0y−gt
Where g=10m/s2 (acceleration due to gravity) and t=1s:
vy=5−10×1=5−10=−5m/s
→v=5√3^i−5^j
The magnitude of the velocity vector is given by:
|→v|=√v2x+v2y
Substituting the values:
|→v|=√(5√3)2+(−5)2=√75+25=√100=10m/s
To find the angle θ between the initial and final velocity vectors, we use the dot product:
cos(θ)=→v0⋅→v|→v0||→v|
→v0⋅→v=(5√3)(5√3)+(5)(−5)=75−25=50
- |→v0|=10m/s
- |→v|=10m/s
cos(θ)=5010×10=50100=0.5
Therefore,
θ=cos−1(0.5)=60∘
After 1 second, the velocity of the particle makes an angle of 60∘ with the initial velocity vector, and the magnitude of the velocity after 1 second is 10m/s.
Topper's Solved these Questions
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Linked Comprehension Type
35 Videos
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Integer Type
17 Videos
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Interger type
3 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Single correct anwer type
14 Videos
- MISCELLANEOUS VOLUME 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - INTEGER_TYPE
10 Videos
Similar Questions
A ball is projected at an angle 30° with the horizontal with the velocity 49ms−1. The horizontal range is
View SolutionA particle of mass 1 kg is projected at an angle of 30∘ with horizontal with velocity v = 40 m/s . The change in linear momentum of the particle after time t = 1 s will be (g = 10 m/s2)
View Solution
Knowledge Check
If a body is projected with an angle θ to the horizontal, then
Aits velocity is always perpendicular to its acceleration thenBits velocity becomes zero at its maximum height.Cits velocity makes zero angle with the horizontal at its maximum height.Dthe body just before hitting the ground, the direction of velocity coincides with the acceleration.
In a region , an electroc field E=10NC−1 making an angle of θ=30∘ with the horizontal plane is present. Coefficient of restitution between ball and surface is e=0.2. Ball has charge q=−2C over it and mass m = 2 kg . Ball is projected at an angle of θ=30∘ with the horizontal with speed u=10ms−1
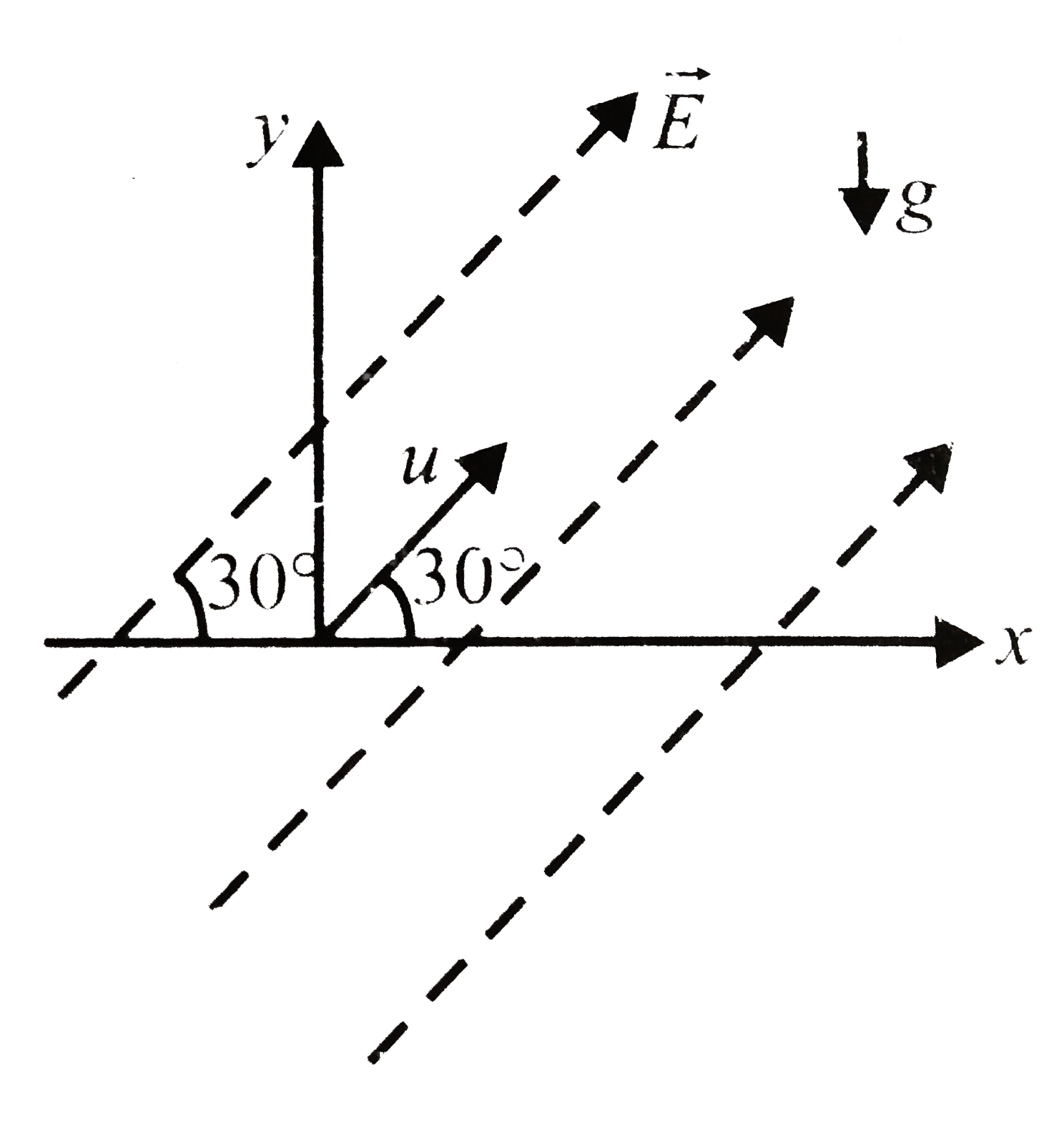
Horizontal distance traveled up to first rebound is
View SolutionA body is projected at an angle of 30∘ with the horizontal and with a speed of 30ms−1. What is the angle with the horizontal after 1.5s ? (g=10ms−2).
View SolutionA particle is projected at an angle of 60∘ above the horizontal with a speed of 10m/s. After some time the direction of its velocity makes an angle of 30∘ above the horizontal. The speed of the particle at this instant is
View SolutionA particle of mass 1kg is projected at an angle of θ=π/4 from horizontal with a muzzle velocity of 20m/s. A long slender rod of mass 5kg and length 30m is suspended vertically from a point at the same horizontal leves as that of point of projection and at a distance of 60m from the projection point. The rod can rotate freely. If collision occurs, it is perfectly plastic. (g=10m/s2)
If the rod tilts to an angle θ after collision, then
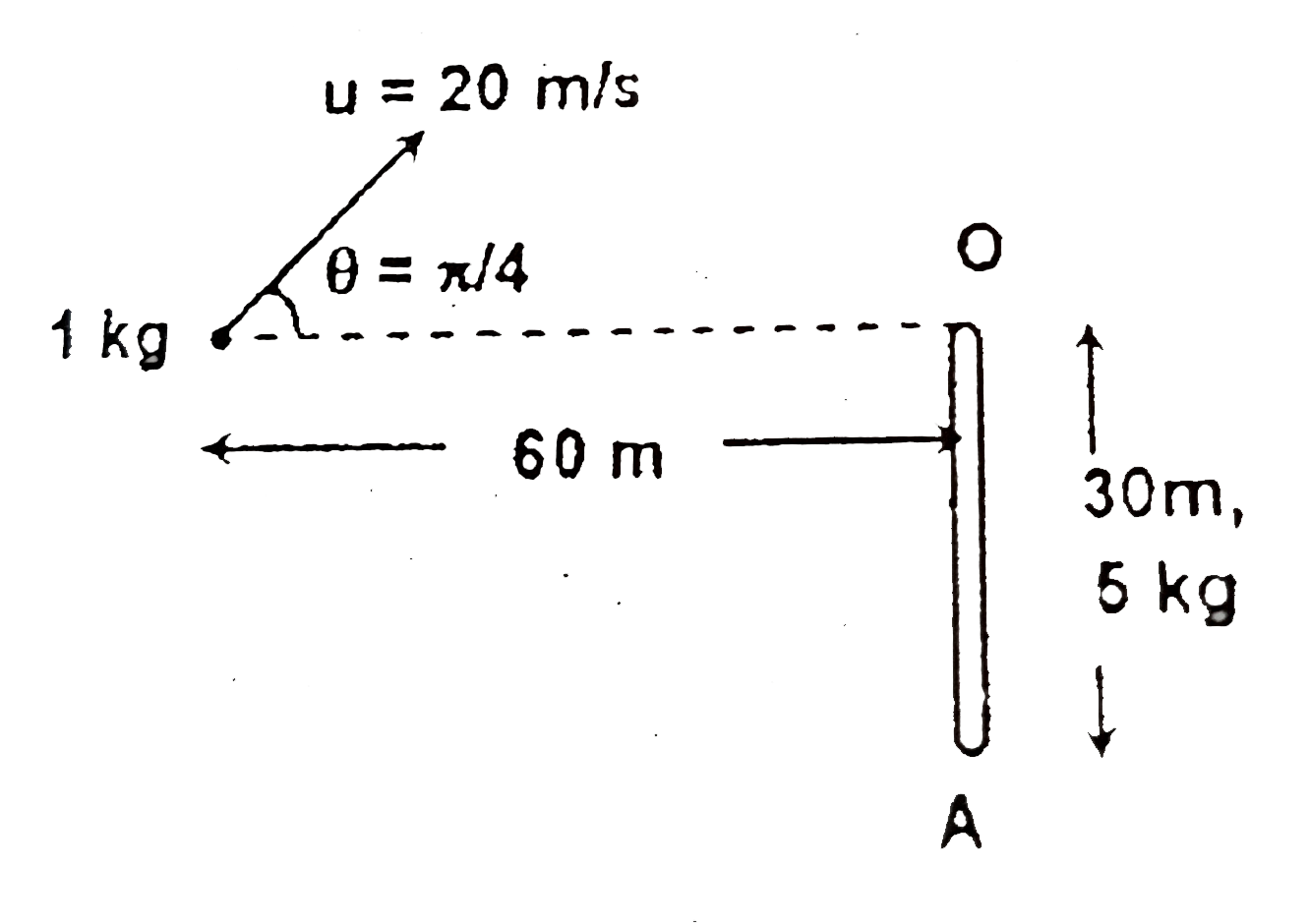
View SolutionA particle of mass 1kg is projected at an angle of θ=π/4 from horizontal with a muzzle velocity of 20m/s. A long slender rod of mass 5kg and length 30m is suspended vertically from a point at the same horizontal leves as that of point of projection and at a distance of 60m from the projection point. The rod can rotate freely. If collision occurs, it is perfectly plastic. (g=10m/s2)
Angular velocity of rod after collision is
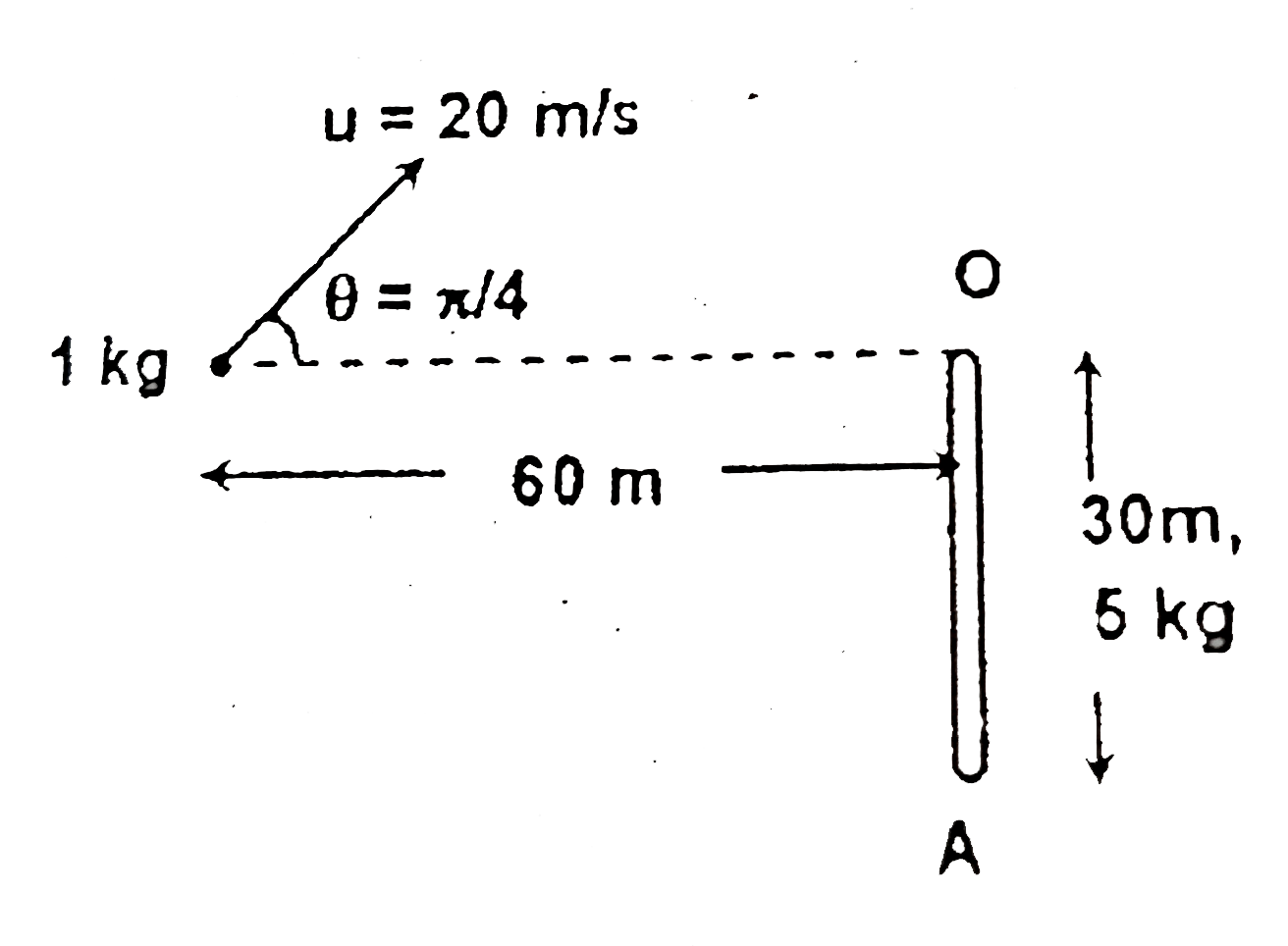
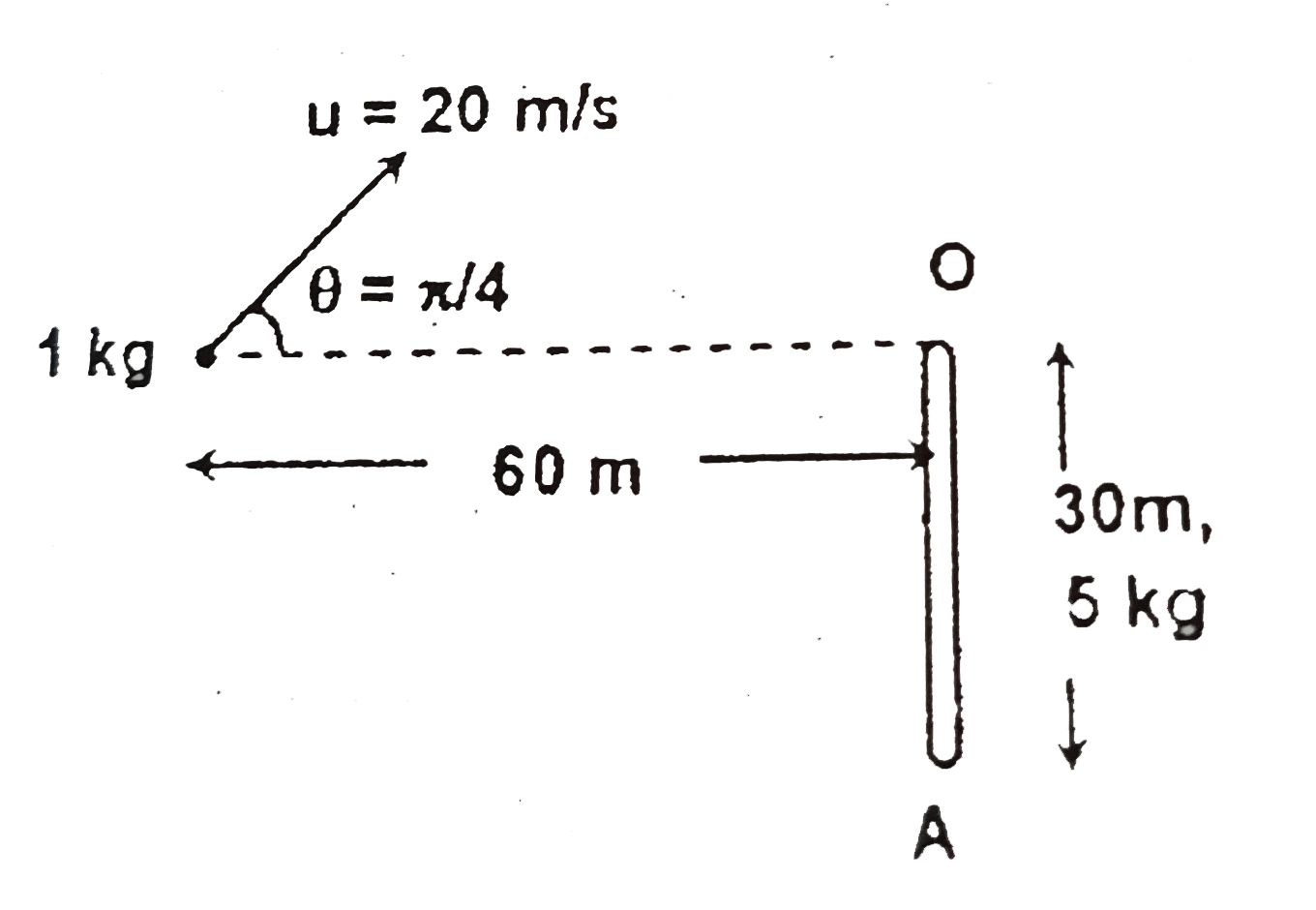
View SolutionA particle of mass 1kg is projected at an angle of θ=π/4 from horizontal with a muzzle velocity of 20m/s. A long slender rod of mass 5kg and length 30m is suspended vertically from a point at the same horizontal leves as that of point of projection and at a distance of 60m from the projection point. The rod can rotate freely. If collision occurs, it is perfectly plastic. (g=10m/s2)
If projectile is fired horizontally, it will
View SolutionWhat is the radius of curvature of the parabola traced out by the projectile in which a particle is projected with a speed u at an angle θ with the horizontal, at a point where the velocity of particle makes an angle θ/2 with the horizontal.
View Solution
