S in any point on side QR of a ΔPQR.ShowtˆPQ + QR+RP gt 2PS.
Video Solution
Text Solution
Given in ΔPQR,S is any point on side QR .
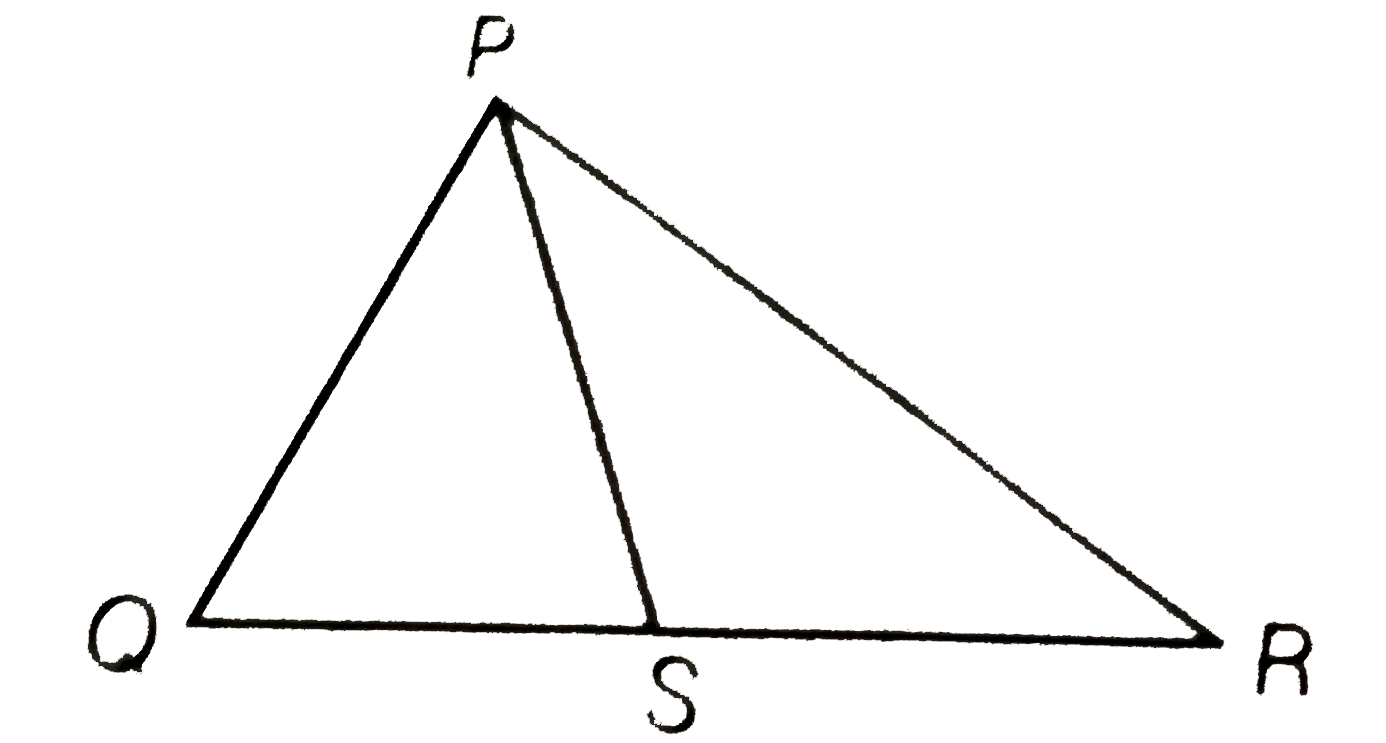
To show PQ+QR+RP>2PS
Proof In ΔPQS. PQ+QS>2PS ……(i)
[sum of two sides of a triangle is grater then the third side ]
Simiarly∈ SR+RP>PS ...(ii)
[Sum of two sides of a triangle is greater then the third side ]
On adding Eqs.(i) and (ii) we get
PQ+QS+SR+RP>2PS
⇒ PQ+(QS+SR)+RP>2PS
⇒ PQ+QR+RP>2PS [∵QR=QS+SR]
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
If S is any point on the side QR of a ΔPQR, then
APQ+QR+RP>2PSBPQ+QR+RP<2PSCPQ+QR+RP=3PSDNone of theseS and U are two points on the side PQ of ΔPQR , such that QU=PS . If ST||QR and UV∣∣PR , then
ATV||PQBTV⊥PQCTV and PQ intersect at 60∘DTV and PQ intersect at 45∘
If S is a point on side PQ of a △PQR such that PS = QS = RS, then PR2+QR2 = ……………..
View SolutionIf S is the mid-point of side QR of a ΔPQR, then prove that PQ+PR=2PS.
View SolutionIn PQR , S is any point on the side QR . Show that PQ+QR+RP>2PS
View SolutionS and T are points on sides PR and QR of ΔPQRsuch that ∠P=∠RTS. Show that ΔRPQ~ΔRTS.
View SolutionS and T are points on sides PR and QR of ΔPQR such that ∠P=∠RTS Show that ΔRPQ~ΔRTS
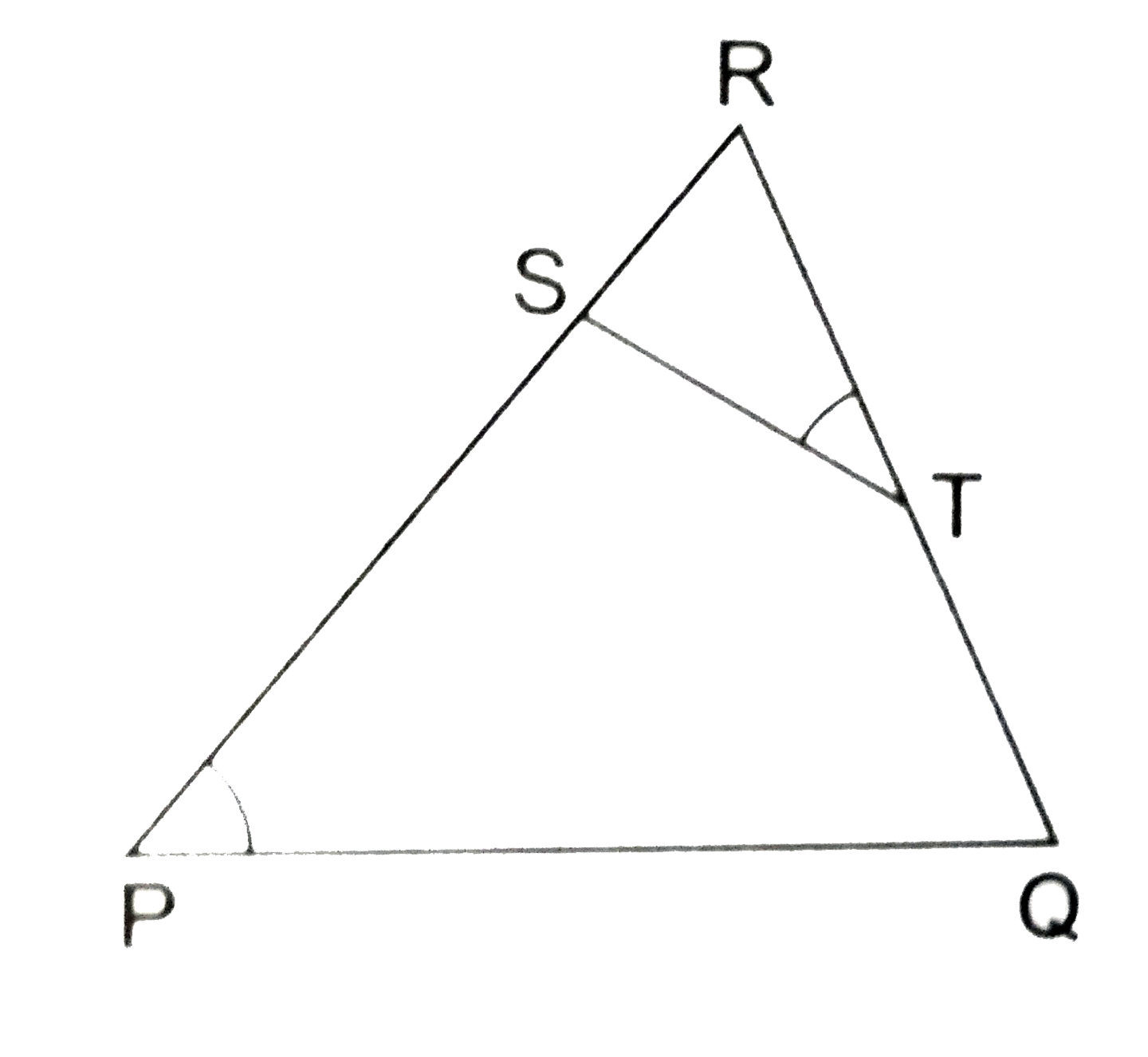
View SolutionIn the given figure, S and T are points on sides PR and QR of ΔPQR such that ∠P=∠RTS. Show that ΔRPQ~ΔRTS.
View Solution
