Show that in a quadrilateral ABCD ,AB+BC+CD+DA<2(BD+AC)
To prove that in a quadrilateral ABCD, the inequality AB+BC+CD+DA<2(BD+AC) holds, we can follow these steps:
1. Construct the Quadrilateral:
Begin by sketching the quadrilateral ABCD. Label the vertices A, B, C, and D.
2. Introduce a Point O:
Choose a point O inside the quadrilateral ABCD. This point will help us divide the quadrilateral into triangles.
3. Form Triangles:
From point O, draw segments to each vertex of the quadrilateral. This will create four triangles: AOB, BOC, COD, and DOA.
4. Apply Triangle Inequality:
For each triangle, apply the triangle inequality:
- In triangle AOB:
AB<OA+OB
- In triangle BOC:
BC<OB+OC
- In triangle COD:
CD<OC+OD
- In triangle DOA:
DA<OD+OA
5. Add the Inequalities:
Now, add all these inequalities together:
AB+BC+CD+DA<(OA+OB)+(OB+OC)+(OC+OD)+(OD+OA)
Simplifying the right-hand side gives:
AB+BC+CD+DA<2(OA+OB+OC+OD)
6. Relate to Diagonals:
Notice that the segments OA, OB, OC, and OD can be rearranged to relate to the diagonals BD and AC. Specifically, we can express:
OA+OC=ACandOB+OD=BD
Thus, we can rewrite:
OA+OB+OC+OD=AC+BD
7. Final Inequality:
Substitute this back into the inequality:
AB+BC+CD+DA<2(OA+OB+OC+OD)=2(AC+BD)
Therefore, we conclude:
AB+BC+CD+DA<2(BD+AC)
Conclusion:
We have shown that in quadrilateral ABCD, the inequality AB+BC+CD+DA<2(BD+AC) holds true.
Begin by sketching the quadrilateral ABCD. Label the vertices A, B, C, and D.
Choose a point O inside the quadrilateral ABCD. This point will help us divide the quadrilateral into triangles.
From point O, draw segments to each vertex of the quadrilateral. This will create four triangles: AOB, BOC, COD, and DOA.
For each triangle, apply the triangle inequality:
- In triangle AOB:
AB<OA+OB
- In triangle BOC:
BC<OB+OC
- In triangle COD:
CD<OC+OD
- In triangle DOA:
DA<OD+OA
Now, add all these inequalities together:
AB+BC+CD+DA<(OA+OB)+(OB+OC)+(OC+OD)+(OD+OA)
Simplifying the right-hand side gives:
AB+BC+CD+DA<2(OA+OB+OC+OD)
Notice that the segments OA, OB, OC, and OD can be rearranged to relate to the diagonals BD and AC. Specifically, we can express:
OA+OC=ACandOB+OD=BD
Thus, we can rewrite:
OA+OB+OC+OD=AC+BD
Substitute this back into the inequality:
AB+BC+CD+DA<2(OA+OB+OC+OD)=2(AC+BD)
Therefore, we conclude:
AB+BC+CD+DA<2(BD+AC)
We have shown that in quadrilateral ABCD, the inequality AB+BC+CD+DA<2(BD+AC) holds true.
Topper's Solved these Questions
Similar Questions
Show that in a quandrilateral ABCD,AB+BC+CD+DA<2(BD+AC).
View SolutionShow that in a quadrilateral ABCD AB+BC+CD+DA>AC+BD
View SolutionIn a quadrilateral ABCD, show that (AB+BC+CD+DA)<2(BD+AC).
View SolutionIn a quadrilateral ABCD, show that
(AB+BC+CD+DA)>(AC+BD).
View SolutionIn quadrilatcal ABCD, prove that AB+BC+CD+AD<2(BD+AC)
View SolutionABCD is quadrilateral. Is AB+BC+CD+DA<2(AC+BD)?
View SolutionABCD is a quadrilateral. Is AB+BC+CD+DA>AC+BD?
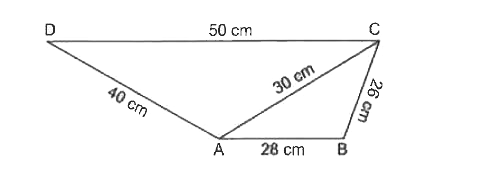
View SolutionIn a quadrilateral ABCD, AB = 28 cm, BC = 26 cm, CD = 50 cm, DA = 40 cm and diagonal AC = 30 cm. Find the area of the quadrilateral.
View SolutionIn cyclic quadrilateral ABCD, AD∣∣BC. Prove that AB = CD.
View SolutionThe given figure shows a quadrilateral ABCD. Prove that :
AB+BC+CD+DA>AC+BD

View Solution
