In a quadrilateral ABCD, AB = 28 cm, BC = 26 cm, CD = 50 cm, DA = 40 cm and diagonal AC = 30 cm. Find the area of the quadrilateral.
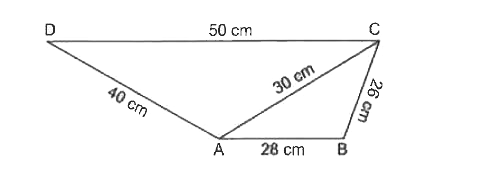
The correct Answer is:936cm2
Step by step video, text & image solution for In a quadrilateral ABCD, AB = 28 cm, BC = 26 cm, CD = 50 cm, DA = 40 cm and diagonal AC = 30 cm. Find the area of the quadrilateral. by Maths experts to help you in doubts & scoring excellent marks in Class 7 exams.
Updated on:21/07/2023Topper's Solved these Questions
- MENSURATIONBOOK - RS AGGARWALCHAPTER - MENSURATIONEXERCISE - EXERCISE 20E
21 Videos
- MENSURATIONBOOK - RS AGGARWALCHAPTER - MENSURATIONEXERCISE - EXERCISE 20F
16 Videos
- MENSURATIONBOOK - RS AGGARWALCHAPTER - MENSURATIONEXERCISE - EXERCISE 20C
16 Videos
- LINES AND ANGLESBOOK - RS AGGARWALCHAPTER - LINES AND ANGLESEXERCISE - Exercise 13
11 Videos
- PERCENTAGE BOOK - RS AGGARWALCHAPTER - PERCENTAGE EXERCISE - TEST PAPER
16 Videos
Similar Questions
Knowledge Check
A park is in the shape of quadrilateral ABCD in which AB=9cm,BC=12cm,CD=5cm,AD=8cm and ∠C=90∘. Find the area of the park.
A65.4cm2B69.4cm2C66.4cm2D68.4cm2The base of a right prism is a quadrilateral ABCD. Given that AB = 9 cm, BC = 14 cm, CD = 13 cm, DA = 12 cm and ∠DAB=90∘. If the volume of the prism be 2070cm3, then the area of the lateral surface is
A720cm2B810cm2C1260cm2D2070cm2
Construct a quadrilateral ABCD given that AB=5cm, BC=4cm, CD=4.5cm, DA=3cm and diagonal AC=4cm.
View SolutionIs it possible to construct a quadrilateral ABCD in which AB = 3 cm, BC = 4 cm, CD = 5.4 cm, DA = 5.9 cm and diagonal AC = 8 cm? If not, why?
View SolutionConstruct as quadrilateral ABCD in which AB=4.8cm, BC=4.3cm, CD=3.6cm, AD=4.2cm and diagonal AC=6cm.
View SolutionConstruct a quadrilateral ABCD in which AB =4.6 cm , BC=2.6 cm, CD=3.5 cm, AD=2.6 cm , and the diagonal AC=4.9 cm.

View SolutionFind the area of the quadrilateral ABCD in which in AB = 42 cm, BC = 21 cm, CD = 29 cm, DA = 34 cm and diagonal BD = 20 cm.
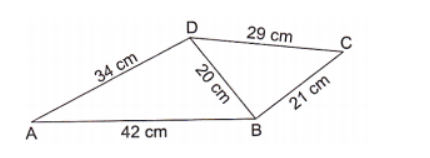
View SolutionConstruct a quadrilateral ABCD in which AB = 4 . 6 cm, BC = 2.6 cm, CD = 3.5 cm AD = 2 . 6 cm, and the diagonal AC = 4 . 9 cm

View Solution
