Prove that sum of any two sides of a triagle is greater than twice the median with respect to the third side.
Given in ΔABC ,AD is a median
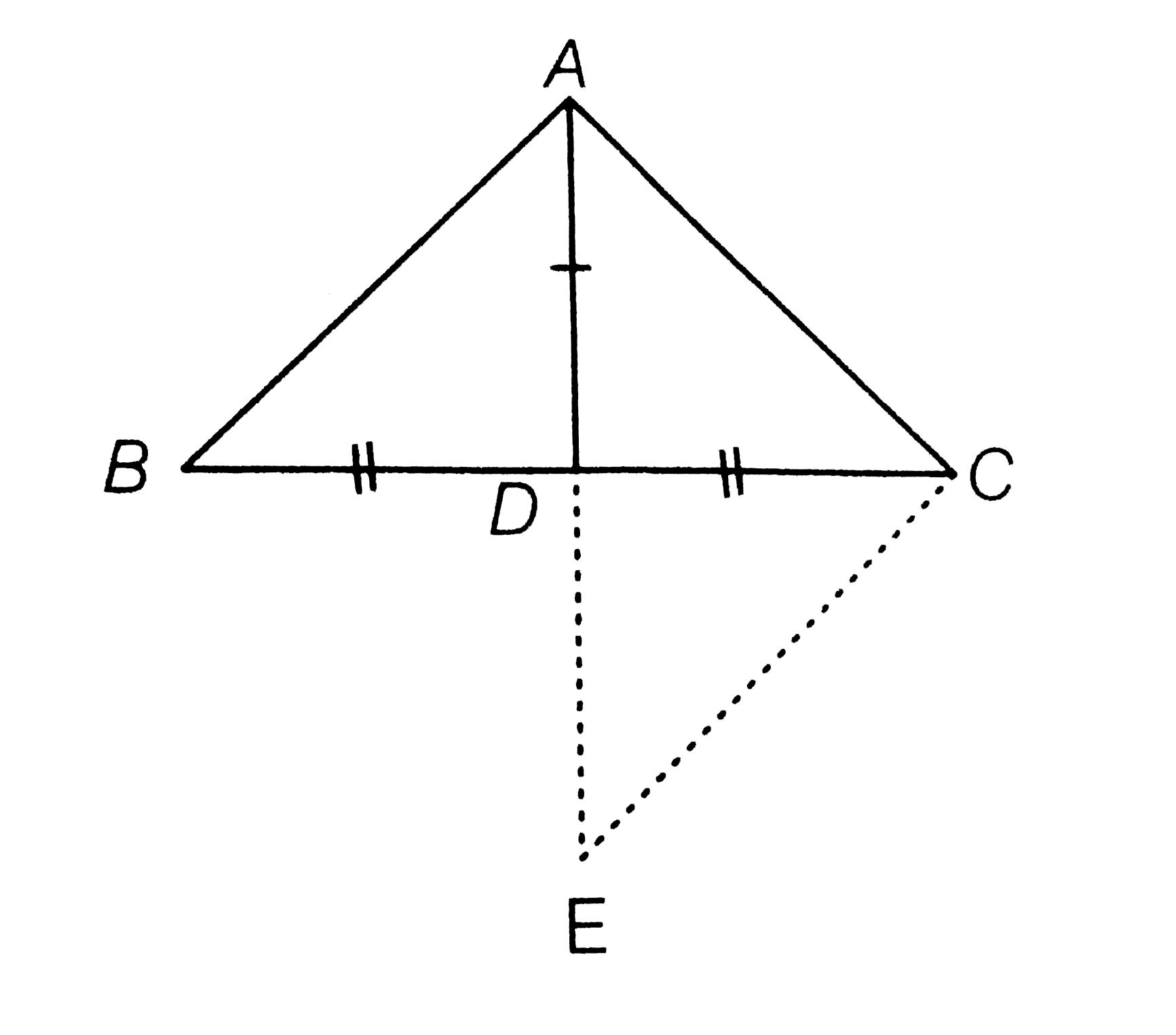
Constrution
Produce AD to a point E such that AD=DE and join CE
TP prove AC+AB>2AD
Proof in ΔABDandΔECD
AD =DE [by construction ]
BD =CD [given AD is the median ]
a∩g≤ADB=∠CDE [vertically opposite angle ]
∴ΔABD≅ΔECD [by SAS congruence rule ]
⇒AB=CE [by CPCT ]
Now in ΔAEC,
AC+EC>AE [Sum of two sides of a triagle is grater than the third side ]
∴AC+AB>2AD [from Eq. (i) and also taken that AD=AE ]
Topper's Solved these Questions
Similar Questions
Prove that sum of any two sides of a triangle is greater than twice the median with respect to the third side.
View SolutionProve that sum of any two medians of a triangle is greater than the third median.
View SolutionSum of any two sides of a triangle is greater than the third side.
View SolutionThe sum of any two sides of a triangle is greater than third side.
View SolutionProve that the sum of any two sides of a triangle is greater than two times the median of third side.
View SolutionWhich of the following statements are true (T) and which are false (F)? Sum of the three sides of a triangle is less than the sum of its three altitudes. Sum of any two sides of a triangle is greater than twice the median drawn to the third side. Sum of any two sides of a triangle is greater than the third side. Difference of any two sides of a triangle is equal to the third side. If two angles of a triangle are unequal, then the greater angle has the larger side opposite to it. Of all the line segments that can be drawn from a point to a line not containing it, the perpendicular line segment is the shortest one.
View SolutionProve that any two sides of a triangle are together greater than twice the median drawn to the third side. GIVEN : ABC in which AD is a median. PROVE : AB+AC>2AD CONSTRUCTION : Produce AD to E such that AD=DE. Join EC.
View SolutionProve that any two sides of a triangle are together greater than twice the median drawn to the third side.
View SolutionProperty The sum of any two sides of a triangle is greater than the third side.
View SolutionSum of any two sides of a triangle is not less than the third side
View Solution
