ΔABC is a right triangle right angled at A such that AB=AC and bisector of ∠C intersects the side AB at D. Prove that AC+AD=BC.
Video Solution
Text Solution
Given in right angled ΔABC AB=AC and CD is the bisector of ∠C
Construction Draw DE⊥BC.
To prove AC+AD=BC
Proof In right angled ΔABC,AB =AC and BC is a hpotenuse [given]
∴∠A90∘
In ΔDACandΔDEC ∠A=∠3=90∘
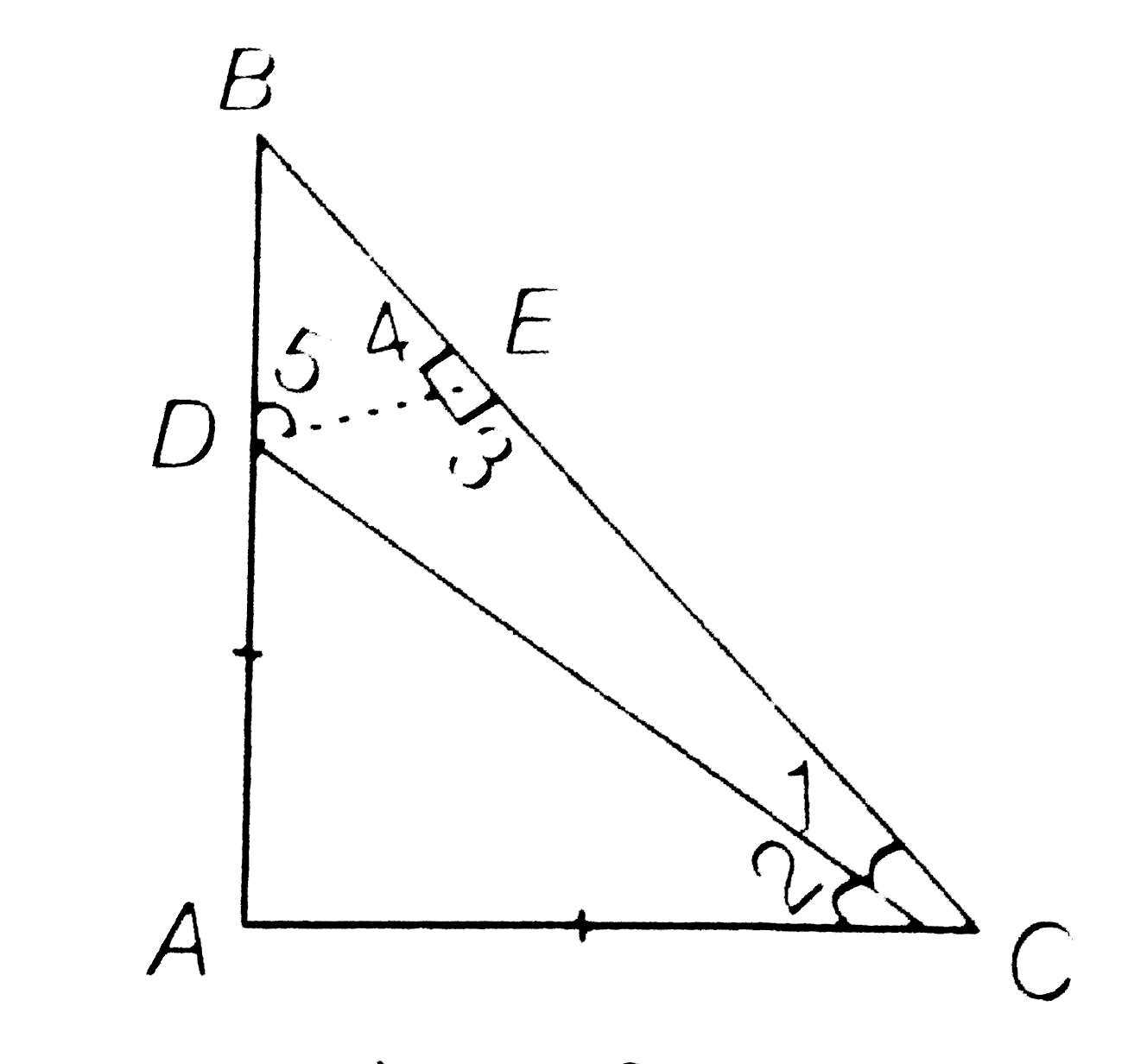
∠1=∠2 [given ,CD is the bisector of ∠C ]
DC=DC [common sides]
therforeΔDAC≅ΔDEC [by AAS cogruence rule ]
⇒DA=DE [ by CPCT ] ....(i)
and AC =EC ...(ii)
In ΔABCAB=AC
∠C=an≥lB
[angle opposite to equal sides are equal ] ...(iii)
Again in ΔABC∠A+an≥lB+an≥lC=180∘
[by angle sum property of a triangel ]
⇒90∘+∠B+an≥lB=180∘
⇒2an≥lB=180∘−90∘
⇒2∠B=90∘
⇒∠B=45∘
in ΔBED∠5=180∘−(∠B+an≥l4)
[by angle sum property of a triangle ]
=180∘−(45∘+90∘
=180∘−135∘=45∘
∴∠B=ag≠l5
⇒DE=BE[∵ sides opposite to equal angles are equal ]
In From Eqs. (i) and (iv)
DA=DE=BE
BC=CE +EB
=CA +DA [from Eqs (ii) and (V)]
∴AD+AC=BC
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
ΔABC is a right triangle , right angled at A and AD⊥BC . If AB= c and AC = b, then AD is equal to
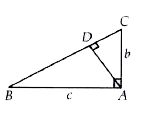 Abc√b2+c2Bbcb2+c2Cb2c√b2+c2DNone of these
Abc√b2+c2Bbcb2+c2Cb2c√b2+c2DNone of theseABC is a right-angled triangle, right angled at A and AD is the altitude on BC. If AB : AC= 3:4, what is the ratio BD:DC?
A3:4B9:16C2:3D1:2
ABC is an isosceles right triangle right-angled at C . Prove that AB2=2AC2 .
View SolutionΔABD is a right triangle, right-angled at A and AC⊥BD. Prove that AB2=BC×BD.
View SolutionABC is an isosceles right triangle, right-angled at C . Prove that: AB2=2AC2.
View SolutionABC is a isosceles right angled triangle, right angled at C. prove that AB2=2AC2
View SolutionABC is a triangle right angled at B. D is a point on AC such that ∠ABD=45∘ If AC=6 and AD=2 then AB=
View SolutionABC is a right triangle with AB = AC.If bisector of ∠A meet BC at D then prove that BC =2 AD .
View Solution

