Show that in a quadrilateral ABCD AB+BC+CD+DA>AC+BD
Given ABCD is a quadrilateral
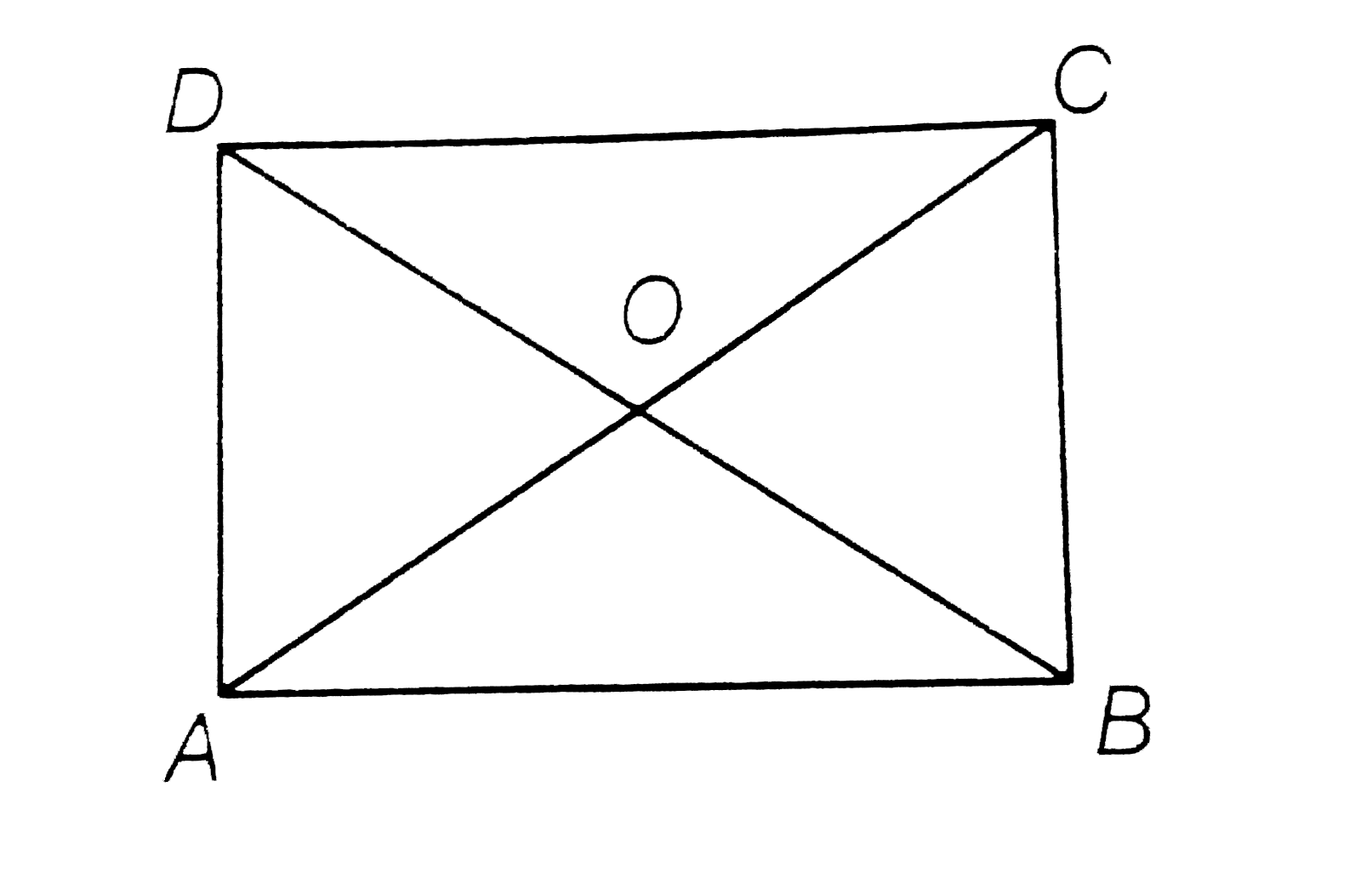
Construction
join diagonals AC and BD
To show AB+BC+CD+DA>AC+BD
In ΔABC,AB+BC>AC ...(i)
[sum of two sides of a triangle is greater than the third side]
In ΔBCD ....(ii) [sum of two sides of a triangle is greater than the third side]
In ΔCDA, CD+DA>AC ...(iii)
[sum of two sides of a triangle is greater than the third side]
In ΔDAB DA+AB>BD ....(iv)
[sum of two sides of a triangle is greater than the third side]
On adding Eqs,(i),(ii),(iii) and (iv), we get
2(AB+BC+CD+DA)>2(AC+BD)
⇒ AB+BC+CD+DA>AC+BD
Topper's Solved these Questions
Similar Questions
Show that in a quandrilateral ABCD,AB+BC+CD+DA<2(BD+AC).
View SolutionShow that in a quadrilateral ABCD ,AB+BC+CD+DA<2(BD+AC)
View SolutionThe given figure shows a quadrilateral ABCD. Prove that :
AB+BC+CD+DA>AC+BD

View SolutionIn a cyclic quadrilateral ABCD, AB = BC, AD = DC, AC⊥BD,∠CAD=θ. Then ∠ABC will be-
View SolutionIf O is a point within a quadrilateral ABCD, show that OA+OB+OC+OD>AC+BD.
View SolutionIn a quadrilateral ABCD, show that
(AB+BC+CD+DA)>(AC+BD).
View SolutionABCD is a quadrilateral. Is AB+BC+CD+DA>AC+BD?
View SolutionIn a quadrilateral ABCD, AB= AD and CB = CD, prove that AC is perpendicular bisector of BD.
View SolutionIn quadrilateral ABCD, BA = BC and DA = DC. Prove that BD bisects ∠ ABC as well as ∠ ADC.
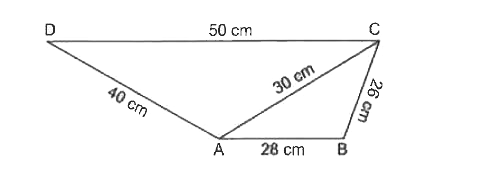
View SolutionIn a quadrilateral ABCD, AB = 28 cm, BC = 26 cm, CD = 50 cm, DA = 40 cm and diagonal AC = 30 cm. Find the area of the quadrilateral.
View Solution
