O is a point in the interior of a square ABCD such that is an equilateral triangle . Show that is an isoceles triangle .
Video Solution
Text Solution
Given O is a point in the interior of a square ABCD such that is an equilateral triangle .

Construction join OC and OD
To show is an isosceles trianlge
Proof Since,AOB is an isosceles triangle .
Also
i.e
in
AO=BO [given ]
[all the side of an equilateral triangle are equal ]
[proved above ]
and AD=BC [side of a square are equal ]
[by SAS congruence rule ]
Hence OD=OC [by CPCT ]
OC=OD
Hence is an isosceles triangle
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
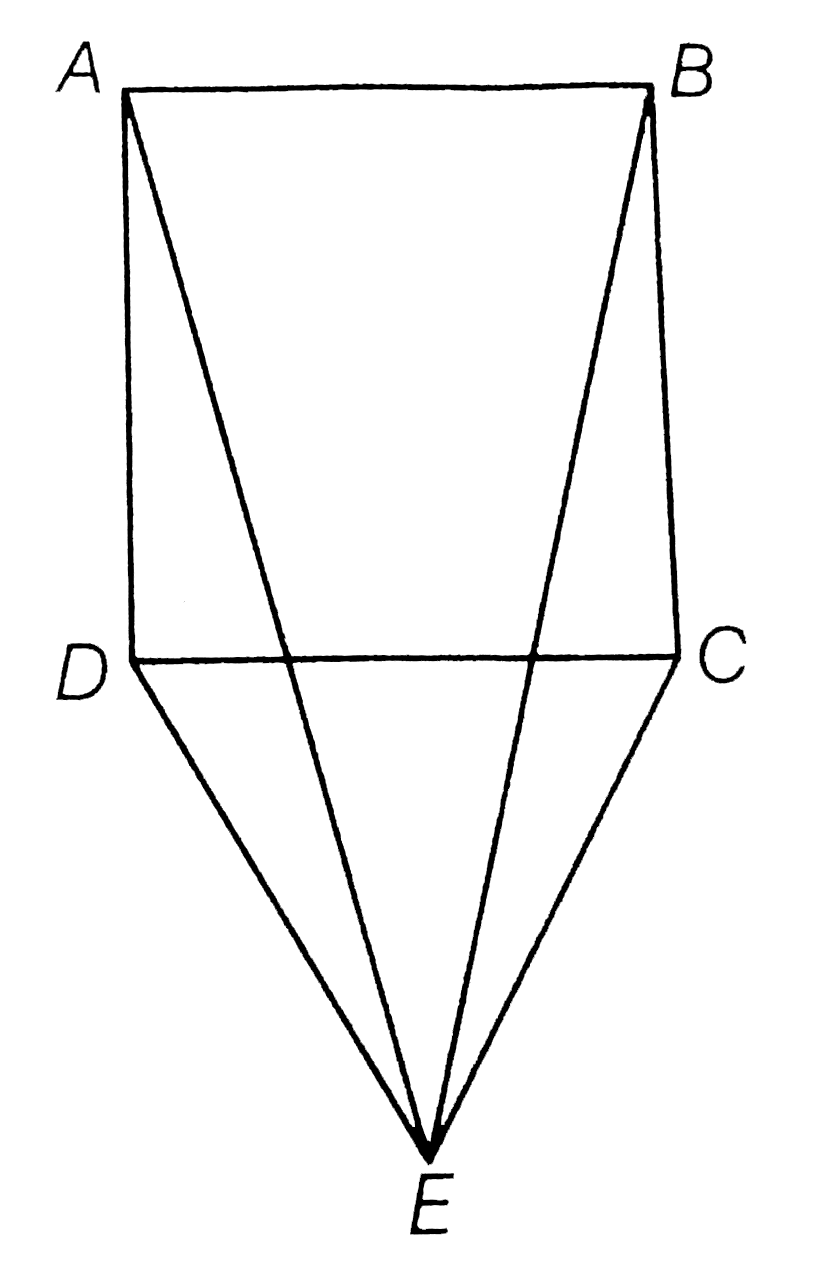
In the given figure,ΔCDE is an equlatel triangle triangle formed on a side CD of a square ABCD.Show that ΔADE≅ΔBCE.
 ARHSBSSSCAASDSAS
ARHSBSSSCAASDSASABCD is a square of side 4 cm. If E is a point in the interior of the square such that △CED is equilateral, then find the area of △ACE (in cm2).
A2(√3−1)B4(√3−1)C6(√3−1)D8(√3−1)ABCD is a square and ABE is an equilateral triangle outside the square then
A∠ACE=12∠ABEB∠ACE=∠ABEC∠ACE=2∠ABEDNone of these
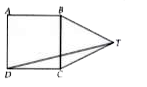
In the given figure, ABCD is a square and ΔBCT is an equilateral triangle. Find ∠BTD.
View SolutionThe given figure shows a square ABCD and an equilateral triangle ABP Calculate
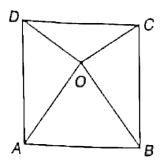
View SolutionInside a square ABCD, ΔBEC is an equilateral triangle. If CE and BD interesect at O, then ∠BOC is equal to
View SolutionABCD is a square and AOB is an equilateral triangle. What is the value of ∠DOC?
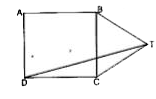
View SolutionIn the given diagram, ABCD is a square and Δ BCT is an equilateral triangle. ∠ BTD equals
View Solution
